基于粒子群算法的超临界机组给水系统模型辨识

卢晓玲，马平

（河北省发电过程仿真与优化控制工程技术研究中心（华北电力大学），河北保定 071003）

基于粒子群算法的超临界机组给水系统模型辨识

卢晓玲，马平

（河北省发电过程仿真与优化控制工程技术研究中心（华北电力大学），河北保定 071003）

给水控制系统是超临界直流锅炉的重要控制系统之一，建立超临界机组给水系统的精确数学模型是保证给水控制质量的重要基础。鉴于超临界直流炉的复杂性，传统辨识方法已很难辨识出精度较高的模型。针对超临界机组的特点和传统模型辨识的缺点，将粒子群算法用于给水过程模型辨识，以某600MW超临界机组为例，基于电厂实际运行数据，建立了分离器出口（中间点）比焓与给水流量之间的传递函数，验证结果表明所辨识模型能够很好地反映实际运行曲线，为超临界机组给水控制系统的设计提供了前提保证；同时，粒子群辨识方法提高了模型辨识的快速性与准确性。

超临界机组；给水系统；粒子群；辨识；比焓；给水流量；传递函数

0 引言

给水控制在超临界机组控制中占有重要地位，是整个火力发电系统中的关键部分，超临界直流锅炉的给水控制与汽包锅炉不同，其控制任务是以中间点温度或焓值作为表征量，进而控制汽温和不同负荷下的给水量，给水调节品质直接关系到锅炉汽水系统能否安全、稳定运行［1］，如何建立实用有效的给水系统数学模型，在火电机组给水系统仿真与控制系统的设计研究中具有重要意义。

对超临界直流锅炉而言，汽温、汽压、给水量及蒸发量相互关联，耦合性极强，机理建模法已很难得到精确的数学模型；而现场数据的不规则性又使阶跃响应法等传统辨识方法的经验结果精度并不高［2］，建立此类复杂对象的数学模型，系统辨识法显现出了极大的优越性，本文将粒子群算法应用于模型辨识。

粒子群算法（PSO）模拟社会群体的行为，是全局优化算法，它通过构造粒子群在多维空间中寻优，粒子通过修正自身的前进方向和速度，最终找到最优区域。仿真结果表明，将粒子群算法应用于超临界机组给水系统模型辨识的方法简单易行，且辨识出的模型具有较高的精度［3］。

1 粒子群优化算法

1.1 粒子群算法原理

PSO算法受启发于鸟群觅食群体活动。鸟群寻找食物时，随机搜索某个区域里的食物，食物在此区域中的位置是唯一的，各个鸟都知道自己距离食物有多远，此信息在鸟群之间是可以共享的，同伴的位置也是每只鸟都知道的，位置的优劣取决于距离食物的远近。因此，要想尽快找到食物，鸟要调整自己的飞行方向和速度，这个过程要以每只鸟曾经经历过的最优位置Pi和鸟群发现的最优位置Pg为依据。鸟群通过共享动态信息，可以很快将食物找到［2］。

PSO算法简单易行，不需要遗传算法（GA）等其他类群体智能算法中的复杂个体和交叉变异。首先，在n维搜索区域中，将个体看成没有体积和重量的粒子，在搜索区域中以vi的速度飞行。飞行速度vi的动态调整依据个体和及群体的飞行经验。

设Xi（t）＝（xi1（t），xi2（t），…，xin（t）），为粒子i在n维搜索空间中t时刻的位置。Vi（t）＝（vi1（t），vi2（t），…，vin（t）），为粒子i在n维搜索空间中t时刻的飞行速度。Pi（t）＝（pi1，pi2，…，pin（t））为粒子i在n维搜索空间中t时刻前所经历的最好位置，叫做个体最优值［2］。

对于最小值优化问题，目的是求目标函数的最小值。设最小优化问题的目标函数为f（X），通过下面的式子确定粒子i下个时刻的最优位置：若f（xi（t+ 1））≥f（pi（t）），则Pi（t+1）＝pi（t）。若f（xi（t+ 1））≤f（pi（t）），则Pi（t+1）＝Xi（t+1）。设粒子总数为m，全局最优值为Pg（t），则

Pg（t）∈｛P0（t），P1（t），…，Ps（t）｝|f（Pg（t））＝min｛f（P0（t）），f（P1（t）），…，f（Ps（t））｝粒子根据当前的速度vij（t），个体最优位置Pij（t）和粒子群的最优位置Pgj（t）决定下一时刻的速度vij（t+1）。在决定下个时刻的速度vij（t+1）时要保留速度vij（t），还要考虑Pij（t）的影响；另外，Pgj（t）是所有粒子的目的地。基于以上信息，基本粒子群算法根据下式更新速度和位置：

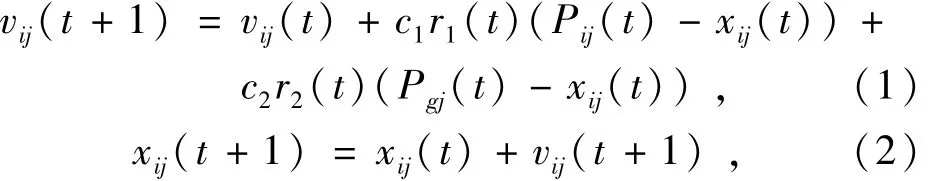
式中：i＝0，1，…，m为粒子数；j＝0，1，…，n为粒子的维数；t为粒子进化的代数；vij（t）是粒子i在j维空间中第t次的迭代速度；xij（t）是粒子i在j维空间中第t次的迭代位置；Pij（t）为粒子i在第t次迭代中j维的个体最优值；Pgj（t）第t次迭代前第j维的全局最优值；r1，r2是随机数，二者相互对立，取值范围为（0，1）；c1，c2被称作加速权重，取值范围通常为（0，2］。为防止进化过程中粒子超出搜索空间范围，限定vij在一定范围中，vij∈［-vmax，vmax］。若搜索空间在［-xmax，xmax］内，则vmax＝kxmax，0.1≤k≤1.0。粒子在迭代中，粒子在搜索空间中的位置更新原理可用图1来表示［2］。

图1 单个粒子进化过程原理图

1.2 PSO算法流程

（1）初始化，包括定义初始种群（速度-位移模型以及种群大小等），进化代数以及一些修正改进算法中可能用到的常量。

（2）评价种群。算出初始化种群中各个粒子适应度。

（3）求出当前的Pij（t）和Pgj（t）。

（4）速度和位置更新。

（5）评价种群。算出更新后的种群中各粒子适应度。

（6）比较Pij（t）和Pgj（t），择优录用。

（7）判断算法结束条件（包括精度要求和进化代数要求），满足则跳出循环，不满足则跳到流程（4）继续执行［6］。

1.3 标准粒子群法

标准粒子群算法是指带惯性权重的PSO，是基本粒子群算法的一种改进算法是在式（1）中引入一个惯性权重w，即

惯性权重w的引入是为了平衡全局搜索和局部搜索，w代表了原速度在下一次迭代中所占的比例，w大，原速度影响大，有较强的全局搜索能力；w小，原速度影响小，有较强的局部搜索能力。适当的w值在搜索速度和搜索精度方面起协调作用。一般采用惯性权重递减策略，即在算法的初期取较大的惯性权重w以对整个问题空间进行有效的搜索，算法进行后期取较小惯性权重w以利于算法的收敛。惯性权重递减公式为

式中：wmax和wmin分别为w的最大和最小值，w通常取［0.8，1.2］范围内的某值；Tmax是最大迭代次数；t是当前迭代次数［2］。

2 机组给水流量和中间点焓值特性建模

2.1 数据预处理

以某电厂600 MW超临界火电机组为研究对象，分别采集机组运行在70%额定负荷和100%额定负荷工况下的主给水流量和分离器出口温度压力运行数据，根据分离器出口温度压力数值计算出中间点焓值，由于实际运行现场存在多种干扰因素，为减小所采集数据中扰动因素对辨识模型精度的影响，对数据进行预处理。读取现场数据，经过零初值及平滑处理后的数据曲线如图2、图3所示。

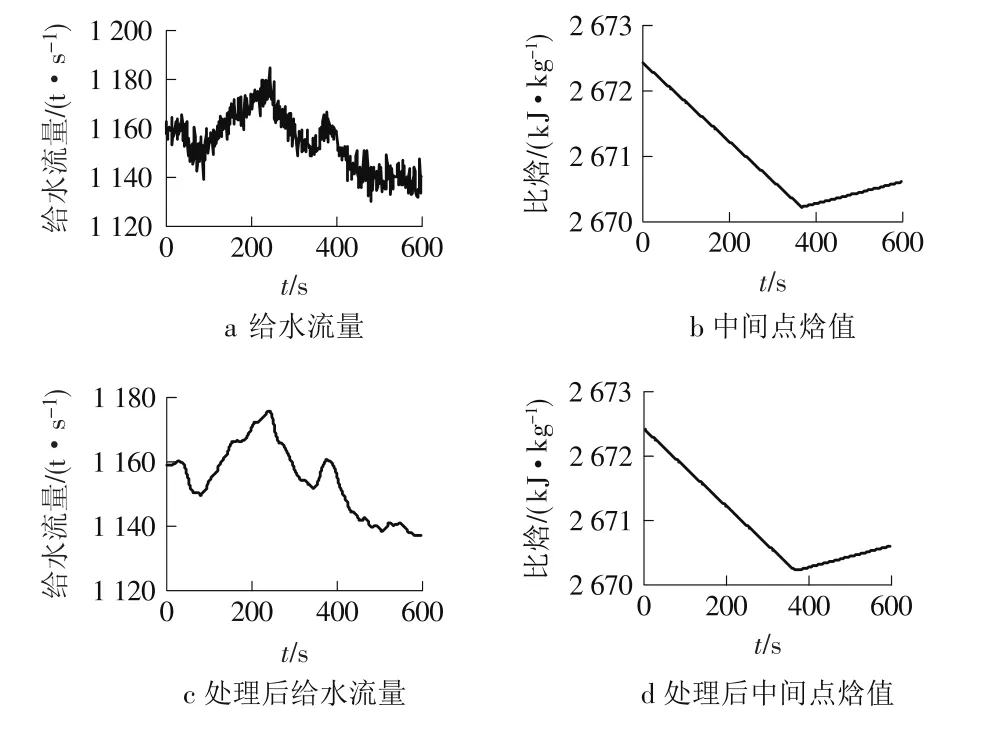
图2 70%负荷现场数据及处理后的数据曲线

2.2 模型辨识

系统辨识的过程实质上是函数拟合的过程，包括传递函数的结构和参数，面临的是结构优化和参数优化的问题，首先需要对系统有一定的了解，先给出系统模型描述函数的结构，然后辨识出函数中的参数即可［4］。超临界机组运行时，给水依次流过省煤器、水冷壁到达汽水分离器，完成加热和汽化过程到达中间点，存在惯性和迟延；超临界机组给水流量扰动下（例如给水流量阶跃增加），燃水比减小，蒸发段延后，中间点焓值下降至某一稳定水平［6］，说明超临界机组给水流量发生变化所引起分离器出口

图3 100%负荷现场数据及处理后的数据曲线

（中间点）焓值变化的过程是一个具备自平衡能力的过程。综合以上分析，选定整个被控对象的传递函数结构为

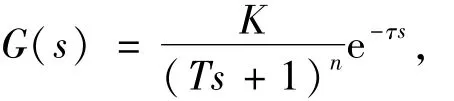
式中：K为系统增益；T为系统惯性时间常数；τ为纯迟延时间常数；n为惯性部分的阶次［7］。

辨识过程中综合考虑程序运行时间和所辨识模型的准确性，取粒子个数M＝50，进化代数s＝80，惯性权重w＝1.2，加速权重c＝［2 2］进行辨识，由于粒子群算法中含有随机操作，每次运行程序时会得到不同的运行结果，通过多次运行选择辨识结果误差最小的一组，在辨识过程中高阶参数暂定为2阶，辨识误差较大，阶数改为3阶时，取得了较为理想的辨识结果，如图4、图5所示。

图4 70%负荷辨识结果与实测数据对比曲线

辨识结果分别为

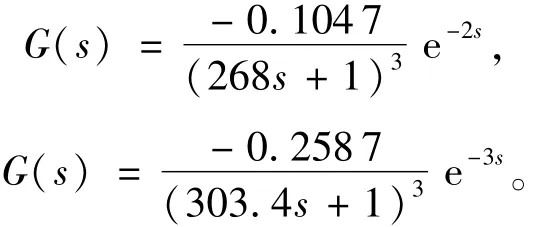
图5 100%负荷辨识结果与实测数据的对比曲线

两次辨识的误差分别为0.087 56和0.076 58，由图4、图5亦可知标准粒子群算法辨识曲线与实际曲线拟合良好，说明辨识结果具有较高的精确性。同时，不同负荷下传递函数的参数并不相同，说明超临界机组给水系统具有非线性特性，为了进一步说明该给水系统的动态特性，分别给予2种负荷下的传递函数以给水流量单位阶跃扰动，应用Simulink画出各自的单位阶跃响应曲线如图6所示。

图6 70%负荷和100%负荷下的阶跃扰动曲线

由图7可见，100%负荷下系统惯性、增益和纯迟延时间较70%负荷下增大，需要调节速度更快的控制器，不同负荷下中间点焓值对相同的给水扰动有不同的响应，说明机组在不同的负荷下有不同的动态特性（具有非线性特征），不同负荷下超临界机组需要不同的给水控制系统。

3 模型验证

为了验证模型的正确性，首先在该超临界机组的全况仿真机中，分别采集机组70%负荷和100%负荷工况下的主给水流量和分离器出口温度压力运行数据，然后分别将各自的粒子群辨识数学模型变成仿真模型连入仿真机中［8］代替原仿真模型，给予与各自模型嵌入前完全相同的仿真环境，再次抽取主给水流量和分离器出口温度压力数值，分别根据前后两次采集数据计算机组运行时分离器出口比焓，利用MATLAB画出比较结果如图7、图8所示。

由图7、图8可以看出，无论在70%负荷工况下，还是在100%负荷工况下，分离器出口比焓实际值与粒子群辨识模型输出值都十分接近，充分说明了所辨识模型的准确性。

图7 70%负荷模型验证结果

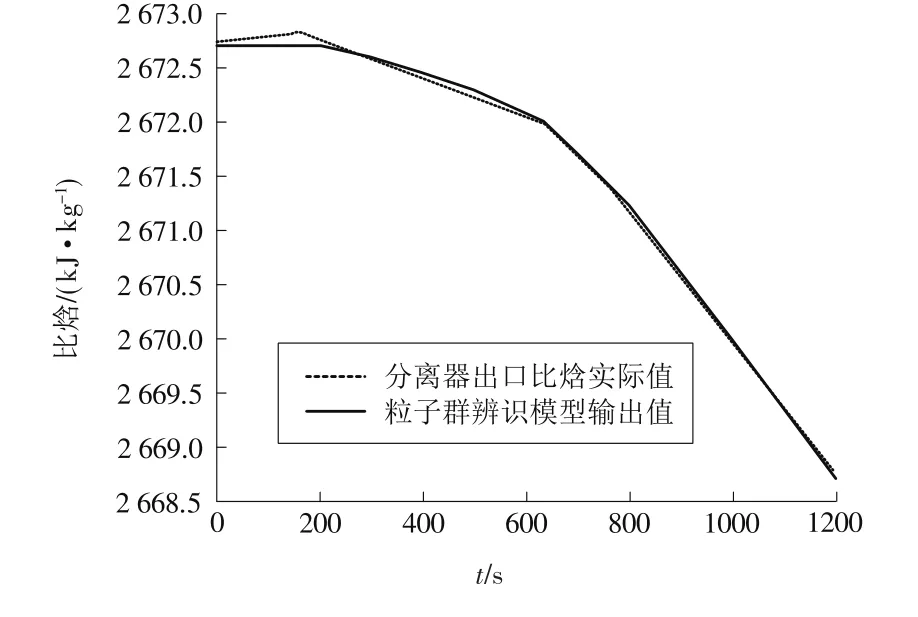
图8 100%负荷模型验证结果

4 结论

基于标准粒子群算法，建立了某600MW超临界机组给水流量与分离器出口（中间点）焓值的数学模型，结果表明，这种模型结构合理，应用实际数据所辨识出的模型包含了实际干扰因素，更接近实际应用，粒子群辨识方法快速、准确。

超临界机组在70%负荷和100%负荷时具有不同传递函数，施加相同扰动得到不同响应，验证了超临界给水对象的非线性特性，说明超临界机组给水控制系统不能固定不变。在其他负荷工况下，文中所述模型结构仍然适用，机组工况发生变化时，将机组变工况实际运行数据重新导入辨识程序即可得任意工况下的传递函数，所得结果能正确反映超临界机组给水系统的动态特性，利于超临界机组给水控制器的设计与研究。

［1］米克嵩，王波，杨建蒙.基于系统辨识的超临界600 kW机组给水控制热工对象建模与仿真［J］.应用能源技术，2011（9）：26-29.

［2］韦根源，王兵树，马磊.基于粒子群算法的1000MW火电机组模型辨识［J］.计算机仿真，2013，30（7）：400-402.

［3］张洪涛，胡红丽，徐欣航，等.基于粒子群算法的火电厂热工过程模型辨识［J］.热力发电，2010，39（5）：59-61.

［4］韩璞.智能控制理论及应用［M］.北京：中国电力出版社，2012.

［5］刘峰.超临界直流锅炉给水控制系统优化及应用［D］.河北：华北电力大学，2013.

［6］于荣生，徐二树，马进.超临界压力直流锅炉的数学模型及其仿真［J］.中国电力，1996，29（7）：20-25.

［7］何同祥，牛玉广.采用控制中间点焓值的直流锅炉给水控制系统［J］.华东电力，1999（2）：26-28.

［8］马良玉，高志远.基于神经网络的超临界机组数学模型［J］.动力工程学报，2013，33（7）：517.

（本文责编：白银雷）

U 463.5

：A

：1674-1951（2015）01-0009-04

卢晓玲（1988—），女，河北保定人，在读硕士研究生，从事火电机组建模与仿真方面的研究工作（E-mail：993927210＠qq.com）。

2014-05-30；

2014-10-06

马平（1961—），女，河北保定人，教授，从事过程控制、火电厂单元机组控制和优化、计算机原理及应用教学科研工作（E-mail：maping2067＠163.com）。