基于DOE和改进模拟退火算法的消声器优化设计

张俊红，朱传峰，毕凤荣，王 健，李忠鹏

(天津大学 内燃机燃烧学国家重点实验室，天津 300072)

在消声器优化设计中，目前国内外多以选型设计为主，加以局部改进，难以达到预期设计效果［1－3］，虽然随着计算机技术的发展，国内外采用新的理论如遗传算法等对消声器进行优化设计，取得了一些成果，但也应承认，对消声器优化设计时，一方面由于涉及参数较多，在未简化优化模型的情况下会影响消声器的优化效率，另一方面很少考虑消声器内气体流速对消声器优化结果的影响，此外优化时大部分都只考虑了某一频率的情况，较少针对排气噪声峰值，也未同时考虑排气噪声在多个峰值频率处的情况。

基于以上原因，本研究在建立消声器传递损失数值模型的基础上，针对实验测取的发动机排气噪声，提出以下优化设计方案:① 基于DOE方法辨识出对消声器性能影响较大的参数，简化消声器优化的数值模型;② 考虑消声器内气体流速对消声器性能的影响，对不同入口流速下的消声器进行结构优化设计;③ 分别以消声器在排气噪声单个峰值频率和多个峰值频率处的传递损失为对象，用改进模拟退火算法即自适应模拟退火算法(ASA)和多目标模拟退火算法(MOSA)对其进行优化。该方法能明显提高消声器优化效率，使优化设计更具有针对性，可降低排气噪声和设计成本，为以后的优化设计提供新思路。

1 排气噪声测量及结果分析

排气噪声的测量是在半消声室内进行，为了减少辐射噪声对排气噪声的影响，对发动机进行了隔声处理。根据国标GB4759－1995，排气噪声测点的位置布置在与排气口气流轴向成45°方向上距离0.5 m处，测量时传声器指向排气口，实验测试如图1所示。调整发动机转速从1000 r/min开始，以200 r/min的转速递增至额定转速2200 r/min，测量发动机外特性曲线上各个转速下的排气噪声。

图1 排气噪声测量图Fig.1 The measurement of exhaust noise

通过实验测试，得到发动机各个转速下排气噪声的频谱图，发动机排气噪声的峰值主要为各转速下的发动机发火频率及其倍频，且随着转速的升高，排气噪声的总能量也逐渐升高。当额定转速时，排气噪声的声压级达到118.40 dB。图2为在1000 Hz内发动机额定转速时的排气噪声频谱，排气噪声声压级在220 Hz、330 Hz、440 Hz处出现较为明显的峰值，且在220 Hz处声压级达到最大值118.10 dB。

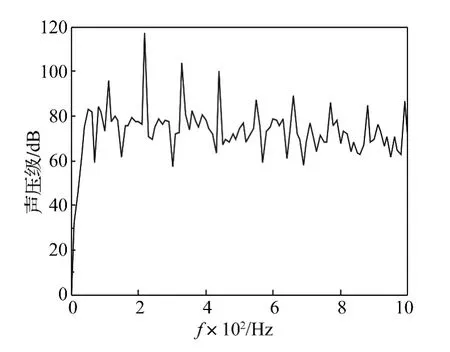
图2 发动机额定转速时排气噪声频谱图Fig.2 Engine exhaust noise spectrum at the rated speed

2 消声器模型研究

2.1 消声器数值建模

用于控制发动机排气噪声的原始消声器的轮廓图和声学节点如图3所示，由4种基本消声单元组成，分别为直管、直入口扩张管、直入口收缩管、侧入口扩张管，整个消声器的节点声压P和声学质点速度u由1～10表示。

图4为消声器的4种基本消声单元，考虑管道中气体平均流速，基于平面波理论，利用管道中截面突变处声压和声体积速度连续原理［4－7］，可得到消声器基本单元的声传递矩阵表达式。

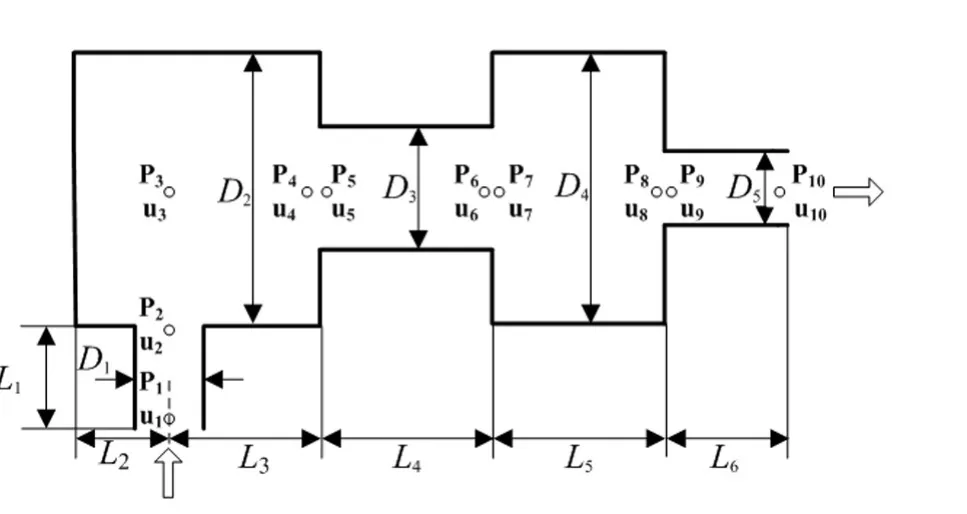
图3 消声器轮廓和声学节点Fig.3 Outline and acoustical field of the muffler

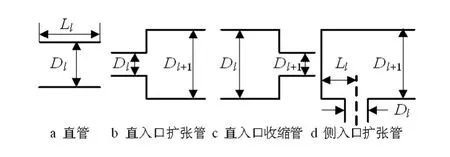
图4 消声器基本消声单元Fig.4 Basic silencing units of the muffler

(1)直管

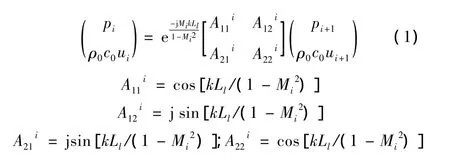
其中;i取 1、3、5、7、9。

(2)直入口扩张管

其中:i取6。

(3)直入口收缩管

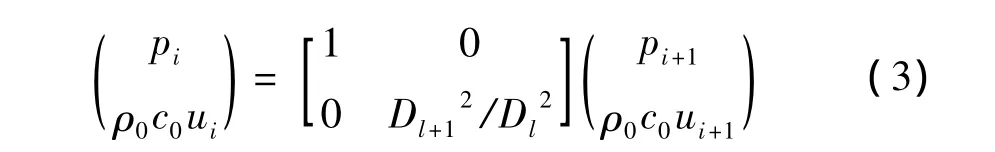
其中:i取4、8。

(4)侧入口扩张管

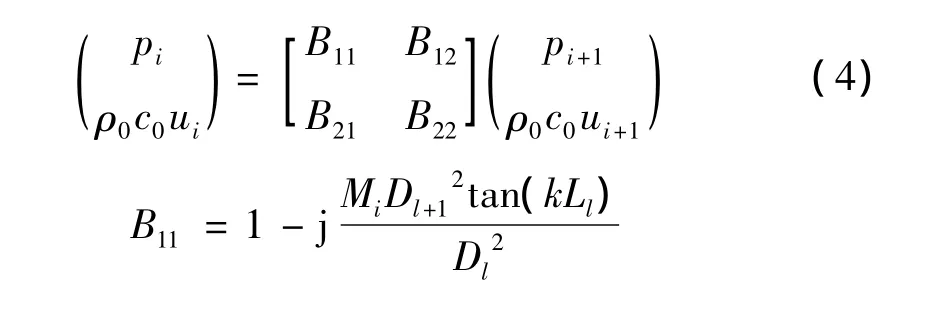
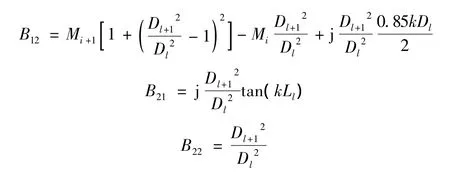
其中:i取2。

根据传递矩阵法，得到消声器的总传递矩阵为:

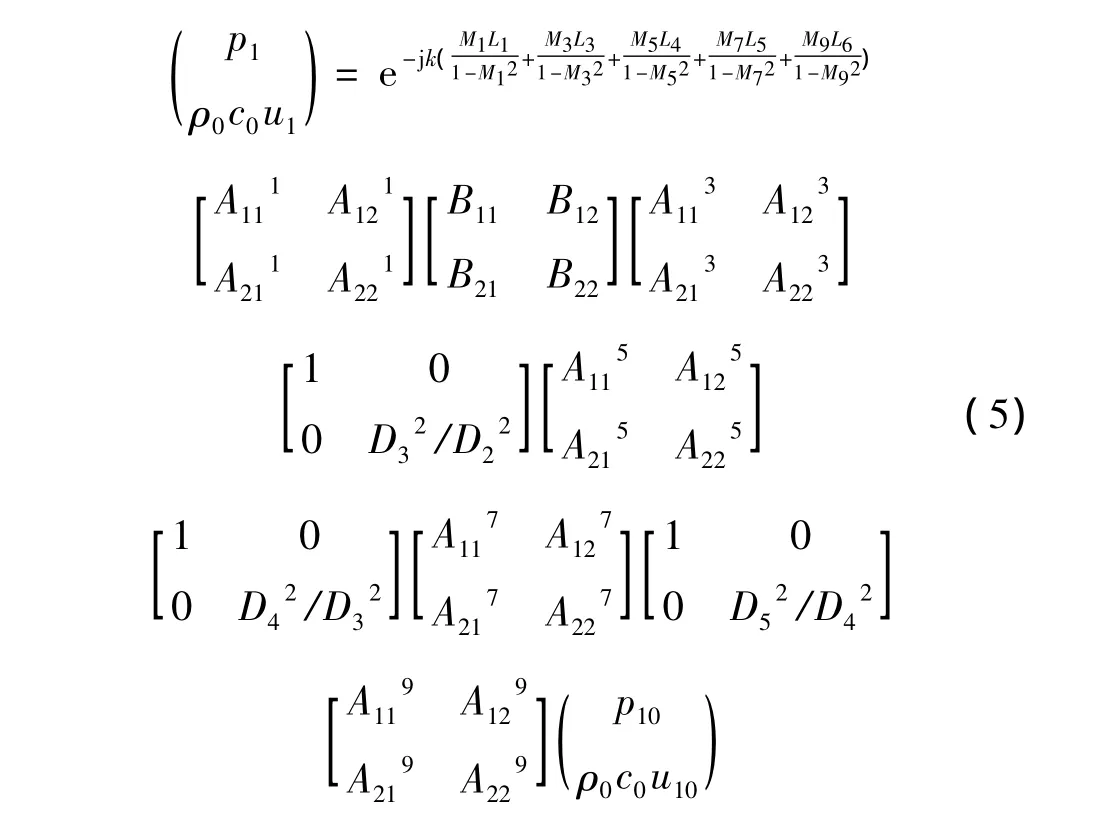
对式(5)化简，得到如下表达式:

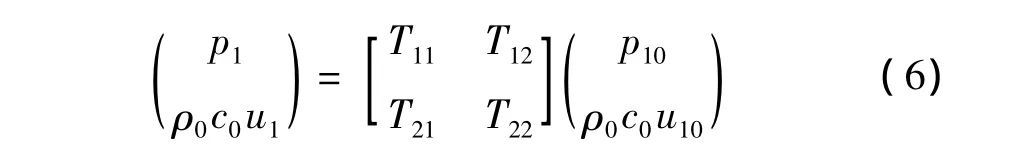
由消声器的传递损失(TL)定义，可得:

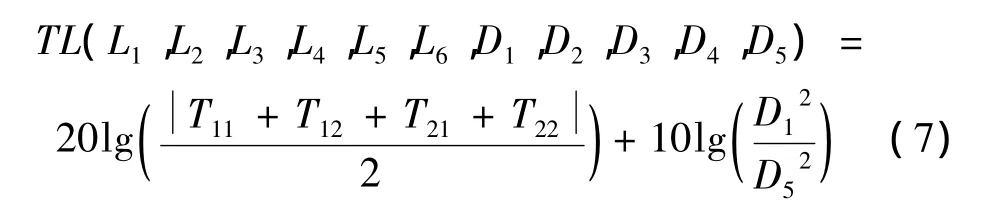
上述各式中符号在图3、4中大都有标明，未标注符号意义如下:j为虚数单位，ρ0为空气密度，c0为声速，k 为波数，M1、M2、M3、M5、M7、M9为各个声学节点处的气流平均马赫数。

2.2 模型验证

为验证消声器传递损失数值模型的准确性，分别对消声器进行有限元仿真和实验测试。用Proe建立消声器三维实体几何模型，并将模型导入Hypermesh中进行几何清理和网格划分。按照消声器声学网格质量的要求，网格单元的雅克比大于0.7，体扭曲角小于0.8，得到标准的消声器声学四面体网格模型，节点数为63641个，单元数为44068个。在声学仿真平台Virtural.lab中，对消声器入口施加单位速度激励，出口施加管口导纳条件，其它面默认为刚性壁面，进行声学性能仿真分析。图5为消声器声学有限元网格模型和330 Hz处声压云图。

图5 消声器声学有限元网格模型和330 Hz处声压云图Fig.5 Acoustical finite element mesh model of muffler and sound pressure contours at 330 Hz

基于四传声器法在半消声室内对消声器进行传递损失测量，图6为其原理图，在消声器进出口各放置两传声器，用于分解入射波和反射波。其中P1j、P2j分别表示消声器进出口的入射声压，P1r、P2r分别表示进出口端的反射声压。通过测量入射声压和反射声压可得到消声器传递损失。

图7为消声器传递损失对比图，可知在所研究频率范围内，基于数值模型得到的消声器传递损失与有限元仿真、实验值吻合较好。所建数值模型可以作为消声器传递损失的计算方法。

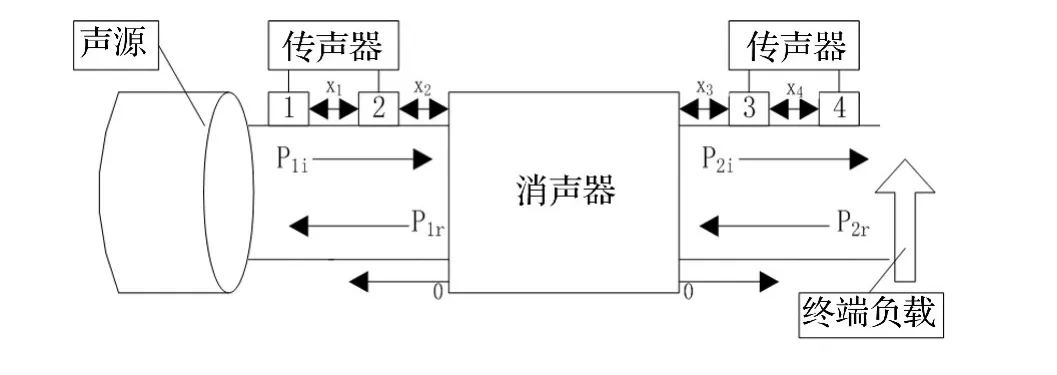
图6 消声器传递损失测量原理图Fig.6 Measurement principle of transmission loss of muffler

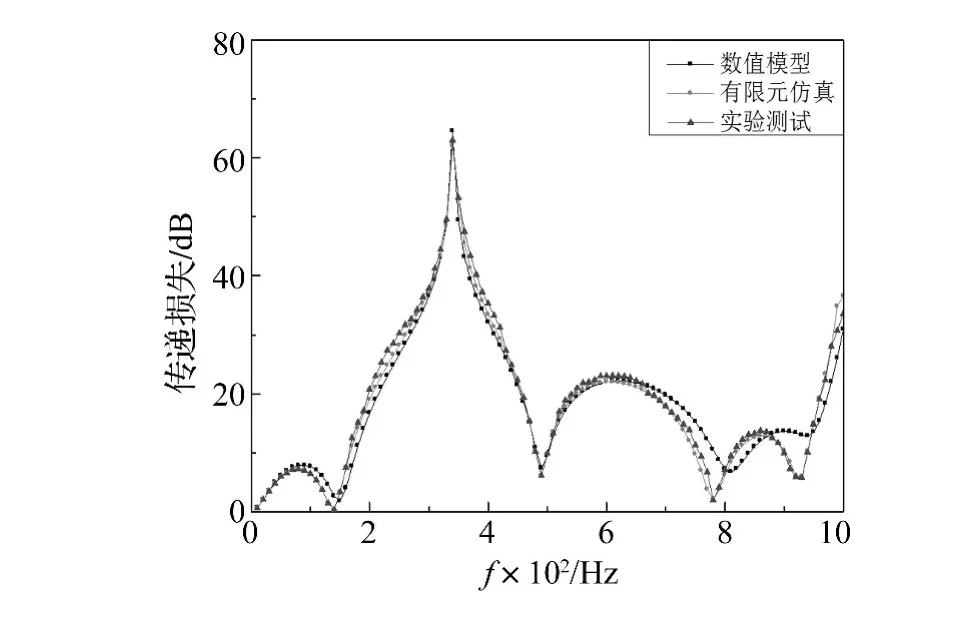
图7 消声器传递损失对比图Fig.7 Contrast figure of transmission loss of muffler

3 基于DOE的消声器参数分析

DOE是数理统计学的一个分支，由试验计划、执行试验和结果分析组成，能够辨识关键的试验因子［8－9］。在对消声器优化设计时由于涉及参数较多，为了提高优化效率，首先用DOE对消声器进行几何参数分析，辨识出关键参数。拉丁超立方设计是DOE设计中的一种，是在n维空间中，将每一坐标区间，k∈［1，n］均匀地等分为 m个区间，每个小区间记为，i∈［1，m］，随机选取 m 个点，保证一个因子的每个水平只被研究一次，即构成空间为n维，样本为m的拉丁超立方设计，和随机抽样试验和正交试验相比能够更有效的对参数进行分析［10］。

测得发动机排气管直径为0.08 m，根据实际情况选取消声器进口直径和排气管一致，并测得消声器入口处流量为0.6 m3/s。按照图8所示的拉丁超立方试验设计样本空间生成流程，考虑计算效率取200组设计变量组合进行计算，生成且输出参数设计矩阵D200×10。通过设计变量在某水平时所有随机参数组合的响应平均值对设计变量和考察指标间的关系进行二次线性回归分析［11－12］，表达式如下:

当今世界，知识经济深入发展、创新发展加快推进。在我国经济发展新常态下，知识产权制度已经成为激励创新的基本保障，知识产权已经成为发展的重要资源和竞争力的核心要素。具体而言，《知识产权基本法》的立法背景包括以下三个方面。

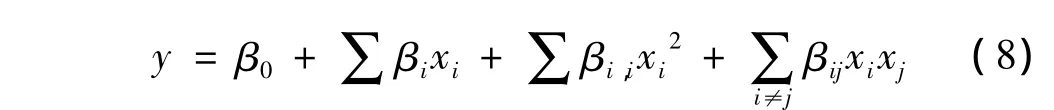
式中:y为目标参数，即消声器传递损失;xi和xj分别为设计变量，即消声器几何尺寸;β0、βi、βi，i、βij分别为对应二次线性回归模型的系数，也表明消声器几何参数对传递损失的影响程度。

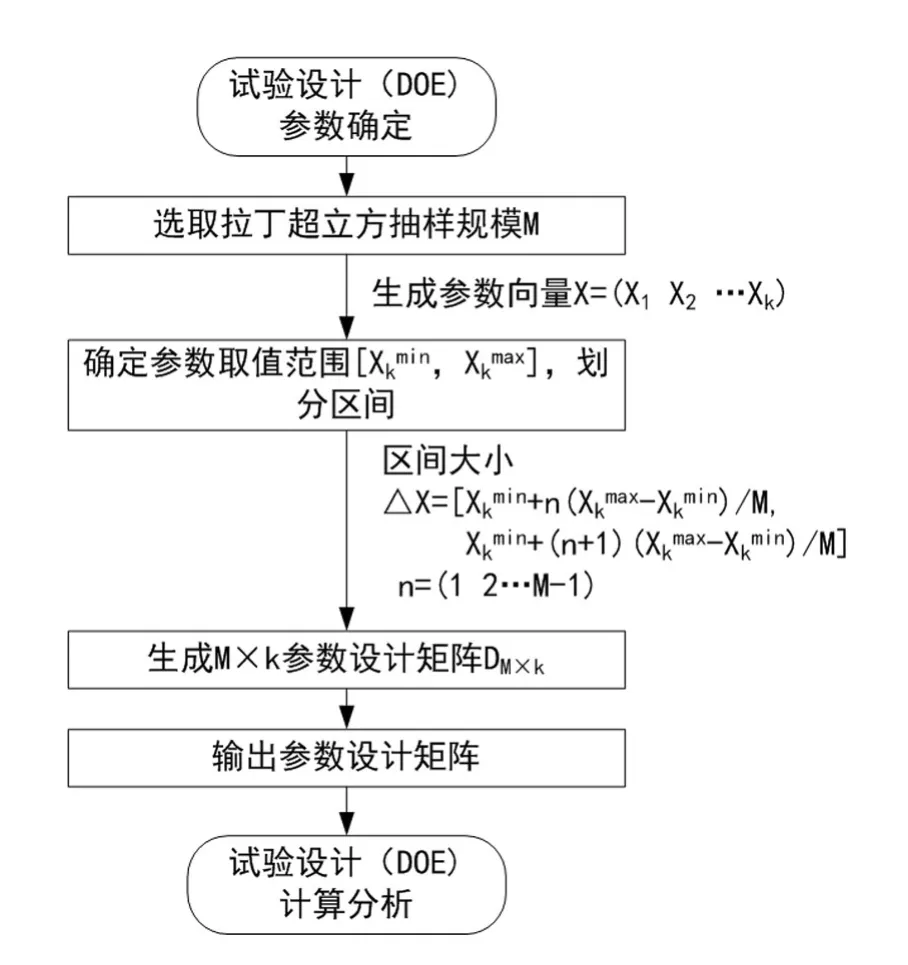
图8 拉丁超立方试验设计样本空间生成流程Fig.8 The generation process of sample space designed by Latin hypercube experimental

为公平反映设计变量对目标参数的贡献，将试验设计取值上下限分别为的设计变量xi进行归一化处理，使归一化设计变量Txi取值上下限分别为－1和1，相应转化公式为:

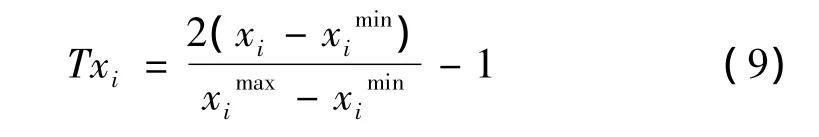
将式(9)代入式(8)可得归一化处理的二次线性回归模型，其表达式为:

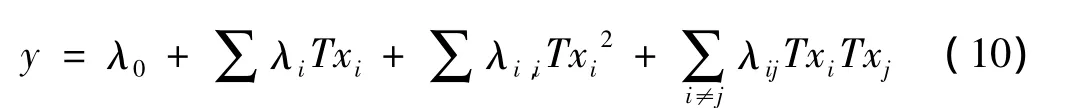
式中:λ0、λi、λi，i、λij分别为对应归一化处理后的二次线性回归模型的系数。

由系数λ转化为消声器参数对传递损失的贡献百分比 δxi为:

图9为得到的消声器参数对传递损失的贡献百分比，其中消声器几何参数 L1、L3、L6、D5对传递损失影响较小，其贡献度均小于5%，因此在对消声器进行优化设计时，可以忽略以上参数，只对关键参数L2、L4、L5、D2、D3、D4进行优化，结合发动机排气噪声频谱和消声器实际安装尺寸的限制(在长 1.0 m，宽0.3 m，高 0.3 m的范围内)，选定如下目标函数:

其中:i为频率，取排气噪声峰值频率220 Hz、330 Hz、440 Hz，其它参数设置如下:

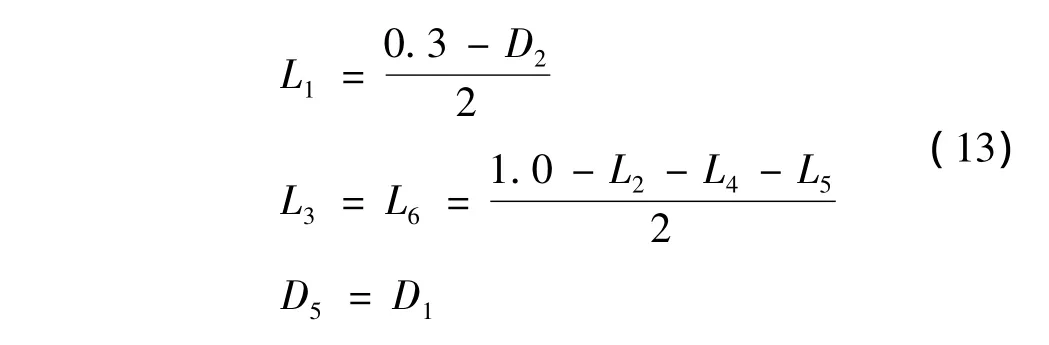
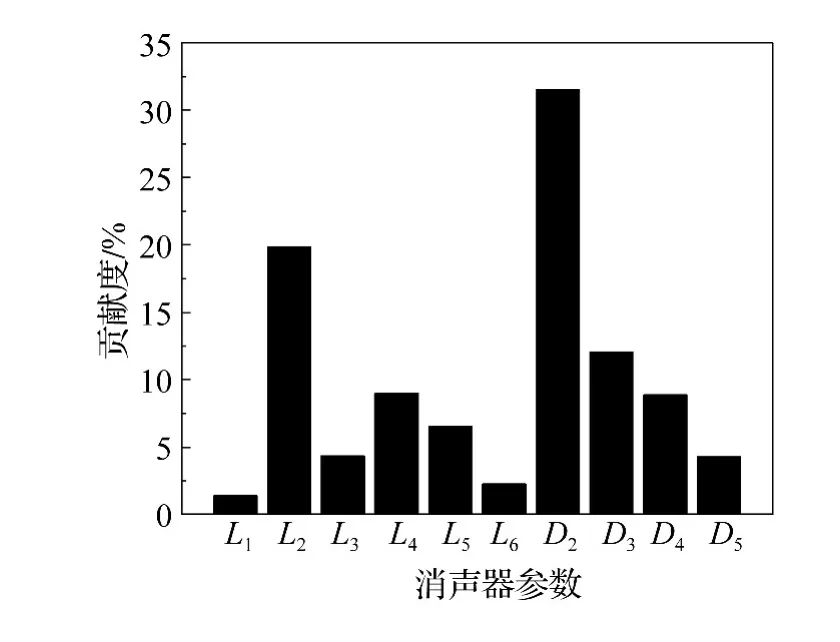
图9 消声器参数对传递损失贡献度Fig.9 Contribution percentage of muffler parameters on transmission loss

4 改进模拟退火算法在消声器优化设计中的应用

模拟退火算法(SA)具有较好的收敛性和全局求解能力［13－15］，但是由于退火过程较慢，导致优化效率不高，并且是一种单目标优化算法，不能进行多目标优化。因此通过更改温度更新函数和接收准则以提高优化效率和进行多目标优化。

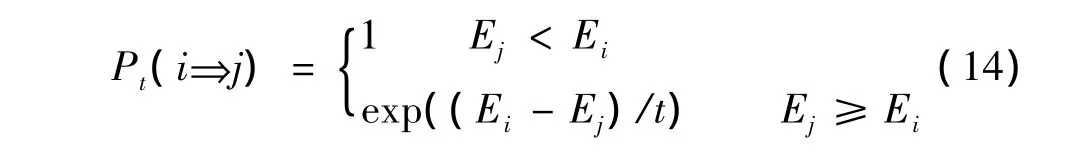
其中:E为能量函数即优化计算的目标函数。

通过将温度更新函数改为:t(k)=t0/(1+k)，形成ASA，提高了优化效率，将接收准则改为:

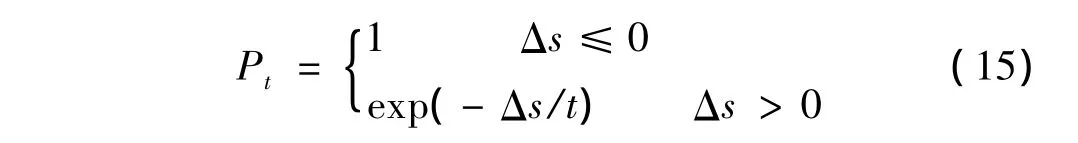
将ASA和MOSA应用到消声器的优化设计中，目标函数为式(12)，约束条件为:

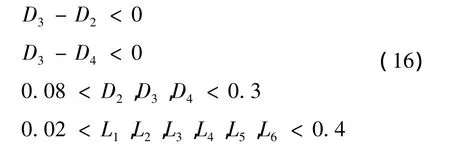
5 基于ASA和MOSA的消声器结构优化设计

5.1 不同入口流速下的消声器优化设计

消声器内气流的存在会影响消声器的性能，首先用SA和ASA对不同入口流速下的消声器进行结构优化设计，设置迭代次数都为5000。选择 OBJ220=TL(L2，L4，L5，D2，D3，D4)的最大值为目标函数，因为发动机排气噪声最大处所在频率为220 Hz，在对消声器进行优化设计时，此频率最为敏感。取消声器入口气流马赫数分别为 0、0.25、0.5，表 1 为不同入口流速下SA和ASA的消声器优化设计结果，可知:ASA和SA的优化结果相差不多，但ASA所用的优化时间明显少于SA，提高了优化的效率;随着入口流速的增大，消声器在220 Hz处的传递损失最大值逐渐减小，ASA的优化结果从90.77 dB降到82.49 dB，其中马赫数从0到0.25，下降了 2.3 dB，马赫数从 0.25 到 0.5 传递损失下降了3.98 dB，减小幅度逐渐增大;在不同入口流速下，消声器的结构优化设计结果不同，在对消声器进行优化设计前，必须测量消声器入口的流速。

表1 不同入口流速下的消声器结构优化设计Tab.1 Structure optimization design of muffler under different inlet velocities

5.2 消声器单目标优化设计

测得消声器入口流量为0.6 m3/s，分别以消声器在排气噪声峰值频率220 Hz、330 Hz、440 Hz处的传递损失最大值为目标，用ASA对消声器进行优化设计，结果如表2所示，消声器在3个频率处的传递损失最大值分别能达到87.56 dB、86.45 dB、79.81 dB。

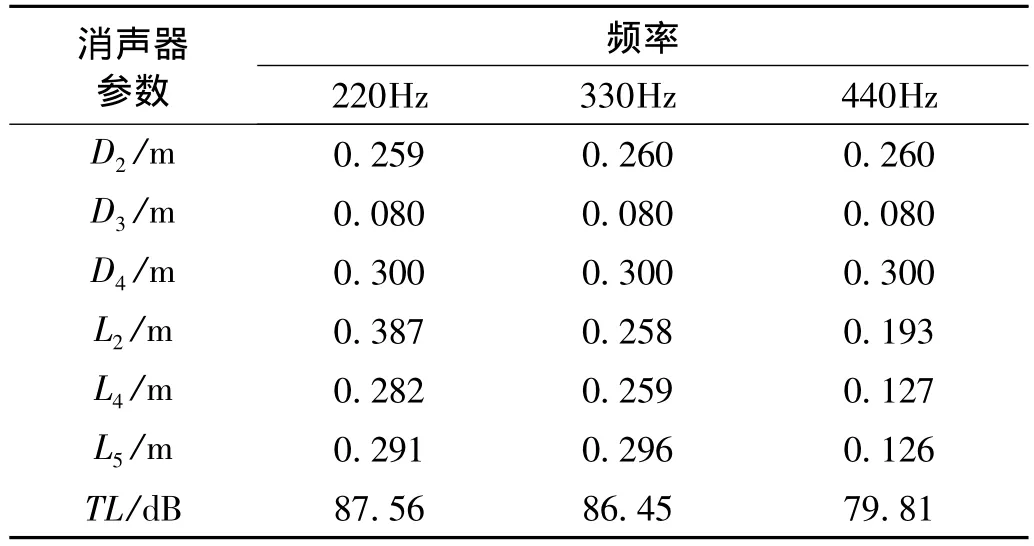
表2 单目标优化结果Tab.2 Results of single objective optimization

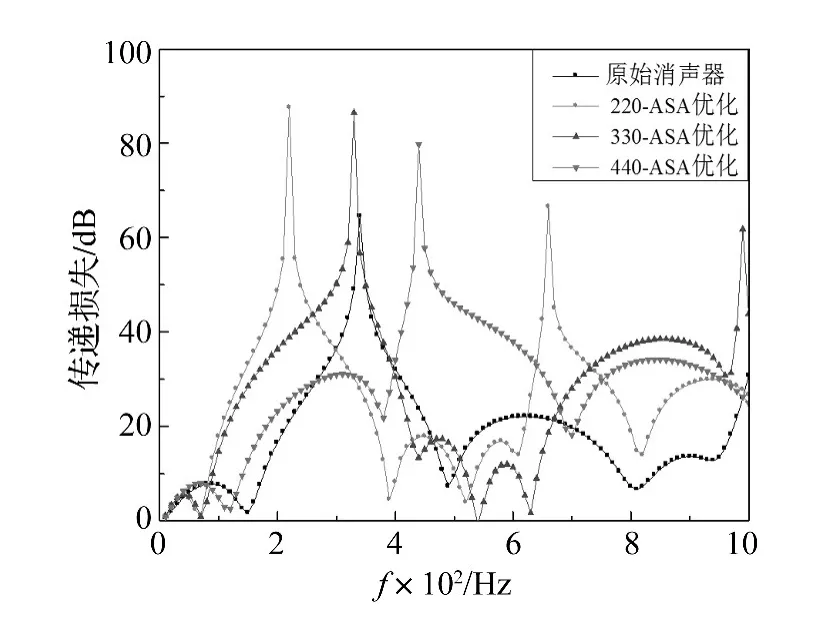
图10 单目标优化前后消声器传递损失Fig.10 Transmission loss of muffler before and after single objective optimization

图10为ASA优化得到的消声器与原始消声器的传递损失结果对比，和原始消声器相比，在大部分频率范围内消声器的传递损失都有较大的提升。原始消声器使排气噪声降低21.23 dB，而将优化后的消声器用于降低排气噪声，分别能使排气噪声降低 29.91 dB、27.47 dB、22.70 dB，分别多降低了8.68 dB、6.24 dB、1.47 dB，最大能使排气噪声降到88.49 dB，说明针对排气噪声单个峰值频率设计的消声器对控制排气噪声更有效。

5.3 消声器多目标优化设计

单目标优化时，虽然能使消声器的传递损失在单个频率处达到最大值，但无法保证消声器在其它排气噪声峰值频率处传递损失的大小，而对消声器进行多目标优化，能保证消声器在每个峰值频率处都有一定的传递损失，更有利于控制排气噪声。因此对消声器进行多目标优化。

多目标优化分为归一化和非归一化方法。归一化方法是通过设置权重系数ω将多个子目标通过加权处理得到一个总目标进行优化，但是由于权重系数的设置有很大的主观性，并且为了获得最优解，需要设置不同的权重系数组合进行多次优化，降低了优化的效率。非归一化是采用Pareto机制直接处理多个目标的优化技术，通过一次优化得到所有的Pareto最优解。

5.3.1 考虑两个频率的消声器双目标优化设计

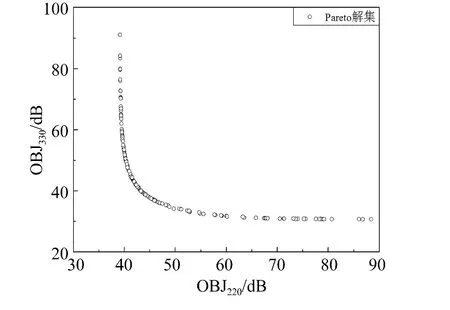
图11 Pareto最优解集Fig.11 Optimal solution set of Pareto

发动机在220 Hz、330 Hz处的排气噪声较大，以OBJ220和OBJ330同时取最大值为目标建立双目标优化模型，用MOSA对其进行优化，共得到103个解，图11为Pareto最优解集，将得到的所有解应用于控制排气噪声，选取最好的1组结果和以OBJmax=0.6×OBJ220+0.4×OBJ330为目标函数的归一化方法得到的结果进行对比，得到如表3所示的结果，非归一化方法优化后最大使排气噪声降低31.48 dB，比归一化方法多降低0.47 dB，这主要是因为归一化方法得到的结果仅仅是Pareto最优解集中的一个解，要想获得最优结果，必须不断调整权重系数ω进行优化，会严重影响消声器的优化效率。因此在对消声器进行优化设计时，采用Pareto机制的非归一化方法优于归一化方法。

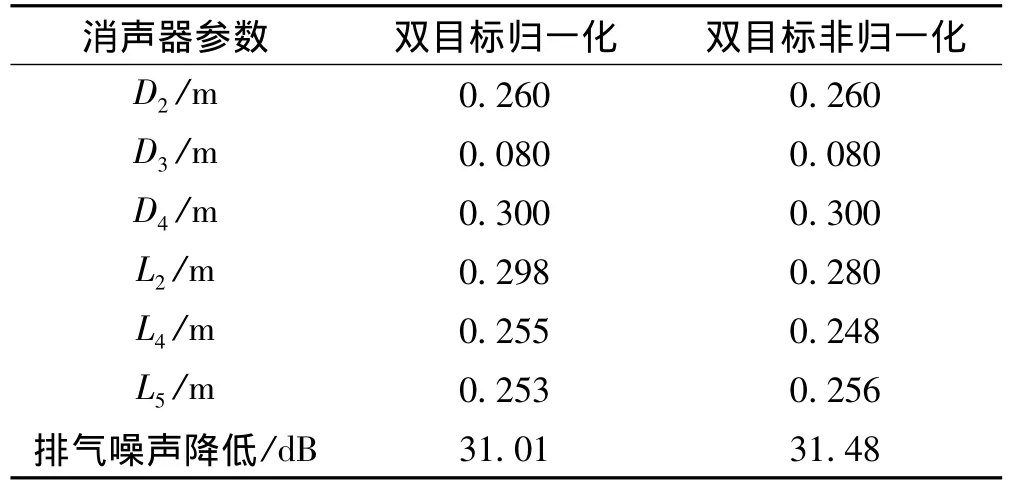
表3 双目标优化结果Tab.3 Results of double objective optimization

5.3.2 考虑三个频率的消声器三目标优化设计

以OBJ220、OBJ330和OBJ440同时取最大值为目标建立消声器三目标优化模型，用MOSA对其进行优化，共得到356个Pareto最优解，其中控制排气噪声最好的1组结果为:D2=0.260 m;D3=0.080 m;D4=0.300 m;L2=0.304 m;L4=0.123 m;L5=0.284 m，能使排气噪声降到86.67 dB，降低了31.73 dB，比单目标和双目标的最优优化结果多降低2.02 dB、0.15 dB，但是由于Pareto最优解较多，并且优化效果和双目标相差不多，考虑到优化效率，在对消声器进行优化设计时，并不是所选目标越多，效果越好，在实际工程应用中，应选择双目标进行优化设计。图12为单目标和多目标优化后得到的最优消声器的传递损失对比结果，多目标优化和单目标优化相比，消声器在排气噪声峰值频率处都有一定的传递损失。

图12 单目标和多目标优化前后消声器传递损失Fig.12 Transmission loss of muffler before and after single and multiple objective optimization

图13为用原始消声器和三目标优化得到的消声器控制排气噪声后得到的声压级对比，从图中可以看出，在大部分频率范围内排气噪声都比安装原始消声器后的排气噪声有所降低，说明优化后的消声器消声性能优于原始消声器。

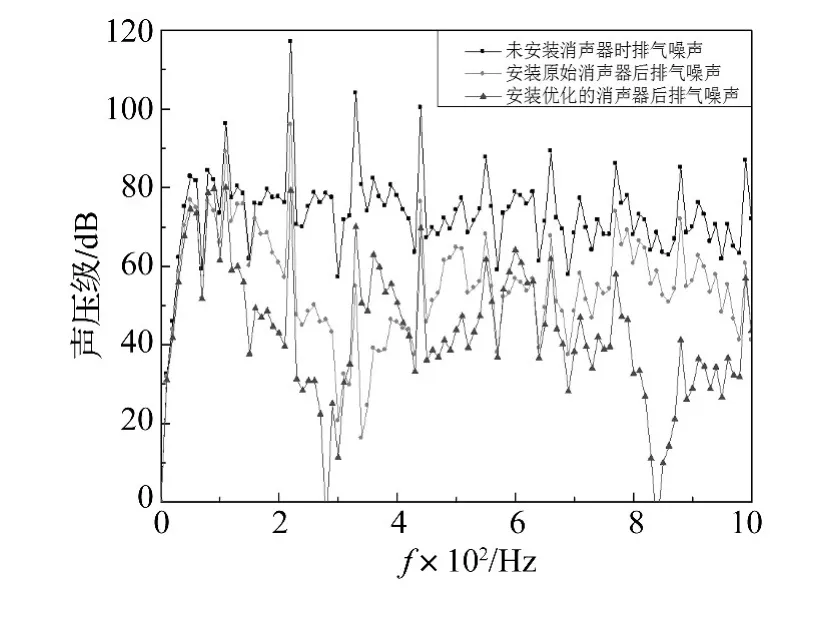
图13 优化前后排气噪声声压级Fig.13 Sound pressure level of exhaust noise before and after optimization

6 结论

(1)DOE方法能有效的识别出消声器几何参数对传递损失的贡献百分比，其中 L1、L3、L6、D5对传递损失贡献度均小于5%，在优化过程中可以忽略以上参数，简化了消声器优化的数值模型，提高了消声器的优化效率，为消声器的优化提供了新思路。

(2)由于随着消声器入口流速的变化，消声器的传递损失也相应变化，因此在对消声器进行结构优化设计时，必须测量消声器入口的流速。

(3)分别用ASA和MOSA对消声器在排气噪声峰值频率处的传递损失进行单目标和多目标优化，单目标优化可使相应峰值频率处的传递损失达到最大值，多目标优化能使全频段整体优化效果较好，优化设计后排气噪声最大降低31.73 dB，优于单目标优化结果，但是三目标的Pareto最优解较多，而最终的优化效果和双目标相差不多，考虑到工程中的实际应用，应选择双目标对消声器进行优化设计。

［1］Yeh L J，Chang Y C，Chiu M C.GA optimization on multisegments muffler under space constraints［J］.Applied Acoustics，2004，65(5):521 －543.

［2］张翠翠，吴伟蔚，陈浩.基于多目标遗传算法的消声器优化设计［J］.噪声与振动控制，2010，30(3):141－143.ZHANG Cui-cui，WU Wei-wei，CHEN Hao.Optimal design of mufflers based on muti-objective genetic algorithm［J］.Noise and Vibration Control，2010，30(3):141 －143.

［3］Goldberg D E，Holland J H.Genetic algorithms and machine learning［J］.Machine learning，1988，3(2):95 －99.

［4］Munjal M L.Plane wave analysis of side inlet/outlet chamber mufflers with mean flow［J］.Applied Acoustics，1997，52(2):165－175.

［5］Chiu M C，Chang Y C.Numerical studies on venting system with multi-chamber perforated mufflers by GA optimization［J］.Applied Acoustics，2008，69(11):1017－1037.

［6］Selamet A，Ji Z L，Radavich P M.Acoustic attenuation performance of circular expansion chambers with offset inlet/outlet［J］.Journal of Sound and Vibration，1998，213(4):619－641.

［7］胡玉梅，许响林，褚志刚.基于声传递矩阵法的汽车排气消声器设计［J］.重庆大学学报:自然科学版，2005，28(1):15－18.HU Yu-mei，XU Xiang-lin，CHU Zhi-gang.Exhaust muffler design of automotive based on acoustic transfer matrix［J］.Journal of Chongqing University:Natural Science Edition，2005，28(1):15 －18.

［8］倪计民，解难，杜倩颖，等.基于DoE的车用消声器优化设计［J］.汽车技术，2012，20(3):22－26.NI Ji-min，XIE Nan，DU Qian-ying，et al.Optimization design of vehicle based on DOE［J］.Automobile Technology，2012，20(3):22－26.

［9］叶年业，刘洁，倪计民.车用汽油机流动过程模拟及基于DoE的配气相位优化［J］.内燃机工程，2011，32(4):72－75.YE Nian-ye，LIU Jie，NI Ji-min.Flow process modelling of gasoline engine and optimization of valve timing based on DoE［J］.Chinese Internal Combustion Engine Engineering，2011，32(4):72－75.

［10］Ye K Q，Li W，Sudjianto A.Algorithmic construction of optimal symmetric Latin hypercube designs［J］.Journal of Statistical Planning and Inference，2000，90(1):145－159.

［11］王建宏，朱永红，肖绚.线性回归模型中的递推辨识及其应用［J］.振动与冲击，2012，31(15):19－25.WANG Jian-hong，ZHU Yong-hong，XIAO Xu.Application of recursive approach in parameters identification of linear regression model［J］.Journal of Viration and Shock，2012，31(15):19－25.

［12］张俊红，何文运，刘海.基于支持向量机的柴油机噪声品质客观评价参量权重分析［J］.振动与冲击，2013，32(11):112－116.ZHANG Jun-hong，He Wen-yun，LI Hai.Weight analysis of objective evaluation parameters for a diesel engine noise quality with support vector machine［J］.Journal of Viration and Shock，2013，32(11):112－116.

［13］Bouleimen K，Lecocq H.A new efficient simulated annealing algorithm for the resource-constrained project scheduling problem and its multiple mode version［J］.European Journal of Operational Research，2003，149(2):268 －281.

［14］Cakir B， Altiparmak F， Dengiz B. Multi-objective optimization of a stochastic assembly line balancing:A hybrid simulated annealing algorithm［J］.Computers＆ Industrial Engineering，2011，60(3):376－384.

［15］Damodaran P，Vélez-Gallego M C.A simulated annealing algorithm to minimize makespan of parallel batch processing machines with unequal job ready times［J］.Expert Systems with Applications，2012，39(1):1451－1458.