指数梯度半无限介质中波的传播
杨在林,黑宝平,王 耀
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
非均匀介质中波的传播研究为声波、电磁波、地震波等领域的重要课题,并逐渐成为研究热点。非均匀介质中影响波传播的变化因素较多,如弹性模量、密度、深度、波速等。其中对波数变化研究尤其重要。竖向非均匀介质中波的传播问题是研究复杂介质的基础。一维变化的非均匀介质通常体现在密度、折射率、波速、深度及波数(在一定条件下波数等效波速,两者可相互转换)等其中之一按某种函数关系在某特定方向的变化。研究竖向非均匀介质中波传播有多种方法。解析结果虽能获得理想情形,但仅当波数按某些特定形式变化及经特殊函数处理后才可获得封闭的严格解[1]。
基于Green's函数在研究均匀各向同性介质中波动问题的优越性,在对非均匀介质研究中尤其重要。在无限非均匀介质中,Hook[2]通过Green's函数法解决了常速度梯度变化的对称弹性波传播问题。Daros[3-4]研究非均匀各向异性介质中SH波基础解时,推导出一系列转化公式,用于推导线性波速变化的非均匀介质基本解研究。在此基础上采用Green's函数解决波速按指数变化的一维非均匀各向异性介质中SH波传播问题。Li等[5-7]利用 Green's函数的一重积分表达式对线性声速剖面及变化折射率剖面非均匀介质进行研究,并将此方法拓展到对声速随高度变化的大气层研究。Manolis等[8-9]运用保角映射与变量转化获得用Green's函数表示的广义Helmholtz方程基础解。对基于介质的非均匀性,广泛用于各向异性、正交同性均匀介质中的 Green's函数已发生变化,如弹性动力学Green's函数法[10]、Green's函数有限元法[11]、Green's函数谱函数法[12]等。另一种解析法通常将一维变系数波动方程转化为 Schrödinger型方程[13-16],利用路径积分解法的优越性间接求得波动解。该转化过程较复杂,尤其寻求有效代换较困难。文献[17]对脉冲点源在非均匀弹性半空间中的波动问题进行研究,将竖向、水平方向位移由介质全反射系数的积分形式表示,但结果表示较复杂,且不能对波的传播特性更深入分析。因各单元均由介质的物理性质决定,故不便于将其一般化。
本文研究点源在半无限空间内部情形,可模拟大气、海水中爆炸及地震动问题。Alekseev等[18]研究波数随深度变化时点源在自由界面情况,并认为在时域下更易解决其逆问题。对点源在半空间内部情形,研究各种特定的速度变化剖面,指数变化例外[19-20]。本文主要考虑波速以负指数次幂变化的竖向非均匀介质中波的传播问题,在分离变量基础上经Hankel函数获得在给定边界下速度势函数。波在非均匀介质传播会产生阴影区域,其大小与距点源距离及波动频率相关。
1 模型建立及边界条件
本文研究半无限非均匀空间中二维波传播问题。介质参数由波速c(z)(波数k(z)=ω/c(z))变化而定。平面x=a为全反射表面,仅研究z>a半空间在深度h处有点源P,到z轴的距离记为r,以此为边界,将半空间分为Ⅰ(a<z<b)、Ⅱ(z>b)两区域,见图 1。其中φ1,φ2分别为两区域速度势函数,在区域Ⅱ中,点源附近的势能为φs=(1/r)eikr。

图1 半无限非均匀空间中的点源PFig.1 Point source P in semi-infinite inhomogeneous space
问题的边界条件为:① 在自由表面z=a处,声压全部消失,即φ1=0;② 对区域Ⅱ(z>b),声波φ2须由点源P向外传播的发散波;③ 在z=b,r≠0处,声速分量连续,即φ1=φ2;④ 在z=b,r=0处,速度垂直分量非连续,即∂φ1/∂z- ∂φ2/∂z=-D,其中 D 为测量声波强度常数,与r方向速度势有关。
2 控制方程及解答
基于时间简谐波的线性波动方程为

声压或介质密度为

式中:c0为波速常数;ρ0为介质密度。
设Laplace变量s=υ+iω,则有 Laplace变换及逆变换[21]为
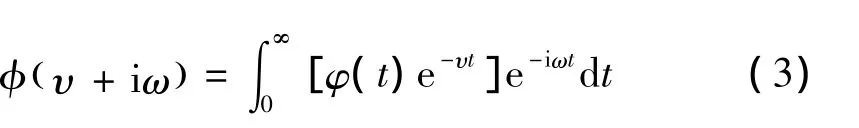

将式(4)代入式(1)去除时间因子,得相应的Helmholtz方程为

定义(υ +iω)/c0=i k,得约化 Helmholtz方程为

式中:k=(ω-iυ)/c0;(x,y,z)为平面笛卡尔坐标系。式(1)的解可表述为

式(6)可表示在特定深度下线性波传播的控制方程。全部波动势能为

式中:φ可以为压力、位移或速度势,可据边界条件的适用性选择变量。本文设其为速度势,若设υ=0,则波数k可表示为k=ω/c0,与简谐波相同。
式(8)为相对于自由表面z=a在z=b处的势能。波数k(z)与水深a+b=h(x,y)与波角频率ω关系为ω2=gk tan(kh) (9)式中:g为重力加速度。
用分离变量法解决速度势问题。式(6)在柱坐标系(r,θ,z)下表示,不考虑θ对方程的影响,设φ=R(r)Z(z),将波动方程转化为

式中:λ为在r方向的传播常数。
因速度分量在r=0、r=∞处均须为有限值故式(8)的解为

式中:J0(·)为零阶第一类Bessel函数。
设声速在z方向以负指数形式变化,则可表示为

式中:c0=2π/ω为在均匀介质中的波速;m为任意常数。
将式(13)代入式(11),可表示为


由式(1)得

则有

将式(17)代入式(3)、(4)整理得

由此确定A,C,可表示为含D的表达式,即

点源在z平面内的速度势正比于

具有任意速度势剖面c(z)的竖向非均匀介质中,速度势函数 φ 可表示为 Sommerfeld-type 积分[7,22],即

又有

式中:Hankel函数可由积分获得,即

若使式(26)收敛,H(·)可取 ζ=ξ+iη平面内W1,W2两积分路径或J(·)取W0为积分路径,见图2。
将式(25)、(26)代入式(12)可得J0(r)。从而由式(24)表示获得φ1,φ2积分表达式。
对波速设定具有一般性,令式(13)中m=0,则可退化到均匀介质中波速按常数c0恒定不变的波传播问题。此时,对应的速度势函数(24)转化为


图2 Hankel函数积分路径Fig.2 Integrating path of Hankel function
3 结论
(1)本文研究波速以负指数次幂变化的竖向非均匀介质中波传播问题。通过对半无限非均匀空间中波动方程推导、求解,获得速度势函数的积分表达式,且可退化到均匀介质,具有普遍适用性。
(2)在该非均匀介质中,由于波连续折射可会产生阴影区域,其大小可与到点源的距离及波动频率有关。该结果可为深入研究大气层中声波、地震波传播机理提供参考。
[1]БреховскихЛ М. Волны В СпоистыхСредах.ИЗД АКАЛ[M].1 - еизд.1957;2 - еизд.1974:121 -123.
[2]Hook J F.Green's functions for axially symmetric elastic waves in unbounded inhomogeneous media having constant velocity gradients [J].Journal of Applied Mechanics,ASME,1962,29(2):293-298.
[3]Daros C H.A fundamental solution for SH-waves in a class of inhomogeneous anisotropic media[J].International Journal of Engineering Science,2008,46(8):809 -817.
[4]Daros C H.Green's function for SH-waves in inhomogeneous anisotropic elastic solid with power-function velocity variation[J].Wave Motion,2013,50(2):101-110.
[5]Li Y L,Liu C H,Franke S J.Three-dimensional Green's function for wave propagation in a linearly inhomogeneous medium-the exact analytic solution[J].The Journal of the Acoustical Society of America,1990,87(6):2285-2291.
[6]Li Y L.Exact analytic expressions of Green's functions for wave propagation in certain types of range-dependent inhomogeneous media[J].Journal of the Acoustical Society of America,1994,96(1):484-490.
[7]Li Y L,Whitea M J,Taib J F.An improved approximation for wave propagation above an impedance ground in a medium with a linear sound-speed profile[J].Journal of the Acoustical Society of America,1997,102(2):1231 -1234.
[8]Manolis G D,Shaw R P.Fundamental solutions for variable density two-dimensional elastodynamic problems[J].Engineering Analysis with Boundary Elements, 2000,24(10):739-750.
[9]Shaw R P,Manolis G D.A generalized Helmholtz equation fundamental solution using a conformal mapping and dependent variable transformation[J].Engineering Analysis with Boundary Elements,2000,24(2):177 -188.
[10]Vavrycuk V. Acoustic and elastodynamic 3D Green's functions for isotropic media with a weak velocity gradient[J].Wave Motion,2000,31(3):223-236.
[11]Onyejekwe O O.Green element method for 2D Helmholtz and convection diffusion problems with variable velocity coefficients[J].Numerical Methods for Partial Differential Equations,2005,21(2):229 -241.
[12]Calveta M,Margerin L.Velocity and attenuation of scalar and elastic waves in random media:a spectral function approach[J].Journal of the Acoustical Society of America,2012,131(3):1843-1862.
[13]Razavy M. Determination of the wave velocity in an inhomogeneous medium from the reflection coefficient[J].Journal of the Acoustical Society of America,1975,58(5):956-963.
[14]Zaman F D,Masood K.Shear velocity inversion procedure for love waves[J].Journal of Technical Physics,2003,44(3):295-301.
[15]Abraham P B,Moses H E.Exact solutions of the onedimensional acoustic wave equations for several new velocity profiles:Transmission and reflection coefficients[J].Journal of the Acoustical Society of America,1982,71(6):1391-1399.
[16]Li W,Liu S B,Yang W.A new approach of solving Green's function for wave propagation in an inhomogeneous absorbing medium[J].Chinese Physics B,2010,19(3):1-3.
[17]Acharya H K.Field due to point source in an inhomogeneous elastic medium [J].Journal of the Acoustical Society of America,1971,50(1B):172-175.
[18]Alekseev A S,Avdeev A V,Fatianov A G,et al.Wave processes in vertically-inhomogeneous media:a new strategy for a velocity inversion[J].Inverse Problems,1993,9(3):367-390.
[19]Pekeris C L.Theory ofpropagation of sound in a half-space of variable sound velocity under conditions of formation of a shadow zone[J].Journal of the Acoustical Society of America,1946,18(2):295-315.
[20]Potter D S,Murphy S R.Solution of the wave equation in a medium with a particular velocity variation[J].Journal of the Acoustical Society of America,1962,34(7):963 -966.
[21]Liu G,Jayathilake P G,Khoo B C,etal.Conformalmapping for the Helmholtz equation:Acoustic wave scattering by a two dimensional inclusion with irregular shape in an ideal fluid[J].Journal of the Acoustical Society of America,2012,131(2):1055-1065.
[22]Yamada R.On the radio wave propagation in a stratified atmosphere[J].Journal of the Physical society of Japan,1995,10(1):71-77.

