LMD与非凸罚最小化Lq正则子压缩传感的轴承振动信号重建
李庆,宋万清
(上海工程技术大学 电子电气工程学院,上海,201620)
目前机械系统的运行状态监测与预测技术均建立在采集高质量的振动信号的基础上,然而,振动信号的采集必须满足 Nyquist采样定理,数据采集量一般较大,且数据存储、传输速度等往往受到采集硬件的限制,因此,机械振动信号的压缩与重构技术显得越来越重要。传统的数据压缩处理技术包括基于信号工程特征的特征值提取压缩法、基于多分辨分析的小波压缩法(阈值压缩法以及信号多尺度边沿回复压缩法)、数据压缩稀化法(分段判别和模式分类、分段压缩)等[1-4],这些方法虽降低了存储与传输负担,但仍要求采集系统具有很高的采样频率,依然存在数据压缩计算复杂、数据压缩有限、内存浪费和适用范围低等问题[5-6]。Candes等[7-9]提出压缩传感(compressive sensing,CS)理论,指出利用随机测量矩阵把稀疏可压缩的高维信号投影到低维空间中,通过求解一定的线性或非线性解码模型,能以较高的概率重建原始信号。压缩传感理论将采样与压缩合并进行,克服了Nyquist采样定理的限制,避免对原始信号直接采样,降低了对数模转换器的带宽要求,有效降低了传感器和抽样系统的复杂性。然而,压缩传感理论是把采样的复杂性转移到重构算法计算的复杂性中,且信号的稀疏度一般与信号的重构精度和计算复杂度相关;机械振动信号不同于一般的模拟信号,属于一种快速、非线性、非平稳的突变信号[10],信号稀疏性差,导致重构效率低。因此,如何降低机械振动信号重构的复杂度及提高重构效率成为这一理论研究的关键技术。Smith[11]提出一种新的时频分析方法——局部均值分解(local mean decomposition,LMD)算法。该方法可将多分量非线性信号分解为若干个乘积函数 PF的线性组合,每个PF分量通过1个包络信号和1个纯调频信号相乘得到,属于单分量的调幅调频信号。对于重构精度与重构速度,Zhang等[12]证明非凸罚最小化Lq正则子具有无偏性、稀疏性以及Oracle性等优良特性,比经典最小化 L0正则子更易求解,与最小化 L1正则子相比具有更好的稀疏性与稳健性,重构精度和速度要优于一般最优化算法。因此,结合以上2种算法思想,本文作者提出一种利用 LMD方法与非凸罚最小化Lq正则子压缩传感相结合的振动信号重构方法,利用LMD把振动信号分解为若干个平稳的PF分量,然后对每个 PF分量进行非凸罚最小化 Lq正则子 CS处理,重构得到原始振动信号。该方法充分利用 LMD算法与非凸罚最小化Lq正则子算法的优点,与直接采用 CS压缩轴承故障振动信号相比,不但信号重构精度得到提高,且计算复杂度降低,可在线应用。
1 局部均值分解(LMD)
局部均值分解(LMD)与经验模态分解(empirical mode decomposition, EMD)类似,是一种新的自适应时频分析方法。相对于EMD法,用滑动平均代替3次样条插值,LMD法在抑制端点效应、减少迭代次数和保留信号信息完整性等方面优于EMD法[12]。给定任意非平稳信号x(t),其分解步骤如下。
1) 确定信号x(t)所有局部极值ni,求相邻2个极值间的平均值mi=(ni+ni+1)/2,将所有的平均值点mi用折线连接,进行滑动平均平滑处理,得局部均值函数m11(t)。由局部极值 ni计算包络估计值 ai=|ni-ni+1|/2,将所有包络估计值ai采用滑动平均平滑处理,得包络估计函数a11(t)。
2) 从信号x(t)中分离出m11(t),得剩余信号h11(t),对h11(t)进行解调,有:
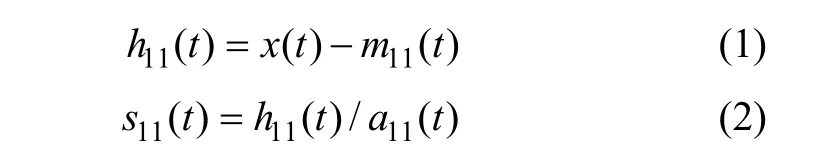
若 s11(t)为纯调频信号,则其对应包络估计函数a12(t)=1,否则,s11(t)作为原始信号重复以上迭代过程,即-1≤s1n≤1,则

3) 将迭代过程得到的包络估计函数相乘得到一瞬时幅值函数,即PF分量的包络信号
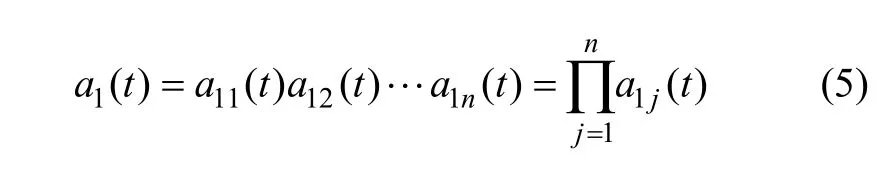
将包络信号a1(t)和纯调频信号s1n(t)相乘得到原始信号x(t)的第1个PF分量:
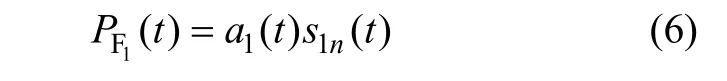
第1个分量1F()P t的瞬时幅值就是包络信号a1(t),而瞬时频率f1(t)可以通过纯调频信号s1n(t)求出,其包含信号x(t)中的最高频率成分,有

4) 从信号 x(t)中分离出1F()P t,得到新的信号u1(t)。将该信号作为新原始信号重复上述步骤K次,直到uk(t)的极值点小于或等于1为止。信号x(t)可分解为K个PF分量和残余项uk(t)之和,即
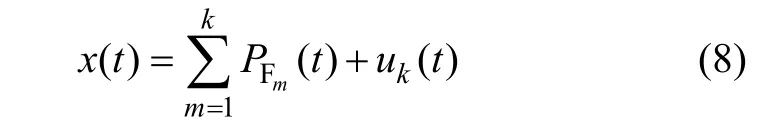
因此,LMD分解是一个逐步去除信号高频成分的过程,并没有造成原始信号的信息丢失,而信号完整的时频分布体现在所有 PF分量的瞬时幅值和瞬时频率中。
2 非凸罚最小化Lq正则子重构算法
在压缩传感中,信号的采集与压缩合并进行,信号经过非自适应性投影和求解最优化方法可高概率重构原始信号,降低了传感器的采集量与计算时间,适合对机械振动信号的长期运行的实时在线采集。压缩传感理论主要包括信号稀疏变换、测量矩阵设计和信号重构算法3部分。
2.1 信号稀疏变换与测量矩阵设计
信号稀疏变换的目的是使信号在特定正交变换基下的表示系数的绝对大部分为 0,得到含有信号绝大部分信息的系数[13]。对于给定N维信号f在标准正交基下的线性组合表示为式中,Ψi为列向量,Ψ为1个N×N维的矩阵)。若信号 f中非零元素的个数为K(KN<<),则f是K稀疏的。稀疏基有离散小波变换基(DWT)、离散余弦变换基(DCT)、快速傅里叶变换基(FFT)和Gabor基、Currelet基等[14],根据信号不同变换域下稀疏性不同,不同稀疏性影响 CS重构精度,因此,对上述LMD分解得到的各PF分量,高频分量采用离散小波变换基稀疏表示,低频与残余分量采用FFT变换基稀疏表示。
选取特定的测量矩阵Φ(M×N维矩阵)与测量次数M(MN<<),通过线性测量的方法得到信号f的测量值[15]为
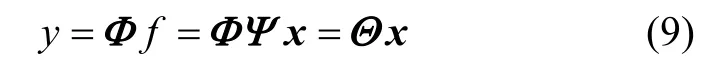
式中:Θ为传感矩阵;y为f的测量值;x为稀疏向量,其为一维矩阵。
由于KMN<<≤,方程yf=Φ的逆问题是求解欠定方程,Candes等[16]指出在保证算法收敛的情况下,K个非零元素能够有M个测量值准确的恢复,测量矩阵Φ必须满足约束等距条件时(restricted isometry property,RIP)[17],稀疏信号的重构精度才较高。常用的测量矩阵有高斯随机矩阵、局部傅里叶矩阵、局部哈达玛矩阵和二值随机矩阵等。
2.2 信号非凸罚最小化Lq正则子重构模型
由于方程y=xΘ属于高度欠定的方程,存在无数组解,但向量x是K稀疏的,从M个测量向量中可重建x。通过寻找y中满足M个测量向量的最稀疏信号,即信号x是l0最小化问题的解为
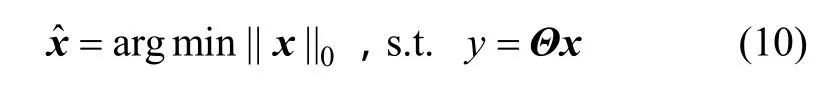
最小化l0问题是一个N-P Hard问题,Donoho指出当Θ满足RIP条件时[8,14,17],可转化为最小化模型l1:
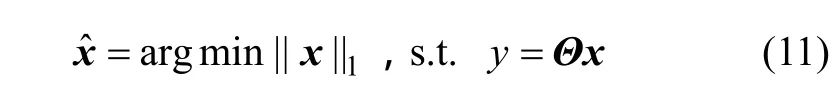
来求解,最终得到f的逼近信号 ˆ ˆ f=Ψx。
对以上最小化模型进行改进,本文提出非凸罚最小化Lq正则子(0<q≤1)方法:
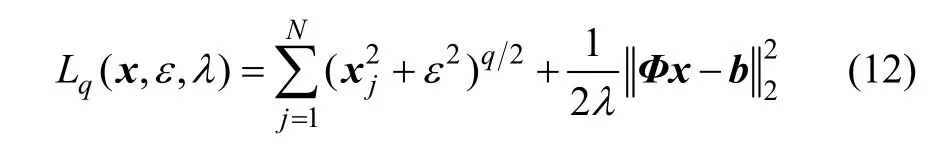
其中:ε ( ε > 0 )为平滑参数;λ ( λ > 0 )为惩罚参数;Φ为测量矩阵;b为观测向量。算法步骤[18]如下:
1) 输入:测量矩阵Φ,观测向量(信号) b。
输出:恢复向量(信号) x。
2) 选择适当的惩罚参数 λ ( λ > 0 ), q (0 < q≤1);
3) 初始化迭代向量(信号) x(0),使其满足Φx(0)=b,且ε=1;
4) 开始迭代k=0;
5) 通过x(k)解决线性问题:
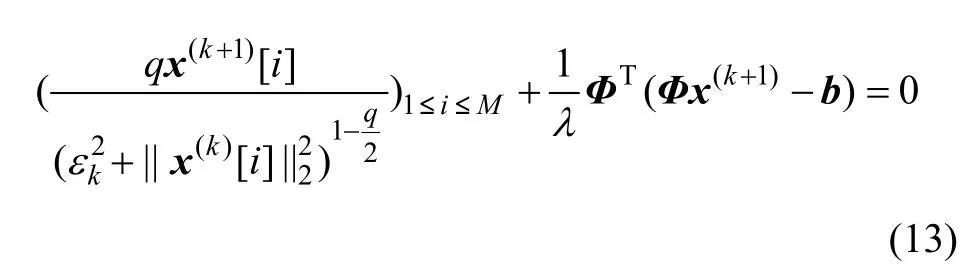
或
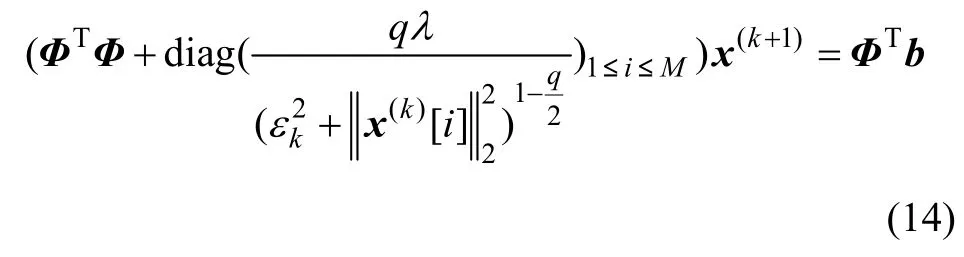
6) 当 x(k)满足要求的重构精度时,将其作为输出幅值给x,同时结束算法,否则执行下一步。
8) 令k=k+1,并返回到第4步继续执行。
2.3 模型求解与仿真
对于参数q,随机选择q属于{0.1,0.5,0.7,1.0}来重构稀疏空间向量。首先,由 MATLAB随机生成64×256的测量矩阵Φ,原始向量x0的个数n=256,含有t个非零窄脉冲原始信号,非零向量的位置均匀随机分布,t可取{8,10,12,…,32},λ设置为10-6,λ=10-6足够小使得满足 Φ x =Φx0,算法迭代1 000次,若误差满足,则算法停止(式中,xr为重建向量)。
图1(a)所示为在不同q时的重建成功率的变化图。从图1(a)可以看出:当q为0.1和0.5时,比q=0.7和1.0时的效果好;另外,当q为0.5时比q为0.1时的重构精度高;q的取值越小,最小化函数的非凸性越强,重构越困难。经研究发现:若减少平滑参数ε的变化率,则q为0.1时的重构效果更好,但是运行时间大大增加。

图1 稀疏向量重建结果比较Fig. 1 Comparison results of sparse vector reconstruction
下面仿真验证非凸罚最小化 Lq正则子重构算法与其他重构算法的效果比较,选择 L1-magic算法[19-20],加权 L1算法[21],同伦算子法[22]与 Lq-FL算法[23]。其中L1-magic算法与加权L1算法均是解决限制最小化L1算法,表达式为

同伦算子法是一种解决非限制最小化L1算法,表达式为
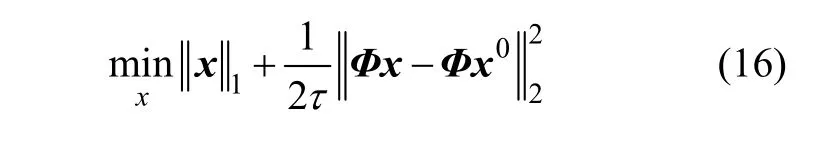
Lq-FL算法表达式为
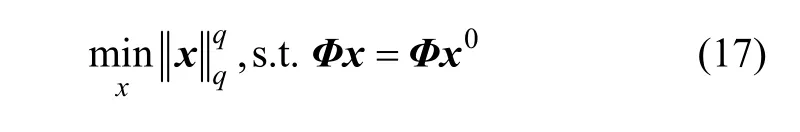
仿真验证:由MATLAB随机生成50×250测量矩阵,矩阵中每个元素满足 N(0,1/50)高斯分布;原始向量x0仍为n=256,含有t个非零窄脉冲原始信号,非零向量的位置均匀随机分布,令t取{5,7,9,25},取λ=10-6,q=0.5,同伦算子法中取τ=10-6,使每个算法迭代1 000次,若误差满足,则算法停止。重构结果比较如图1(b)所示。
从图1(b)可以看出:随着稀疏度增大,各重构算法的重构误差增大,重构成功率降低,但非凸罚最小化 Lq正则子(q=0.5)重构算法的重构效果优于其他算法的效果。
3 滚动轴承振动信号重建与分析
当轴承内圈或外圈表面发生故障时,在旋转过程中由于周期性脉冲力作用,振动加速度信号往往产生峰值较高且尖锐的高频振动信号。
图2所示为本试验所截取的某段采样点为1 024的6205-2RS型内圈有点蚀故障的深沟球轴承的振动信号时域波形。对该振动信号进行LMD分解,得到频率由高到低的各个PF分量和残余信号,分解结果如图3所示。
为了使不同频段的 PF分量达到压缩传感的最稀疏表示,高频1FP 和2FP 分量采用小波变换,低频与残余分量采用快速傅里叶变换基(FFT)稀疏表示。测量矩阵选择随机高斯矩阵,利用非凸罚最小化 Lq正则子(q=0.5)算法重构原始振动信号,对于恢复后的信号失真程度,通过如下均方根来测量信号重构相对误差ε:
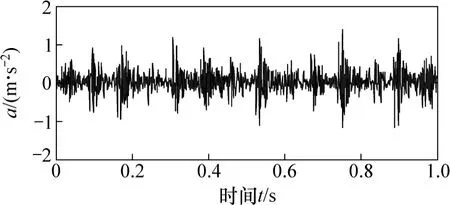
图2 轴承内圈振动时域信号Fig. 2 Time-domain fault vibration signal of inner race
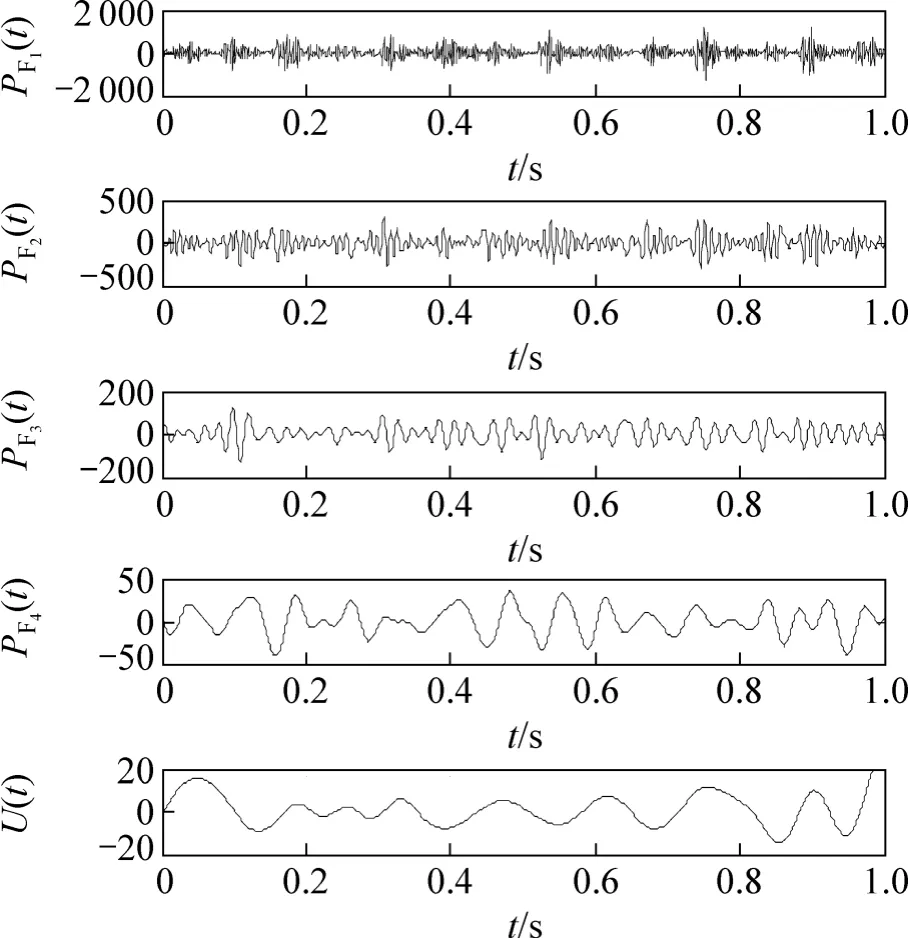
图3 故障振动信号的LMD分解结果Fig. 3 LMD decomposes results of inner race fault vibration signals
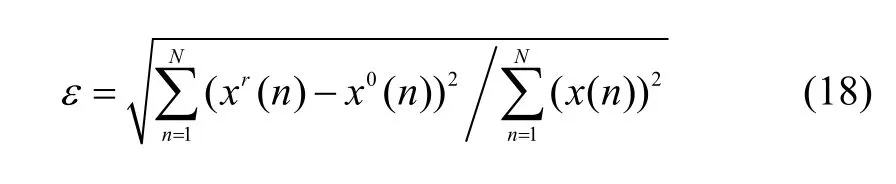
式中:N为信号采集点数。
考察不同压缩比(R=M/N,N为采样点)下,信号重构精度的变化。改变测量值次数M,分别取768,512,384和256,通过仿真计算重构相对误差结果如表1所示。
由表1可以看出:在同一频段、同一变换基下,随着测量数减少,重构精度降低,相对误差增大,其中高频分量较低频分量,计算复杂度高且重构相对误差也大;随着频率的降低,重构相对误差越来越小,PF3-U(t)分量在3种压缩比情况下相对误差较小,因为 LMD在分解信号过程中, PF3-U(t)信号频率越来越低,逐渐平稳,在快速傅里叶变换基(FFT)下的稀疏度越来越好,在测量次数很低的情况下,当压缩比 R为1/4时, PF3, PF4和U(t)的信号重构相对误差平均值也仅为0.271 3。
从测量次数来看,随着测量次数的减少,各个分量的重构相对误差在增加,由于信号被压缩的程度越来越大,因此,所采集到的信息便越来越少,相对误差也就变大。

表1 不同压缩比情况下各乘积函数(PF分量)的重构相对误差比较Table 1 Reconstruction relative error comparison of each PF component under different compression ratios
从各压缩比信号重构相对误差的平均值来看,考虑既要达到很好的压缩比,减少数据存储量,提高传输效率的目的,又要控制重构信号的相对误差要求。因此,选择 M=512,压缩比为 1/2,信号重构平均相对误差为0.290 5;信号各PF分量进行组合得到的重构信号,各PF分量及其重构效果如图4所示。图5所示为重构 PF后最终输出信号与原始振动信号及误差对比图,计算得重构误差为0.513 7。保留其他参数不变,对信号进行直接非凸罚最小化Lq正则子CS处理,得到重构信号及其误差如图6所示,计算得到重构误差为0.707 3。
由图5和图6可以看出:采用LMD分解与非凸罚最小化 Lq正则子重构算法相结合的方法重构的信号的效果比直接运用CS理论重构的信号的效果要好,重建结果与原始信号的特征变化不大,采用 LMD与非凸罚最小化Lq正则子重构算法信号重构精度更高,且随着重构采样点的增多,效果会更加明显。

图4 振动信号各PF分量信号、各重建信号幅值及其误差Fig. 4 Every PF component signal amplitude, reconstruction signal amplitude and their reconstruction errors
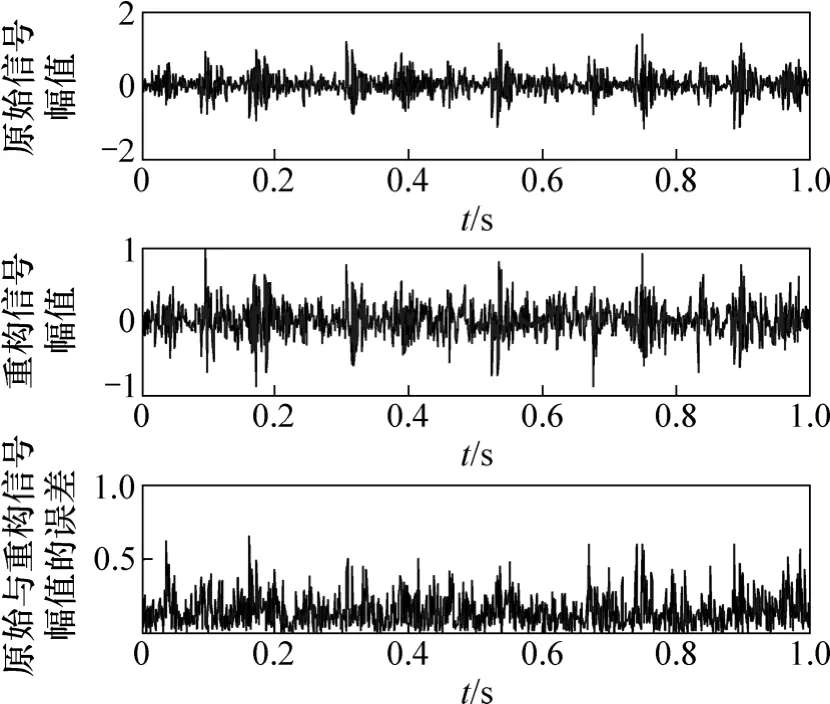
图5 原始信号幅值、重构的最终输出信号幅值及其误差Fig. 5 Original vibration signal amplitude, reconstruction signal amplitude and their reconstruction errors
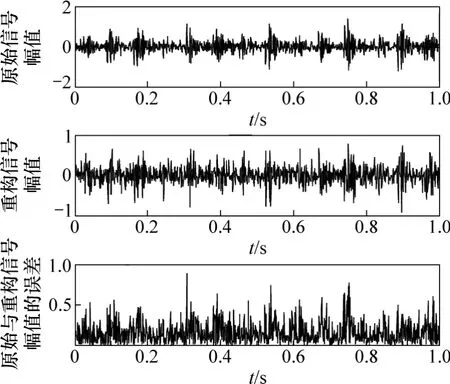
图6 原始信号幅值、直接重建信号幅值及其误差Fig. 6 Original vibration signal amplitude, direct reconstruction signal amplitude and their reconstruction errors
4 结论
1) LMD方法能够根据信号自身的时间尺度特征自适应将轴承故障振动信号分解为若干个PF分量,每个PF分量由1个包络信号和1个纯调频信号组成。
2) 仿真验证表明在压缩传感过程中,非凸罚最小化 Lq正则子(q=0.5)重构算法相对其他重构优化算法具有很高的重构精度。
3) 针对不同频段的 PF分量特征采用不同的稀疏基进行稀疏表示,用非凸罚最小化 Lq正则子(q=0.5)重构算法合并得到的输出振动信号重构精度优于直接对振动信号压缩传感得到的信号重构精度。
[1] Vijaya C, Bhat J S. Signal compression using discrete fractional Fourier transform and set partitioning in hierarchical tree[J].Signal Processing, 2006, 86(8): 1976-1983.
[2] Alkishriwo O A, Chaparro L F. Signal compression using the discrete linear chirp transform (DLCT)[C]//IEEE International Conference on Signal Processing. Bucharest, Romania, 2012:2128-2132.
[3] Oltean M, Picheral J, Lahalle E, et al. Compression methods for mechanical vibration signals: Application to the plane engines[J].Mechanical Systems and Signal Processing, 2013, 41(1):313-327.
[4] 杜金榜, 王跃科, 潘仲明, 等. 旋转机械振动数据压缩及语音压缩技术的应用研究[J]. 计算机测量与控制, 2006, 14(12):1594-1596.DU Jinbang, WANG Yueke, PAN Zhongming, et al. Vibration data compression of rotary machines and application of speech compression technology[J]. Computer Measurement and Control,2006, 14(12): 1594-1596.
[5] 石光明, 刘丹, 高大化, 等. 压缩感知理论及其研究进展[J].电子学报, 2009, 37(5): 1070-1081.SHI Guangming, LIU Dan, GAO Dahua, et al. Advances in theory and application of compressed sensing[J]. Acta Electronic Sinica, 2009, 37(5): 1070-1081.
[6] 李波, 谢杰镇, 王博亮. 基于压缩传感理论的数据重建[J]. 计算机技术与发展, 2009, 19(5): 23-25.LI Bo, XIE Jiezhen, WANG Boliang. Signal reconstruction based on compressed sensing[J]. Computer Technology and Development, 2009, 19(5): 23-25.
[7] Candes E J, Wakin M B. An introduction to compressive sampling[J]. Signal Processing Magazine, 2008, 25(2): 21-30.
[8] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[9] Candes E J, Romberg J, Tao T. Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006,52(2): 489-509.
[10] Dybala J, Zimroz R. Rolling bearing diagnosing method based on Empirical mode decomposition of machine vibration signal[J].Applied Acoustics, 2014, 77(3): 195-203.
[11] Smith J S. The local mean decomposition and its application to EEG perception data[J]. Journal of the Royal Society Interface,2005, 2(5): 443-454.
[12] ZHANG Hai, WANG Yao, CHANG Xiangyu, et al. L1/2regularization[J]. Science China, 2010, 40(3): 412-422.
[13] Candes E J, Romberg J. Quantitative robust uncertainty principles and optimally sparse decompositions[J]. Foundations of Compute Math, 2006, 6(2): 227-254.
[14] Candes E J, Romberg J. Sparsity and incoherence in compressive sampling[J]. Inverse Problems, 2007, 23(3): 969-985.
[15] Donoho D L, Tsaig Y. Extension of compressed sensing[J].Signal Processing, 2006, 86(3): 549-571.
[16] Candes E J, Tao T. Near optimal signal recovery from random projections: Universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425.
[17] Baraniuk R, Steeqhs P. Compressive radar imaging[C]//IEEE International Conference on National Radar Conference Proceedings. Boston, USA, 2007: 128-133.
[18] LAI Mingjun, XU Yangyang, YIN Wotao. Improved iteratively reweighted least squares for unconstrained smoothed Lqminimization[J]. SIAM Journal on Numerical Analysis, 2013,51(2): 927-957.
[19] Candes E J, Romberg J. L1-magic: Recovery of sparse signals via convex programming[D]. California: Caltech. School of Engineering & Applied Science, 2005: 1-11.
[20] Candes E J, Romberg J, Tao T. Stable signal recovery from incomplete and inaccurate measurements[J]. Communications on Pure and Applied Mathematics, 2006, 59(8): 1207-1223.
[21] Candes E J, Wakin M B, Boyd S P. Enhancing sparsity by reweighted minimization[J]. Journal of Fourier Analysis and Applications, 2008, 14(5): 877-905.
[22] Salman A M, Romberg J. Dynamic updating for L1minimization[J]. IEEE Journal on Selected Topics in Signal Processing, 2010, 4(2): 421-434.
[23] Foucart S, LAI Mingjun. Sparsest solutions of underdetermined linear systems via Lq-minimization for 0<q<1[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 395-407.
