双节悬臂管流固耦合系统基座振动研究
王斌华
(长安大学 道路施工技术与装备教育部重点实验室,西安 710064)
管道流固耦合振动问题蕴含丰富、复杂的动力学内容而备受关注,研究其振动特性具有广泛的工程背景及重要应用价值。目前,对悬臂管流固耦合系统振动研究大多局限于单节臂管道振动特性[1],或虽考虑多节臂管道振动,但仅研究刚性输液管道耦合系统[2],未考虑管道弹性变形对耦合系统的动力学影响。工程应用中,如喷浆机、混凝土泵车及高空消防车等均采用流体输送管道附在多节柔性臂的结构设计,且节臂系统常位于振动基础上,因此开展多节悬臂管流固耦合系统基座振动分析有重要工程价值。已有对此类机械多节臂杆结构的动力学研究[3-4]及振动控制研究[5-7],但模型中未考虑流固耦合与基座振动因素。
本文结合柔性多体动力学[8-9]与流固耦合动力学理论,利用悬臂输液管Lagrange方程建立基座振动作用时双节柔性悬臂管流固耦合系统动力学方程,分析节臂姿态变化、节臂长度及平均流速对流固耦合系统振动影响。
1 耦合系统运动微分方程
双节悬臂管流固耦合系统基座振动模型见图1。方程建立基于假设:每节悬臂管全长范围内具有统一内径及截面属性,材料各向同性;已知悬臂管材料弹性模量 E,截面惯性矩 I1、I2,单位长度质量 ρp1、ρp2,管长l1、l2;管内为无粘不可压缩液体,液体单位长度质量ρf1、ρf2;流速U(t),任一点流体流速方向相切于该处弹性变形管轴线,平行于单位切矢量;忽略流体-悬臂管系统内外结构阻尼及悬臂管剪切变形;悬臂管振动时管轴线不可伸长。悬臂管位于竖向振动基础上,建立绝对坐标系x0o0y0与连体坐标系xioiyi( i=1,2,3),o1点竖向振动位移为v(t),x1o1y1固定于振动基础上,悬臂管1管单元产生沿x2轴、y2轴位移分别为u1、w1,悬臂管2的管单元产生沿x3轴、y3轴位移分别为u2、w2。

图1 双节悬臂管流固耦合系统基座振动模型Fig.1 Dynamic model of the two cantilever pipes on vibration foundation
由图1(b)可知,坐标系x2o2y2中,悬臂管1上任意管单元p1位置矢量为

在坐标系x0o0y0中,悬臂管1上任意管单元p1位置矢量为
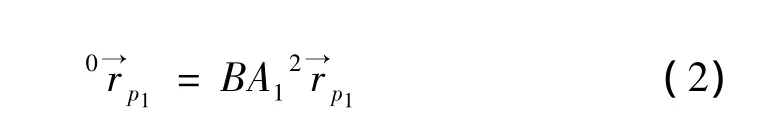
管单元p1速度矢量为
式中:B为从连体坐标系x1o1y1到绝对坐标系x0o0y0的平移变换矩阵;A1为动坐标系 x2o2y2到动坐标系x1o1y1的方向余弦矩阵,即

式中:β1为x2轴与x1轴夹角。
坐标系x0o0y0中悬臂管1内流体单元速度矢量为

式中:2τ→f1为流体单元在坐标系x2o2y2中的切矢量,即
悬臂管2上管单元速度矢量为



式中:β2为坐标系x3o3y3的x3轴与坐标系x1o1y1的x1轴夹角。
在坐标系x0o0y0中,悬臂管2内流体单元的速度矢量为

式中:3τ→f2为流体单元在坐标系x3o3y3中切矢量,即
因此,悬臂管1动能为

悬臂管1势能为

悬臂管1内流体动能为


悬臂管1内流体势能为

悬臂管2动能为

悬臂管2势能为

悬臂管2内流体动能为

悬臂管2内流体势能为

用假设模态法,两节柔性臂在各自连体坐标系横向位移可表示为里兹基函数的线性组合[10-11],即

式中:qkr(t)为对应φkr(x)的广义坐标,φkr(x)为k节臂杆r阶基函数;N为里兹基函数阶数,据研究对象的固有频率、激扰频率确定此处N=2即可获得满意的近似。前两阶基函数[12]为

据文献[1],悬臂输液管系统Lagrange方程为

式中:→r 为悬臂管末端位置矢量(图1(a)),即
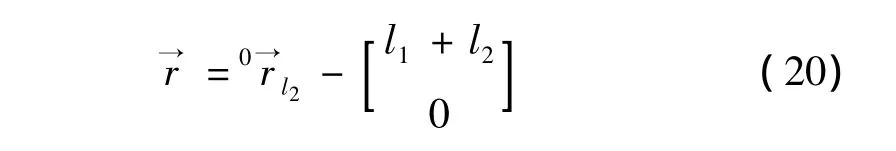
且

将式(9)~式(16)及式(20)、(21)代入式(19),采用里兹基函数线性化表示节臂的横向变形,整理得悬臂管流固耦合动力学方程为

式中:M,C,K,F分别为质量、阻尼、刚度矩阵及载荷列阵;q为广义坐标列阵。
对时变系数微分方程组一般采用逐步积分的数值方法求解,本文用Newmark-β法,用MATLAB编写程序,通过数值计算求得任意时刻广义坐标q(t),代入式(17)即可获得悬臂管动态响应。
2 数值仿真
双节悬臂管参数为:臂长l1=l2=0.75 m,节臂1惯性矩 Ip1=5.208 ×10-10m4,节臂2 惯性矩 Ip2=3.125×10-10m4,节臂1 密度 ρp1=0.675kg/m,节臂 2 密度ρp2=0.405kg/m,弹性模量 E=6.895 ×1010Pa,流体密度 ρf1= ρf2=0.154kg/m。
选取节臂的3种姿态进行振动响应分析,姿态角分别为:姿态1(β1=0°,β2=0°),姿态 2(β1=52°,β2=-28°),姿态3(β1=80°,β2=0°)。
2.1 流体平均流速影响分析
基座振动位移为 v(t)=0.0015 sin(0.6πt)(m),选取流体流速分别为 U1(t)=2+0.1sin(0.6πt)(m/s)、U2(t)=5+0.1sin(0.6πt)(m/s)及 U3(t)=10+0.1sin(0.6πt)(m/s)进行分析,结果见图3。由图3可知,①平均流速相同时节臂系统姿态变化使系统振动响应变化较大,说明姿态角变化对双节悬臂管流固耦合系统影响显著;②节臂系统姿态不变时,随平均流速增加姿态1动态响应幅值逐渐减小,姿态2、3动态响应幅值减小后再增大,但平均流速的提高会增加流体流动产生的激励作用,使3种姿态的振动响应均值提高,且对水平姿态1可达较高的工作流速不使振动响应幅值过大。

图3 不同平均流速时节臂振动响应Fig.3 Vibration response of arms with different flow velocity
2.2 节臂长度影响分析
基座振动位移为 v(t)=0.0015 sin(0.6πt)(m),选取节臂长度参数分别为:① 臂长参数1(L1=0.5 m,L2=1.0 m);② 臂长参数2(L1=0.75 m,L2=0.75 m);③ 臂长参数 3(L1=1.0 m,L2=0.5 m),姿态变化后节臂动态响应见图4。由图4可知,① 在每种固定姿态下,改变节臂长度使其末端振动响应变化显著。因节臂长度变化会改变振动系统质量分布,引起系统固有频率变化,因此振动响应幅值、频率均发生变化;② 由图4(b)知,L1=1.0 m,L2=0.5 m 时节臂间弯矩振动幅值最小。因此,采用节臂间弯矩作为主动控制力时该系统所需控制力较小,说明进行节臂系统振动控制设计时,优化臂架长度可降低系统控制能量。

图4 不同节臂长度时节臂振动响应Fig.4 Vibration response of arms with different arm length
3 试验研究
为验证理论模型的正确性,在振动台上进行双节悬臂管流固耦合系统动态响应试验,对比研究节臂2末端实测振动加速度与仿真计算值。为控制设定的基座振动参数,将双节悬臂管模型夹持在SDS-500型液压伺服动静试验机上,由工控机控制伺服油缸振动位移为 v(t)=0.0015 sin(0.6πt)(m),加速度传感器选ARF-20A,采集系统为DH5927。通过定量泵控制流速为U=3.82 m/s。试验照片见图5,试验、仿真结果对比见图6。由图6对比分析可知,姿态变化时测试曲线与仿真曲线的峰谷出现时刻基本对应,且曲线变化规律及幅值基本相同,说明该理论模型合理。

图5 试验照片Fig.5 Test photos

图6 加速度计算与测试结果对比图Fig.6 Acceleration results comparison between calculation and test
4 结论
基于柔性多体动力学与流固耦合动力学理论,利用悬臂输液管Lagrange方程建立双节悬臂管流固耦合系统基座振动力学方程,研究节臂姿态、平均流速及节臂长度对流固耦合系统振动影响。结论如下:
(1)节臂姿态与长度变化对双节悬臂管流固耦合系统振动响应影响显著。
(2)提高平均流速可增加流体产生的激励作用,提高双节悬臂管流固耦合系统振动响应均值,且对水平姿态,具有较高的稳定工作流速。
(3)节臂长度变化影响节臂2约束端振动弯矩,因此进行节臂系统振动控制设计时,优化臂架长度可降低系统控制能量。
(4)通过双节悬臂管流固耦合系统振动台试验与仿真分析对比,验证所建动力学模型的正确性,该模型可用于双节悬臂管系统主动控制研究。
[1]Païdoussis M P.Fluid-structure interactions (slender structures and axial flow)VolⅠ[M].London:Academic Press,1998.
[2]Paidoussis M P ,Deksnis E B.Articulated models of cantilevers conveying fluid:the study of a paradox[J].Journal of Mechanical Engineering Science,1970,12(4):288-300.
[3]刘杰,戴丽,赵丽娟,等.混凝土泵车臂架柔性多体动力学建模与仿真[J].机械工程学报,2007,43(11):131 -134.LIU Jie, DAI Li, ZHAO Li-juan,et al. Modeling and simulation of flexible multi-body dynamics of concrete pump tuck arm[J].Chinese Journal of Mechanical Engineering,2007,43(11):131 -134.
[4]Cazzulani G,Ghielmetti C,Giberti H,et al.A test rig and numerical model for investigating truck mounted concrete pumps[J].Automation in Construction,2011,20(8):1133-1142.
[5]黄毅,吴斌兴,王佳茜.混凝土泵车臂架振动响应的主动控制实验研究[J].振动与冲击,2012,31(2):91-94.HUANG Yi,WU Bin-xing,WANG Jia-qian.Test for active control of boom vibration of a concrete pump truck[J].Journal of Vibration and Shock ,2012,31(2):91 -94.
[6]Resta F,Ripamonti F,Cazzulani G,et al.Independent modal control for nonlinear flexible structures:an experimental test rig[J].Journal of Sound and Vibration,2010,329(8):961-972.
[7]Bagordo G, Cazzulani G, Resta F, et al. A modal disturbance estimator for vibration suppression in nonlinear flexible structures[J].Journal of Sound and Vibration,2011,330(25):6061-6069.
[8]王相兵,童水光.基于刚柔耦合的液压挖掘机机械臂非线性动力学研究[J].振动与冲击,2014,33(1):63-70.WANG Xiang-bing,TONG Shui-guang.Nonlinear dynamical behavior analysis on rigid-flexible coupling mechanical arm of hydraulic excavator[J].Journal of Vibration and Shock,2014,33(1):63 -70.
[9]陆佑方.柔性多体系统动力学[M].北京:高等教育社,1996:1 -30,233 -266.
[10]Abe A.Trajectory planning for residual vibration suppression of a two-link rigid-flexible manipulator considering large deformation[J].Mechanism and Machine Theory,2009,44(9):1627-1639.
[11]蒙树立,熊静琪,吕志刚.折叠式高空作业车臂架系统的动力学建模[J].噪声与振动控制,2012,32(4):63 -67.MENG Shu-li,XIONG Jing-qi,LÜ Zhi-gang.Modeling of arm system of folding-boomaerial platform vehicle[J].Noise and Vibration Control,2012,32(4):63 -67.
[12]Gorman D G, Trendafilova I, Mulholland A J,et al.Analytical modelling and extraction of the modal behaviour of a cantilever beam in fluid interaction[J].Journal of Sound and Vibration,2007,308:231-245.

