基于粒子滤波的TBD算法研究

边 旭,李江勇

(华北光电技术研究所，北京 100015)

基于粒子滤波的TBD算法研究

边 旭,李江勇

(华北光电技术研究所，北京 100015)

结合粒子滤波算法基本理论与弱小目标检测问题建立了目标运动与量测模型。针对传统粒子滤波算法存在的问题提出了一种基于分步采样与改进重采样的新型算法,通过软件生成测试图像对算法进行仿真研究,实验结果表明算法具有较高的检测性能并且算法复杂度较低。

粒子滤波;TBD;重要性概率密度;贝叶斯估计;分步采样;重采样

1 引 言

现代战争中,红外探测系统以其较强的抗干扰能力、隐蔽性好等特点逐渐受到人们的重视。多年来,广大研究人员采用各种手段提高其探测性能,其中提高目标检测算法性能尤其是弱小目标的检测性能是一项重点研究内容,可以弥补红外探测系统作用距离短的不足。鉴于红外弱小目标图像的低信噪比特征,一种称为先跟踪后检测(TBD)的检测方法正逐步取代传统DBT算法成为主流发展方向[1]。基于粒子滤波的TBD算法对目标的运动形式没有限制,并且允许动态噪声和量测噪声是非高斯的,因此成为时下比较热门的研究方向。

在深入研究粒子滤波基本理论与典型步骤的前提下,提出了一种基于分步采样的检测算法,并在重采样过程中提出一种新型的大权重粒子分裂方法,以改进传统重采样算法中直接复制粒子带来的样本匮乏。通过这两种新方法的结合,不仅降低了粒子滤波算法的复杂度,而且保持了粒子的多样性。最后通过仿真实验验证了本文算法的优越性。

2 粒子滤波算法的引出过程与存在问题

弱小目标的检测与跟踪任务可看成为一种动态系统状态估计问题[2],在此框架下,粒子滤波的引出过程如图1所示。

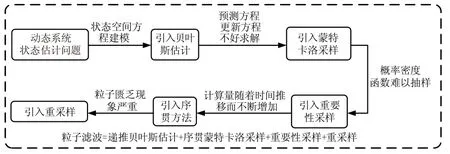
图1 粒子滤波理论的引出过程

在上述过程中存在两个问题,一是重要性概率密度函数不好选择,二是重采样算法带来的样本匮乏现象严重。学者们主要通过两种手段来改进。其一是选择较好的重要性密度函数,代表算法有 PF-EKF,PF-UKF,PF-IEKF,PF-IUKF和高斯-厄米特粒子滤波等[2]。它们使用某些运算量较小次优滤波器的输出结果作为重要性密度,由于考虑了最新的观测,因而比基本粒子滤波单纯采用系统状态转移概率作为重要性密度性能要优越。其二是改进重采样算法,增加粒子群的多样性,代表算法有MCMC移动步骤、遗传算法重采样、裂变自举粒子滤波等[3]。

3 改进粒子滤波算法

3.1 改进算法描述

鉴于传统的粒子滤波算法存在的问题,本文主要从两个方面改进。

表1 本文算法改进点描述

3.2 算法步骤

结合红外弱小目标运动量测模型与TBD问题模型,本文提出基于分步采样与改进重采样方法的粒子滤波步骤：

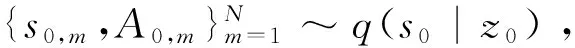
(2)K>0时刻

按马尔科夫链的概率转移矩阵得到粒子状态Ak,m～p{Ak-1,m,ΠA}。其中,Ak∈{0,1},0表示目标不存在,1表示存在。

其中,Pb为目标出现概率;Pd为目标消失概率[5]。

a)对于新生粒子(Ak-1,m=0,k,m=1),取样一般按服从均值为状态值的高斯分布采样。

b)对于延续粒子(Ak-1,m=1,k,m=1),取样sk,m～q(sk|sk-1,zk),概率密度函数一般选为状态方程sk=Fsk-1+ωk,其中ωk为零均值高斯白噪声。这一步按照分步采样方法,只进行位置信息与强度信息的采样更新,速度信息仍然使用初始值。

(3)按照以下公式计算粒子权值：

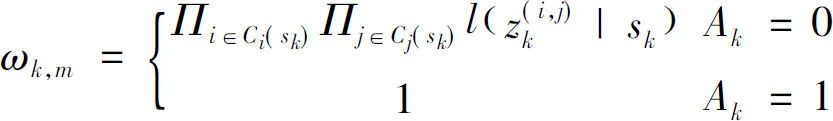
通过推导可得:

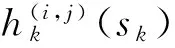
(4)归一化权值:

(5)改进重采样。首先通过计算每个粒子的权重与1/N的比值(小数要化为整数)来得到粒子的复制次数n。n=0的粒子直接剔除,n=1的粒子直接复制,n>1的粒子按高斯分布采样得(n-1)个粒子,权重设为1/N。

(6)计算k时刻检测与跟踪结果。

(a)按下式计算目标出现概率：

当pk>Th(Th为预设门限)则判定目标存在。

(b)按下式计算目标状态估计：

k=k+1,转步骤(2)。

算法步骤流程图如图2所示。

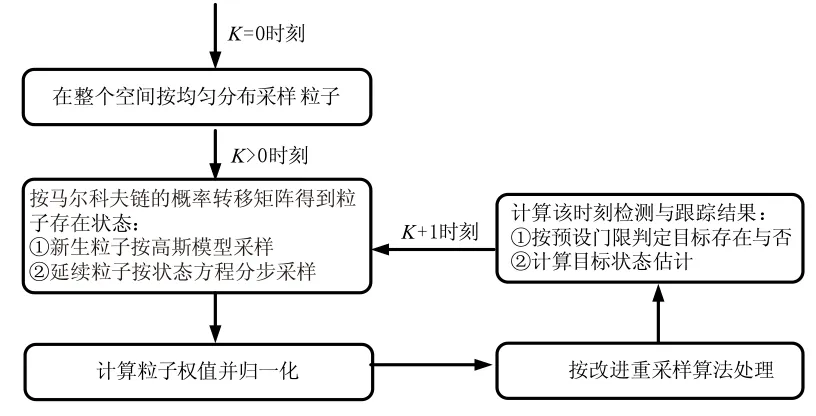
图2 算法步骤流程图

4 仿真实验与结果分析

本算法仿真实验硬件平台为Intel(R)Core(TM)2DuoCPUE8200 2.66GHz。软件为MATLAB2011a。

在MATLAB上生成30帧测试图像。相关参数设置为：

像元尺寸Δx=Δy=1,图像大小nx=my=200,观测周期T=1,目标信号强度设为I=20,传感器模糊程度Σ=0.7。设目标出现的帧数为第7帧,一直存在15帧,在第23帧消失。目标初始状态设为s0=[78,0.45，92,0.25,20],目标运动噪声q1=0.001,目标强度噪声q2=0.01。观测噪声方差σ决定了信噪比SNR的大小,它们之间的关系可表示如下：

本文在四种信噪比下验证算法,SNR分别取为2dB、5dB、10dB和15dB,对应的σ分别为5.1601、3.6530、2.0543和1.1552。

图3(a)、(b)分别为信噪比为15dB时第6帧和第10帧的仿真图像。

初始时刻目标状态在整个空间均匀采样：

位置x～U[0,nx],y～U[0,my]

强度I～U[10,30]。

图3 仿真图像

仿真实验分别在四种信噪比下对本文提出的改进粒子滤波方法与传统的粒子滤波方法进行比较。传统的粒子滤波算法采取的粒子数分别为20000、10000、5000,本文提出的算法选取粒子数5000,图4(a)、(b)分别是信噪比为15dB与2dB不同条件下得出的检测概率曲线。

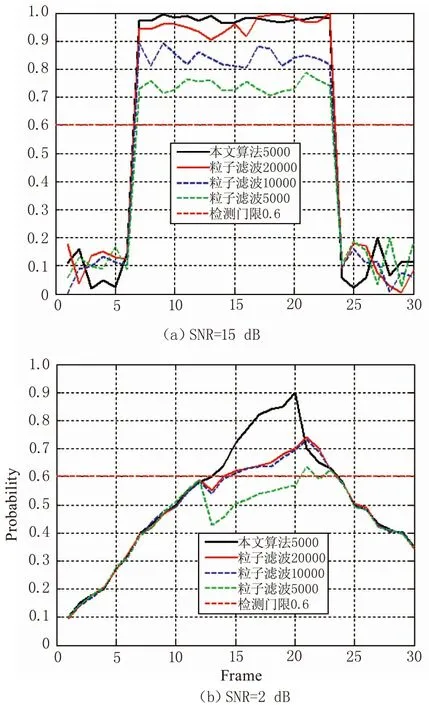
图4 不同条件下的检测概率曲线

可以看出,当信噪比为15dB时,两种算法都没有目标出现检测延迟和目标消失检测延迟,并有很好的检测能力。当信噪比为2dB时,出现了检测延迟。但是,无论在哪种信噪比下,本文提出的改进的粒子滤波算法都要比传统算法有着较高的检测概率,即使传统算法的粒子数选取为本文算法的四倍时这种现象仍然很明显。

表2为两种算法的运算时间对比。可以看出本文算法比传统算法节省了大量时间。当传统算法粒子数为20000时才能取得较好的检测效果,但是它用去的时间是本文算法的10倍以上,而且其检测性能低于本文算法。

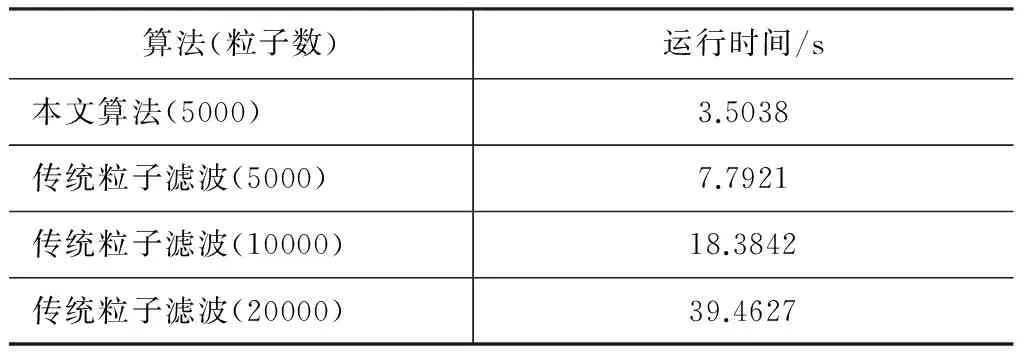
表2 两种算法运算时间

通过上面的实验结果可知本文算法检测性能相对于传统算法有很大的提升,算法复杂度也比传统算法减弱了不少。

5 结 语

在深入研究粒子滤波基本原理的基础上,提出了分步采样与改进重采样相结合的新型粒子滤波算法。并基于红外弱小目标检测问题建立了粒子滤波TBD模型,利用MATLAB仿真平台生成测试图像并按照改进的粒子滤波步骤进行仿真实验研究,最后得出的实验结果很好的体现了本文算法的优越性。下一步的研究还应该继续深入,考虑粒子滤波中另一个重要问题——重要性概率密度的选择,提出相应的改进算法,并在本文单目标检测的基础上开始研究多目标的检测与跟踪问题。

[1] ZHANG Changcheng,YANG Degui,WANG Hongqiang.Algorithm surveys for dim targets track-before-detect in infrared image[J].Laser & Infrared，2007,37(2):104-107.(in Chinese) 张长城,杨德贵,王宏强.红外图像中弱小目标检测前跟踪算法研究综述[J].激光与红外，2007,37(2):104-107.

[2] ZHU Zhiyu.Particle filters algorithm and its application[M].Beijing:Science Press,2010.(in Chinese) 朱志宇.粒子滤波算法及其应用[M].北京：科学出版社，2010.

[3] Efthimios E Tsakonas,Nicholas D Sidiropoulos.Optimal particle filters for tracking a time-varying Harmonic or chirp signal[M].IEEE Transactions on Signal Processing,2008,56:4598-4610.

[4] CHEN Xi.Research on track-before-detect algorithm based on particle filter[D].Xi′an:Xidian University,2009.(in Chinese) 陈曦.基于粒子滤波的检测前跟踪算法研究[D].西安:西安电子科技大学.2009.

[5] GONG Yaxin,YANG Hongwen,et al.Multiple model particle filter based track-before-detect for maneuvering weak target[J].Journal of Electronics & Information Technology,2008,30(4):941-944.(in Chinese) 龚亚信,杨宏文，等.基于多模粒子滤波的机动弱目标检测前跟踪[J].电子与信息学报,2008,30(4):941-944.

[6] FANG Wentao,WANG Xiangjun,TANG Qijian.Object tracking system for MUAV Based on particle filter[J].Laser & Infrared,2012,42(7):841-844.(in Chinese) 房文涛，王向军，汤其剑，等.基于粒子滤波的机载目标跟踪系统设计[J].激光与红外,2012,42(7):841-844.

Research on Track -Before-Detect algorithm based on particle filter

BIAN Xu,LI Jiang-yong

(North China Research Institute of Electro-optics, Beijing 100015, China)

Combined the basic theory of particle filter algorithm with the small targets detection methods, the models of moving targets and measurement were established. Aiming at the issue of traditional particle filter algorithm, a new algorithm based on two-level sampling and improved re-sampling is proposed. The algorithm was simulated by the software Matlab. The experiment results show that the algorithm has good performance and simple calculation.

particle filter;TBD;essentiality PDF;Bayesian estimation;two-level sampling;re-sampling

1001-5078(2015)01-0109-04

边 旭(1989-)，男，硕士研究生，主要研究方向为光电探测技术。E-mail：814100466@qq.com

2014-07-09;

2014-08-11

TP391.41

A

10.3969/j.issn.1001-5078.2015.02.024