基于判别信息的近邻保持嵌入降维方法
张海武, 陈晓云
(福州大学数学与计算机科学学院, 福建 福州 350116)
基于判别信息的近邻保持嵌入降维方法
张海武, 陈晓云
(福州大学数学与计算机科学学院, 福建 福州 350116)
针对传统近邻保持嵌入算法(NPE)侧重保持样本的局部结构, 而没有考虑样本类别信息的不足, 提出判别局部近邻保持嵌入算法DLNPE. 该算法利用样本点的局部结构构造新定义下的类内类间散布矩阵, 并以此作为判别信息引入目标函数. 在6个真实数据上进行实验, 证明了所提算法的有效性.
降维; 近邻保持嵌入; 判别信息; 局部结构
0 引言
在各种降维方法中, 线性降维方法如主成分分析(principal component analysis, PCA)[1]和线性判别分析(linear discriminant analysis, LDA)[2]因其简单有效而被广泛使用. 但这些线性方法具有难以保持原始数据非线性流形的缺点. 为此, 研究人员提出流形降维算法如等容特征映射(isometric feature mapping, ISOMAP)[3]、 拉普拉斯特征映射(laplacian eigenmap,LE)[4]、 局部线性嵌入(locally linear embedding,LLE)等[5]. 这些算法在处理非线性结构数据时可以获得较好结果. 然而它们都有一个共同问题, 即在高维观测空间和内在低维空间之间建立的隐式映射是定义在训练集上, 无法处理新来样本问题. 为克服上述缺点, He等[6]人提出近邻保持嵌入算法(neighborhood preserving embedding,NPE). 尽管NPE的改进是有效的, 但它没有考虑样本的类别信息, 是一种无监督降维方法. 于是, 王国强等[7]受LDA方法启发, 在NPE基础上引入全局判别信息, 提出保持近邻判别嵌入算法(neighborhood preserving discriminant embedding, NPDE). 但NPDE引入的全局判别信息具有对噪声敏感, 易受样本分布影响的缺点.
基于NPE和NPDE算法的不足, 提出判别局部近邻保持嵌入算法(DLNPE). 该算法对局部结构中邻域样本的类别进行区分, 引入有效判别信息. 在嵌入低维空间后, 类内样本保持固有的近邻几何结构, 且类间样本彼此分离. 为验证所提DLNPE算法的有效性, 将其应用于6个真实数据上, 并与NPDE、 DLPP、 NPE和LPP这4种方法进行对比.
1 近邻保持嵌入算法及相关研究
1.1 近邻保持嵌入(NPE)[6]
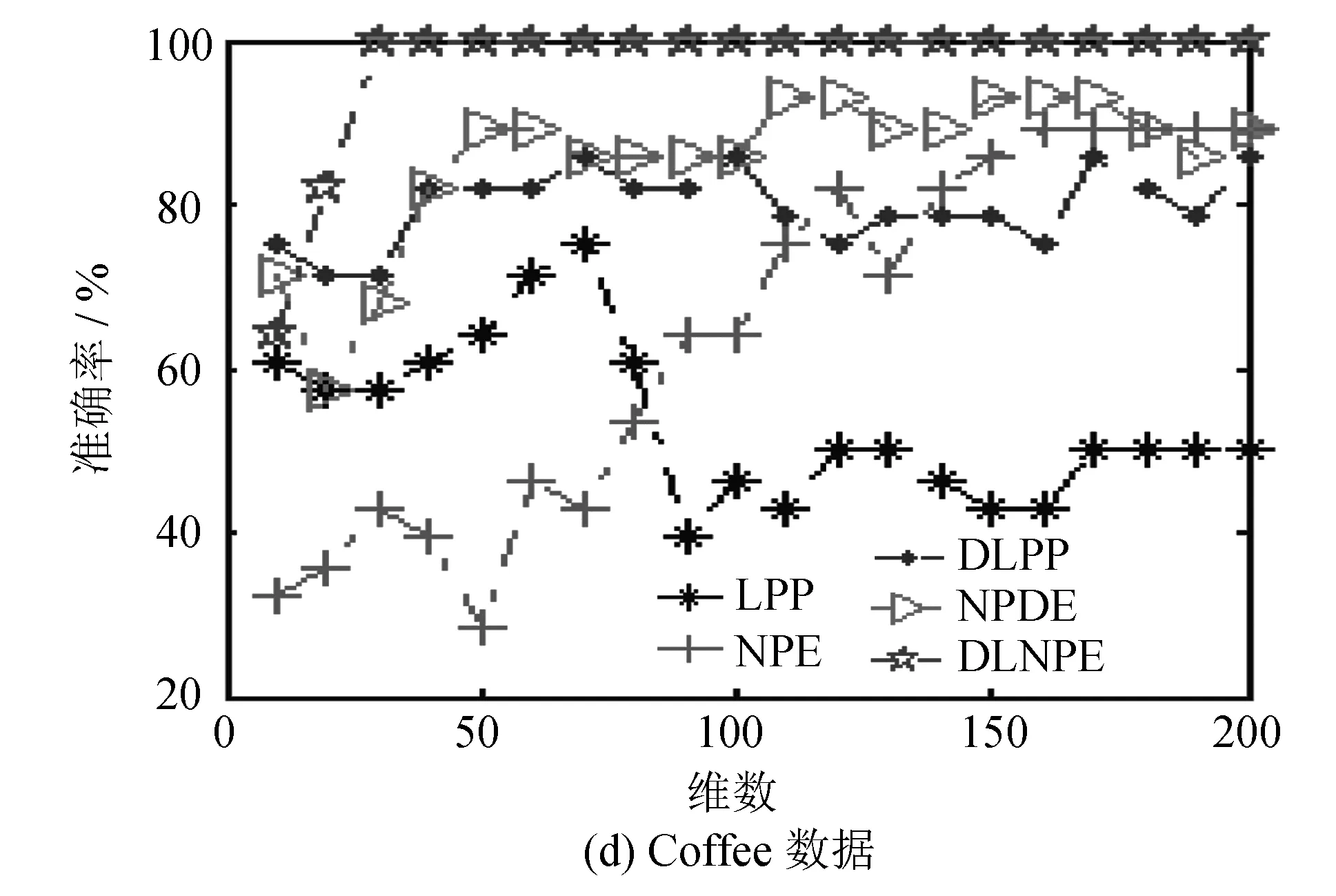
假设X=(x1,x2, …,xn)是由n个样本所组成的数据集, 每个样本维数为m. 找到一个投影变换矩阵A, 将数据集映射到一个低维空间Rd(d 近邻保持嵌入算法(NPE)是一种无监督降维方法, 能够保持近邻样本点间的局部结构. 它对每个数据点用其k近邻进行线性重构. 用yij(j=1, 2, …,k)表示yi的k近邻点,wij表示yi和yj之间的权值, 令权重矩阵为W, 那么NPE的目标函数为: 其中:M=(I-W)T(I-W), 变换矩阵A可以通过求解以下的最小化问题得到: 1.2 保持近邻判别嵌入(NPDE) 保持近邻判别嵌入算法(NPDE)[7]充分利用判别信息, 既保持同类样本的领域结构, 又使得不同类样本的平均嵌入向量相互分离. 该算法的目标函数定义如下: 其中:M′=diag(M1,M2, …,Mc),Mc=(I-Wc)T(I-Wc);F=[f1,f2, …,fc],fi是第i类样本均值;G=(I-B)T(I-B),I是单位矩阵. NPE是一种无监督降维方法, 没有考虑样本的类别信息. 受到半监督局部线性判别算法(SELF)[8]启发, 本文在NPE基础上, 引入新定义下的类间散布矩阵S(rlb)和类内散布矩阵S(rlw)作为判别信息, 其定义如下: 式(9)、 (10)中sij为样本xi和xj的相似度,Nci为第ci类样本总数.ci=cj表示样本xi和xj属于同一类,ci≠cj表示样本xi和xj属于不同类. 在计算S(lb)时, 若ci=cj则赋予负数权重; 若ci≠cj则赋予权重为1/n. 在计算S(lw)时, 若ci=cj则赋予较大权重; 若ci≠cj则赋予较小权重0. 这体现了类间最大化, 类内最小化的思想. 本文引入S(rlb)-S(rlw)作为判别信息, 将引入判别信息后的算法称为判别局部近邻保持嵌入算法(DLNPE), 其目标函数为: 对上式分子进行化简: 则DLNPE的目标函数可以简化为: 那么, 求解变换矩阵的最小化问题为: 使目标函数最小化的变换矩阵可以通过求解广义特征向量得到: 若α1,α2, …,αd为上式前d个广义特征值λ1≤λ2≤ … ≤λd所对应的特征向量, 那么最优投影矩阵A可表示为A=(α1,α2…αd). 下面给出DLNPE算法的具体描述: 算法名称: 判别局部近邻保持嵌入算法(discriminantlocalneighborhoodpreservingembedding,DLNPE) 输入: 数据集X, 权重参数β, 近邻参数k, 子空间维数d. 输出: 降维后的数据mappedX. Step 1: 进行PCA投影, 避免高维小样本问题, 为了方便起见, 将投影后的数据集仍记为X(若数据集为非高维小样本数据可省略Step 1); Step 2: 与NPE算法类似, 计算近邻重建权重矩阵W; Step 3: 计算XMXT的值, 并记为Q; Step 4: 计算新定义下的类内散布矩阵S(rlw)和类间散布矩阵S(rlb), 并计算S(rlb)-S(rlw)的值, 记为P; Step 5: 解广义特征值问题Qα=λPα, 求出前d个广义特征值λ1≤λ2≤…≤λd所对应的特征向量α1,α2, …,αd, 将变换矩阵记为ADLNPE=(α1,α2, …,αd); 3.1 实验环境与实验数据 所有实验均在CPU为Pentium(R)Dual-CoreE5300, 内存为2GB环境下, 用MATLAB2010b实现. 实验数据来自于warpPIE10P、colon、lymphoma、Coffee、BreastCancerWisconsin(Diagnostic)(wdbc)和Ringnorm(ring). 其中,warpPIE10P是图像数据集, 包含10个人在不同光线下各种表情的图像;colon和lymphoma是基因数据,Coffee是时间序列数据. 数据描述详见表1. 表1 实验数据简介 3.2 实验结果与分析 为验证DLNPE算法的有效性, 将其与NPE[6]、 NPDE[7]、 LPP[9]、 DLPP[10]4种方法进行对比. 其中NPE、 LPP是无监督降维方法, NPDE、 DLPP是有监督降维方法. 用这5种方法对上述6个数据进行降维, 在相同维度下用SVM方法进行分类. 最后以各维度上分类精度高低作为评价降维算法有效性的标准. 实验对比的5种算法涉及近邻参数k, 均设置在[1, 10]之间. SVM的核函数采用多项式核函数, 核函数参数设置为1. 实验结果如图1所示: 由图1可知, 有监督降维方法DLNPE、 NPDE、 DLPP总体上优于无监督降维方法LPP、 NPE; 在有监督方法中, 用DLNPE算法降维后的分类精度和稳定性上都优于NPDE和DLPP算法. 以图1(f)ring数据为例, DLNPE+SVM、 NPDE+SVM、 DLPP+SVM分类精度和LPP+SVM、 NPE+SVM相比都较优; 在有监督方法中, DLNPE+SVM算法的分类精度基本上处于NPDE+SVM、 DLPP+SVM算法上方并最终趋于稳定状态. 而对于图1(b)colon数据, 当维数降至22时, 部分特征之间的相关系数最高可达0.936 4. 特征之间冗余性很大, 造成DLNPE+SVM算法精度突然下降. 但这不影响算法的整体效果. 通过以上实验充分说明DLNPE算法是有效可行的. 图1 六个数据上的实验结果 为了提高NPE的性能, 本文通过引入有效的判别信息, 提出判别局部近邻保持嵌入算法(DLNPE). 该算法能够反映局部结构中邻域样本的不同类差异. 通过优化目标函数, 使得嵌入低维空间的数据类内保持固有的邻域结构, 且不同类别间的距离最大化, 从而获得具有鉴别力的投影矩阵. 实验结果也表明DLNPE算法与现有四种降维方法比较, 可以获得较高的分类精度. [1] Jolliffe I. Principal component analysis[M]. [s.l.]: John Wiley & Sons, 2005. [2] 边肇祺, 张学工. 模式识别[M]. 2版. 北京: 清华大学出版社, 2000. [3] Tenenbaum J B, De S V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5 500): 2 319-2 323. [4] Belkin M, Niyogi P. Laplacian eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1 373-1 396. [5] Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5 500): 2 323-2 326. [6] He Xiaofei, Cai Deng, Yan Shuicheng,etal. Neighborhood preserving embedding[C]//Proceeding of the Tenth IEEE International Conference on Computer Vision. Washington D C: IEEE, 2005: 1 208-1 213. [7] 王国强, 欧宗瑛, 刘典婷, 等. 基于保持近邻判别嵌入的人脸识别[J]. 大连理工大学学报, 2008, 48(3): 378-382. [8] Sugiyama M, Idé T, Nakajima S,etal. Semi-supervised local fisher discriminant analysis for dimensionality reduction[J]. Machine Learning, 2010, 78 (1/2): 35-61. [9] He Xiaofei, Niyogi P. Locality preserving projections[C]//Advance in Neural Information Processing Systems. Vancouver: MIT Press, 2003: 153-162. [10] Yu Weiwei, Teng Xiaolong, Liu Chongqing. Face recognition using discriminant locality preserving projections[J]. Image and Vision Computing, 2006, 24(3): 239-248. (责任编辑: 林晓) Dimensionality reduction of neighborhood preserving embedding based on discrimination information ZHANG Haiwu, CHEN Xiaoyun (College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China) Because traditional neighborhood preserving embedding (NPE) focuses on keeping a sample of local structure without taking category information into account, the discriminant local neighborhood preserving embedding algorithm is proposed. The algorithm use the local structure of samples points to construct the new definition within-class and between-class scatter matrix, which are introduced into the objective function as the discrimination information. The experimental results on six real data show that the algorithm is effective. dimensionality reduction; neighborhood preserving embedding; discrimination information; local structure 10.7631/issn.1000-2243.2015.04.0466 1000-2243(2015)04-0466-05 2014-03-13 陈晓云(1970-), 教授, 主要从事数据挖掘、 模式识别、 机器学习等方面研究, c_xiaoyun@21cn.com 福建省新世纪优秀人才基金资助项目(XSJRC2007-11) TP311 A
2 判别局部近邻保持嵌入(DLNPE)
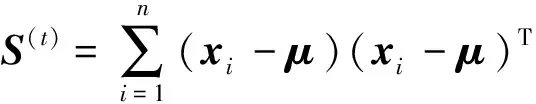
3 实验






4 结论

