评Freundlich吸附等温式的推导

史济斌　刘国杰

(华东理工大学化学系　上海 200237)

评Freundlich吸附等温式的推导

史济斌刘国杰

(华东理工大学化学系上海 200237)

摘要叙述了Freundlich吸附等温式的几种主要的推导方法，以及这些推导所反映的物理模型，并对它们进行了评价。

关键词气-固吸附Freundlich吸附等温式吸附的物理模型

The Derivation of Freundlich Adsorption Isotherm

Shi JibinLiu Guojie

(DepartmentofChemistry,EastChinaUniversityofScienceandTechnology,Shanghai200237,China)

AbstractThis paper introduces a few major methods and the associated physical models for deriving the Freundlich isotherm. Review comments are made to provide recommendation for physical chemistry teaching.

Key WordsGas-solid adsorption; Freundlich isotherm; Physical models for adsorption

Freundlich吸附等温式

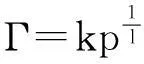
(1)

是表面吸附的一个重要公式。它不仅适用于气体在固体表面上的吸附，而且也适用于溶液中溶质在固体表面上的吸附。它的广泛适用性和公式的简单形式，使它具有很高的实用价值。因此，在国内外物理化学教材中无不提及这个吸附等温式。

然而，与其他吸附等温式不同，它最初是一个纯经验公式，出现于1895年，由Boedecker首先提出，后因Freundlich的大力推荐和推广使用而得名[1]。一个经验规律获得了广泛的应用，其中必有科学的渊源，故引起了大家的关注。1930年，Rideal用热力学方法导得了这个等温式。时隔4年，前苏联学者Zeldowitsch也从不同的角度导出了这个等温式，但推导不够好。1947年，两位美国学者Halsey和Taylor在研究氢气在钨粉上的吸附时，才明确地提出了这个吸附等温式的理论模型。下面便来讨论它的几种主要推导方法，以及推导所反映的物理模型，并对它们作出评价和推荐。

1Rideal推导[2]

Rideal认为，这个吸附等温式可通过引入适当的界面状态方程由Gibbs吸附等温式导得。众所周知，Gibbs吸附等温式是由界面系统的热力学基本方程结合Gibbs界面相模型得到，它原则上可适用于任何界面吸附，其中也包括气固吸附。若气相压力不高，该等温式可表示成：

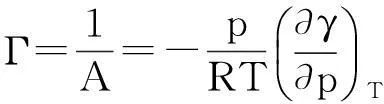
(2)

式(2)亦称Gibbs吸附公式。式中p为吸附质的平衡压力，A为1mol吸附质所占的界面面积，1/A即为吸附量Γ。

当吸附为单分子层时，已吸附的气体可用一个二维状态方程描述。若吸附气体可视为理想气体，则二维状态方程为：

πA=RT

(3)

式中π=γ0-γ，称为表面压或铺展压，其值为吸附前后界面张力之差。

倘若被吸附的气体分子间是有相互作用的，则式(3)应修正为:

πA=lRT

(4)

若修正因子l<1，表示吸附层中气体分子间为吸引力；若l>1，则为排斥力。将式(4)中的π对A求导，可得：

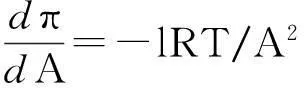
(5)

由于dπ=-dγ，则：

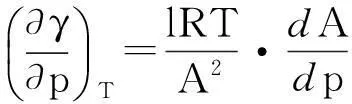
(6)

将式(6)代入式(2)，可得:

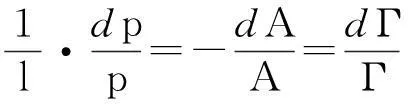
(7)

这是因为Γ=1/A，dΓ=-dA/A2。积分式(7)，则有：

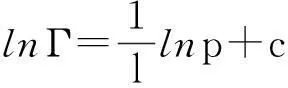
(8)

令积分常数c=lnk，得：

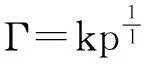
这就是式(1)。由于大量吸附表明参数l>1，故吸附层中分子间存在排斥力。

Rideal的上述推导表明，Freundlich吸附等温式是Gibbs吸附公式的一个特例。它将被吸附分子看成单分子层的二维离域气体，它们的分子间存在着排斥作用，这就是推导得到的结论。

2Halsey-Taylor推导[3-4]

这种推导是以Langmuir吸附模型为基础的。众所周知，Langmuir吸附等温式

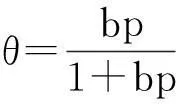
(9)

是建立在如下吸附模型之上的:① 固体表面的吸附活性是均一的;② 每一个吸附中心只吸附一个气体分子;③ 被吸附的气体分子是定域的,且相互间没有作用力。可见，这是一个理想的吸附模型，实际上是难以满足的。

在Langmuir的原始推导中，吸附系数b被令为常数。统计力学推导表明[5]:

(10)

意即吸附焓ΔadsHm不随覆盖度而改变，模型的第①点就体现于此。

Halsey和Taylor试图修正这一点。他们认为固体表面的吸附活性应是不均一的，不同吸附中心对气体的吸附强弱应不相同，吸附强者吸附热大，吸附弱者吸附热小，故b值不应是常数，而应随θ而变。他们按b值的大小，将固体表面划分成许多区域，令每一个区域有相同的b值。于是，每个区域应服从Langmuir吸附等温式:

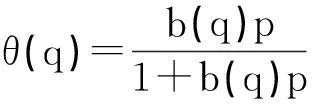
(11)

式中q=-ΔadsHm，为摩尔吸附焓的负值，称为吸附热。故总的表面覆盖度为：

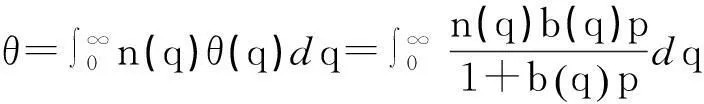
(12)

式中n(q)为吸附热在q→q+dq区间的吸附中心在总吸附中心中所占的分数。

Halsey和Taylor的一个重要假设是，函数n(q)是连续的，且可用下式描述:

n(q)=n0exp(-q/qm)

(13)

式中n0和qm是两个特性常数。式(13)意即固体表面上吸附中心的分布是按活性增高而呈指数减少。将式(10)和式(13)代入式(12)，便得:

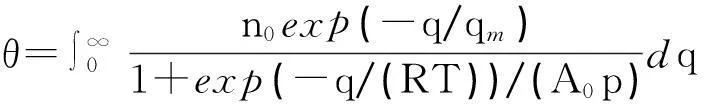
(14)

式(14)在q≫πRT时是可积分的，所得结果为:

θ=(A0p)RT/qm·n0qm

(15)

将式(15)等号两边取对数，得:

RTln(A0p)=qmlnθ-qmln(n0qm)

(16)

再在保持θ不变的条件下对温度求偏导，则有：

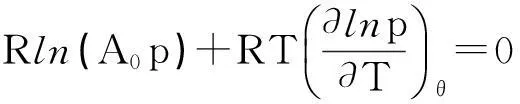
(17)

q=-qmlnθ+qmln(n0qm)

(18)

式(15)和式(18)即Halsey和Taylor所得结果。由这两个式子不难看出，当p=1/A0时，θ=n0qm，此时q=0；而当p>1/A0时，θ>n0qm，此时q<0。然而，热力学认为，吸附应当是放热的，故p>1/A0是不符合热力学要求的。这就意味着p=1/A0是饱和的平衡压力，相应的覆盖度应是n0qm=1。于是，由式(15)不难得到：

θ=(A0p)RT/qm

(19)

此外，因n0qm=1，由式(18)还可得到:

q=-qmlnθ

(20)

它意味着吸附热随覆盖度的增大而指数减小。

上述推导说明了Freundlich吸附等温式对应了这样一个模型：① 固体表面的吸附活性是不均一的；② 吸附是单分子层的；③ 被吸附气体分子是定域的，且彼此之间没有作用力。显然，这与Rideal得到的结论大相径庭。因此，Adamson[6]认为，即使实验数据与式(19)相符，也不能作为表面不均一的证明，而只能说表面像是不均一的。

其实，Rideal的推导用的是一种宏观的热力学方法，他将Gibbs吸附公式与一个二维状态方程相结合，而这个状态方程是由二维理想气体状态方程乘上一个修正因子l构成。由于

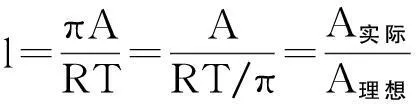
(21)

可将其视为二维气体的压缩因子。倘若l>1，气体分子间的作用力便是排斥力。这种热力学方法的实质是将固体表面对气体的吸附作用等效于二维气体分子间的排斥力，它并不涉及吸附的真实微观图像，故Rideal的推导结果是不能作为吸附模型依据的。

本文认为，Halsey-Taylor推导所建立的吸附模型是可信的，但推导过于复杂，不适合在普通物理化学教材中采用。因此，本文推荐如下第3种方法，它实为Halsey-Taylor推导的简化。

3第3种推导[1]

由Halsey-Taylor建立的吸附模型可见，它与Langmuir吸附模型的区别仅在于固体表面是不均一的，亦即表面吸附中心的活性是有区别的。这种区别在于不同的吸附中心吸附放出的热是不相同的，因此，表征活性的吸附系数b应是吸附热q的函数，即：

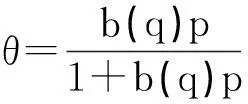
(22)

式中b(q)如式(10)所示，为:

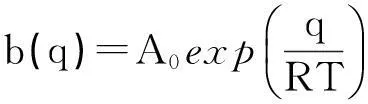
将它代入式(22)，可得：

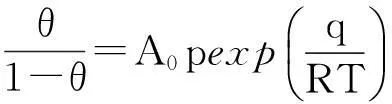
(23)

若假定q与θ的关系如式(20)所示，将它代入式(23)，并在等号两边取对数，则得：

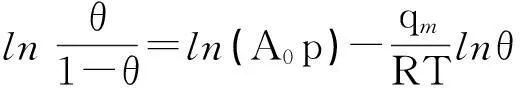
(24)

在θ接近0.5的中等覆盖度情况下，因为等号左边是个很小的值，式(24)可近似地表示为：

θ=(A0p)RT/qm

这个式子即为式(19)，亦即Freundlich吸附等温式。

这种推导方法实际上是将Halsey-Taylor推导所得的式(20)作为假定，从而使Freundlich吸附等温式的导出大为简化；它不仅物理意义清晰，而且还阐明了这个吸附等温式只能适用于中等吸附程度；同时，它也说明了在如此吸附程度下，被吸附分子间不太可能出现排斥力占据主导作用的情况。因此，这种推导方法很适合用于普通物理化学教材。

参考文献

[1]章燕豪.吸附作用.上海:上海科学技术文献出版社,1989

[2]Rideal E K.Surface Chemistry.Cambridge:Cambridge Univ Press,1930

[3]Halsey G,Taylor H S.JChemPhys,1947,15:624

[4]Trapnell B M W.Chemisorption.London:Butterworths,1955

[5]刘国杰,黑恩成.物理化学释疑.北京:科学出版社,2010

[6]Adamson A W.表面的物理化学(下册).第3版.顾惕人译.北京:科学出版社,1986

中图分类号O6；G64

doi:10.3866/pku.DXHX20150376