海表面温度的变分同化预报模式:初始场的全局优化
高艳秋,苏 洁,李 磊,吕咸青
(1.卫星海洋环境动力学国家重点实验室,浙江 杭州 310012;2.国家海洋局 第二海洋研究所,浙江 杭州310012;3.中国海洋大学 海洋环境学院 物理海洋学教育部重点实验室,山东 青岛 266100)
海表面温度的变分同化预报模式:初始场的全局优化
高艳秋1,2,苏 洁3,李 磊3,吕咸青3
(1.卫星海洋环境动力学国家重点实验室,浙江 杭州 310012;2.国家海洋局 第二海洋研究所,浙江 杭州310012;3.中国海洋大学 海洋环境学院 物理海洋学教育部重点实验室,山东 青岛 266100)
利用变分同化技术,将船舶报资料与海表面温度短期数值预报模式有机结合,实现了渤、黄、东海的海表面温度短期数值预报。本预报模式利用伴随方法实现了预报模式的全局优化,不但最大限度地利用了船舶报资料,而且初始温度场的调整由自动的数值迭代过程来实现。在渤、黄、东海海域,4个季节的典型月份的SST连续1个月的24 h后报结果与船舶报资料均方差均降至0.8 ℃以下。同化后海表面温度初始场的绝均差较同化前有显著下降。与以前所用的客观分析方法比较的结果表明,伴随同化的预报精度明显高于客观分析方法。
伴随同化;海表面温度;短期数值预报;渤、黄、东海
0 引言
海表面温度(Sea Surface Temperature,SST)作为海洋的重要因素之一,不仅影响海洋渔业资源的开发和利用,在海洋生态中具有重要的作用,而且它可以通过海-气相互作用,进而制约中长期数值天气预报的预报时效。SST预报的重要性是不言而喻的,许多学者曾对中国近海SST的数值预报进行过研究[1-4]。
由于计算机技术的飞速发展,SST数值预报模式的分辨率不断提高,预报精度也逐步提高[5-6]。随着模式误差的不断减小,初值质量的提高就显得越来越重要,并在海洋业务数值预报中受到越来越多的关注。因此,寻找一种有效的形成高质量初值的方法成为了海洋数值预报的一个关键步骤。
以往的客观分析方法实际上并未将观测资料与模型相拟合以实现对初始场的优化,因此很难通过观测资料构造出一个可以信赖的初始场。而没有合理的初始场,也就难以保证业务化预报的有效性。80年代发展起来的变分同化方法[7-8]以及变分同化技术的应用[9-11],为解决此问题奠定了坚实的基础。特别是近些年四维变分同化技术在海洋预报中的应用[5-6,12-14],为此问题的解决开辟了广阔的前景。
本文所采用的SST数值预报模式是由王赐震等[1-2]建立,后经过多位学者[15-18]加以改进后发展的海表面短期温度数值预报模式。特别是近些年,一些学者将该数值预报模式发展为变分同化模式。张建华 等[19]建立了一个有限域的SST短期动力数值二维预报模式,开创了第一代SST短期数值预报模式,利用伴随方法优化初始场,实效为3 d的预报精度均方误差达到1.0 ℃左右。朱江 等[20]将自适应同化方法应用到实际的SST资料同化中,结果表明该方法对海表和海面以下混合层的海温都能够进行较好的订正。马继瑞 等[21]利用变分伴随同化技术给出了中国近海SST数值预报同化模型5 d的试报结果,与观测值比较,整个区域的绝均差由同化前的2.71 ℃降至0.87 ℃。黄思训 等[22]以一维海温模式为例,采用变分资料同化技术及处理数学物理反问题的技巧对初始条件、边界条件和模式参数等进行了最优估计和确定。何忠杰 等[23]基于多重网格三维变分同化方法,研究了同化卫星测高和卫星遥感海面温度观测资料对中国海及邻近海域海面高与三维温盐流数值预报模型预报能力的影响。其中伴随同化方法具有很强的模式初始条件、边界条件和控制参数优化能力。伴随模式的主要特点体现在两个方面:一个是在预报的过程中实现了初始温度场全局优化的自动化,即预报过程中海表温度初始场的优化不需要预报员的直接参与,另一个是最大限度地利用了当前的船舶报资料,将可观测到的船舶报资料同化到数值预报模式中,实现了数值预报模式和观测资料的有机结合。
本文进一步发展了海表面短期数值预报模式,利用伴随同化方法,实现了海表面温度初始场的全局优化,进而进行SST的短期预报。
1 数值预报模式
本文所使用的SST数值预报模式是根据王赐震等[1-2]建立的SST数值预报模式发展而来的。模式的预报方程和初始边界条件,预报模式的参数以及改进如下所示。
1.1 模式预报方程组
连续方程:
(1)
动力学方程:
(2)
(3)
状态方程:
ρd=f(T,S)-ρc
(4)
热力学方程:
(5)
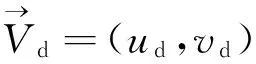
需要指出的是:在(1)~(4)式中,混合层深度h不随时间变化,而在(5)式中,h是随时间变化的,在模式中混合层深度的变化由大风引起的上混合层底部的夹卷和在浅水条件下由底摩擦引起的潮混合给出,见下式:
(6)
以上(1)~(6)式,加之初始条件和边界条件,构成近海异常海温数值预报模式闭合方程组。其中,根据王赐震 等[1-2]的表述,方程(1)~(4)和方程(5)中扣除海表面加热项和混合夹卷项构成模式的动力学部分,方程(5)中剩下的称为物理学部分。
1.2 模式的初始条件和边界条件
初始条件:SST的初值由旬平均的常规SST船舶报资料给出。
岸边界条件:流速的法向分量为0,切向分量与内部流连续;温度取无热传导条件。
开边界条件:漂流由区域内的漂流沿流线方向外延给出;温度边界条件取辐射条件的一种,即流入定常,流出无梯度。
模式气象强迫场采用国家海洋局海洋环境预报中心中尺度数值预报模式MM5的预报结果[24]。海洋环境预报中心从2002年开始建立有限区域海面风场数值预报业务化系统,提供10°N~45°N、105°E~155°E海域内0.5°×0.5°网格点上的温、压、湿和风的逐时72 h预报。系统采用美国国家环境预报中心(NCEP)的初始分析场作为初估场,侧边界与美国全球预报系统(GFS)的预报嵌套采用松弛边界条件,积云对流参数化选用Grell方案[25],边界层参数化方案采用高分辨率行星边界层方案。该系统已于2003年8月开始在工作站上运行进行实时预报。
1.3 模式参数及模式改进
模式参数的确定见文献[18]。基于王赐震等人的工作[1-2,15-16],SST数值预报模式的改进包括两个方面:
(1) 模式结构的改进:a)建立‘.h’头文件,避免各子程序间的变量串用;b)加入地形资料和基本参量准备子程序,方便用户使用;c)对数组进行统一的定义,适于不同海区的应用;d)简化数据读写程序。
(2) 模式物理改进:a)在原模式中混合层深在动力部分为平底,在改进的模式中混合层深变为具有空间变化的形式;b)海水密度由常数变为空间变化的形式;c)气压由常数变为空间变化的形式;d)太阳辐射由月平均变为日(或小时)平均,程序中设置了开关,用户可根据预报要求选择日平均或小时平均太阳辐射;e)减小了温度方程的物理学部分的时间步长,原模式中温度方程的物理学部分计算时间步长为1 h,为了对物理学部分和动力部分引起的温度变化同时进行同化处理,将热力计算模块的计算时间步长调整为和动力计算相同的步长(180 s);f)进一步确定模式水深和混合层深临界值;g)考虑了风浪对海面反照率的影响,令海面反照率r与风速分段线性相关;h)对潮混合的处理,认为潮混合效应不改变温度,只改变混合层深度。
2 伴随模式
2.1 伴随方程及其推导
在本预报模式中,基于伴随同化方法,利用船舶报的温度资料,通过优化SST的初始场,来实现SST实效为3 d的预报。
代价函数衡量了模拟结果与实测数据的差异,对模拟效果具有较强的表征能力。描述SST预报和观测差值的代价函数定义为:
(7)
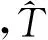
为了得到伴随方程以及初始场的校正关系式,构造Lagrange函数:
(8)
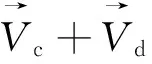
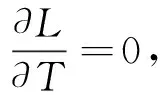
(9)
当然,根据离散化的热力学方程,
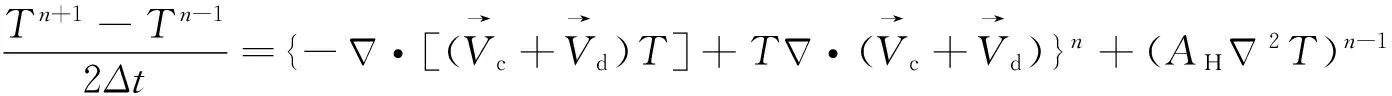
(10)
经过推导,可得到关于控制变量的梯度表达式:
(11)
控制变量的调整通过以下公式实现:
(12)
式中:β为步长因子。
2.2 伴随同化的实现步骤及实验设计
数值预报模式采用有限差分离散[27],即根据方程(10)~(12)实现伴随,具体步骤为:
(1) 给温度初始场赋值(参照旬平均的船舶报资料)。
(2) 积分正向过程。
(3) 判断后报结果与观测结果的均方差是否满足要求,如果满足,进入步骤(8);如果不满足要求,进入步骤(4)。
(4) 反向积分伴随方程,根据公式(10)计算。
(5) 根据表达式(11)计算代价函数关于初始温度场的梯度。
(6) 根据公式(12)校正温度初始场。
(7) 返回步骤(1)。利用改进后的控制变量开始下一次校正。
(8) 结束对初始温度场的校正,通过计算给出预报结果。
计算区域为24°N~40.75°N,117.25°E~130.75°E;空间分辨率为0.25°×0.25°。动力模式、物理模式与热力方程的积分时间步长都是180s。对2002年4个季度的代表月份(2月、5月、8月和11月)作连续1个月的预报。
3 数值实验与结果分析
在实际预报中,每天能够得到实时船舶报资料。这些珍贵的船舶报资料被认为是准确的,用来矫正预报程序使用的初始场。
3.1 伴随同化方法和客观分析方法的预报过程
为了与以前所用的客观分析方法进行比较,伴随同化和客观分析方法都有一个5d的起报过程,并且只利用预报前24h的船舶报资料得到预报使用的初始场,然后结合预报的气象强迫场进行72h的预报。使用同样的预报程序和同样的船舶报资料检验。以2月份为例分别说明客观分析方法和伴随同化的预报过程。
3.1.1 客观分析方法的预报步骤
本次实验中,客观分析方法的预报步骤如下(其中,步骤(1)和(2)为起报过程):
(1) 用2002年1月26日0时(世界时)的背景场(即下旬旬平均的船舶报SST场)作为客观分析方法的基本场,结合25日0时至25日24时时间段的船舶报资料,可以得到26日0时的预报程序用的初始SST场。代入预报程序,可以得到27日、28日和29日0时的预报SST场。
(2) 用27日0时的预报SST场作为客观分析方法的基本场,结合26日0时至26日24时时间段的船舶报资料,可以得到27日0时的预报程序用的初始SST场。代入预报程序,可以得到28日、29日和30日0时的预报SST场。
(3) 仿照步骤(2),直到得到31日0时的预报程序用的初始SST场。代入预报程序,可以得到2月1日、2日和3日0时的预报SST场。至此为止,完成了起报之后第1天的预报。
(4) 之后,顺次作出第2天、第3天,…的预报。直到下一次重新起报。
3.1.2 伴随同化的预报步骤
本次实验中,伴随同化的预报步骤如下(其中,步骤(1)~(3)为起报过程):
(1) 用2002年1月26日0时(世界时)的背景场(即下旬旬平均的船舶报SST场)作为同化程序的初始场,同化26日0时至26日24时时间段的船舶报资料,可以得到27日0时的同化SST场。
(2) 将27日0时的同化SST场作为同化程序的初始场,同化27日0时至27日24时时间段的船舶报资料,可以得到28日0时的同化SST场。
(3) 仿照步骤(2),直到得到31日0时的同化SST场。
(4) 将31日0时的同化SST场作为预报程序的初始场,代入预报程序,可以得到2月1日、2日和3日0时的预报SST场。至此,完成了起报之后第1天的预报。
(5) 仿照步骤(2),将31日0时的同化SST场作为同化程序的初始场,同化31日0时至24时时间段的船舶报资料,得到2月1日0时的同化SST场;仿照步骤(4),将1日0时的同化SST场作为预报程序的初始场,代入预报程序,可以得到2日、3日和4日0时的预报SST场。这是起报之后第2天的预报。
(6) 之后,顺次作出起报之后第3天、第4天,…的预报。
如果观测资料足够多,从理论上讲这样可以连续将预报一直做下去。然而由于预报一段时间之后误差累计比较大,所以连续预报一段时间以后必须用新的旬平均场重新起报一次。所谓重新起报,就是对新的时间序列再重复步骤(1)~(6)。
3.2 伴随同化方法的结果
以2月份为例,15日船舶报的位置如图1所示,需要指出的是,一些位置在不同时间有重复观测。15日同化前和同化后的SST初始场如图2所示。
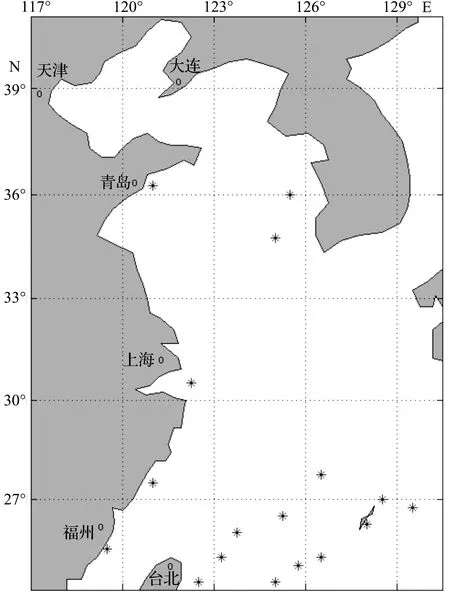
图1 2002年2月15日船舶报观测站位分布
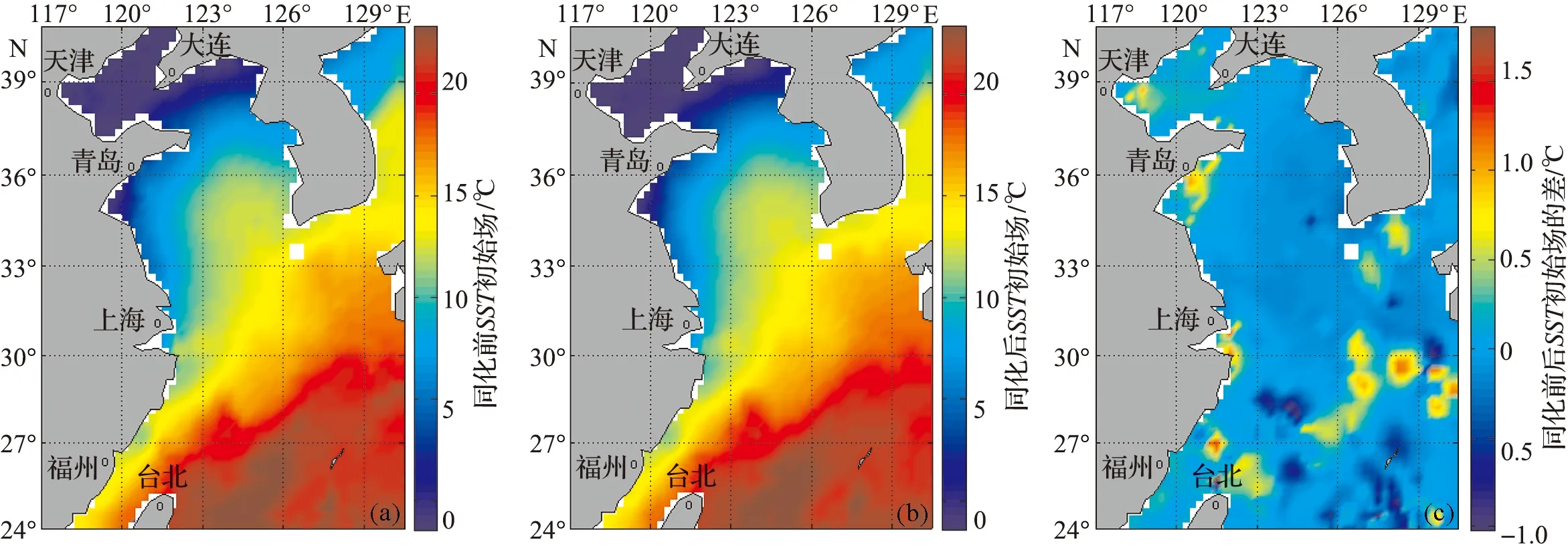
图2 2002年2月15日同化前的SST初始场(a)和同化后的SST初始场(b)以及同化前与同化后初始场的差(c)
利用改进的预报模型,在渤、黄、东海海域,针对4个季节的典型月份连续1个月的24h后报结果与船舶报资料均方差均降至0.8 ℃以下。4个月份同化前后SST初始场的绝均差如表1所示。同化后SST初始场的绝均差较同化前SST初始场的绝均差最多下降了61.84%,最少下降了48.41%,表明了使用伴随同化方法,渤、黄、东海的SST预报取得成功。
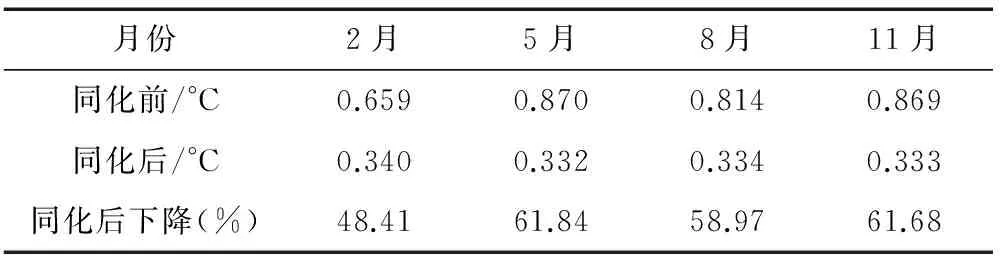
表1 同化前后渤、黄、东海SST初始场的绝均差
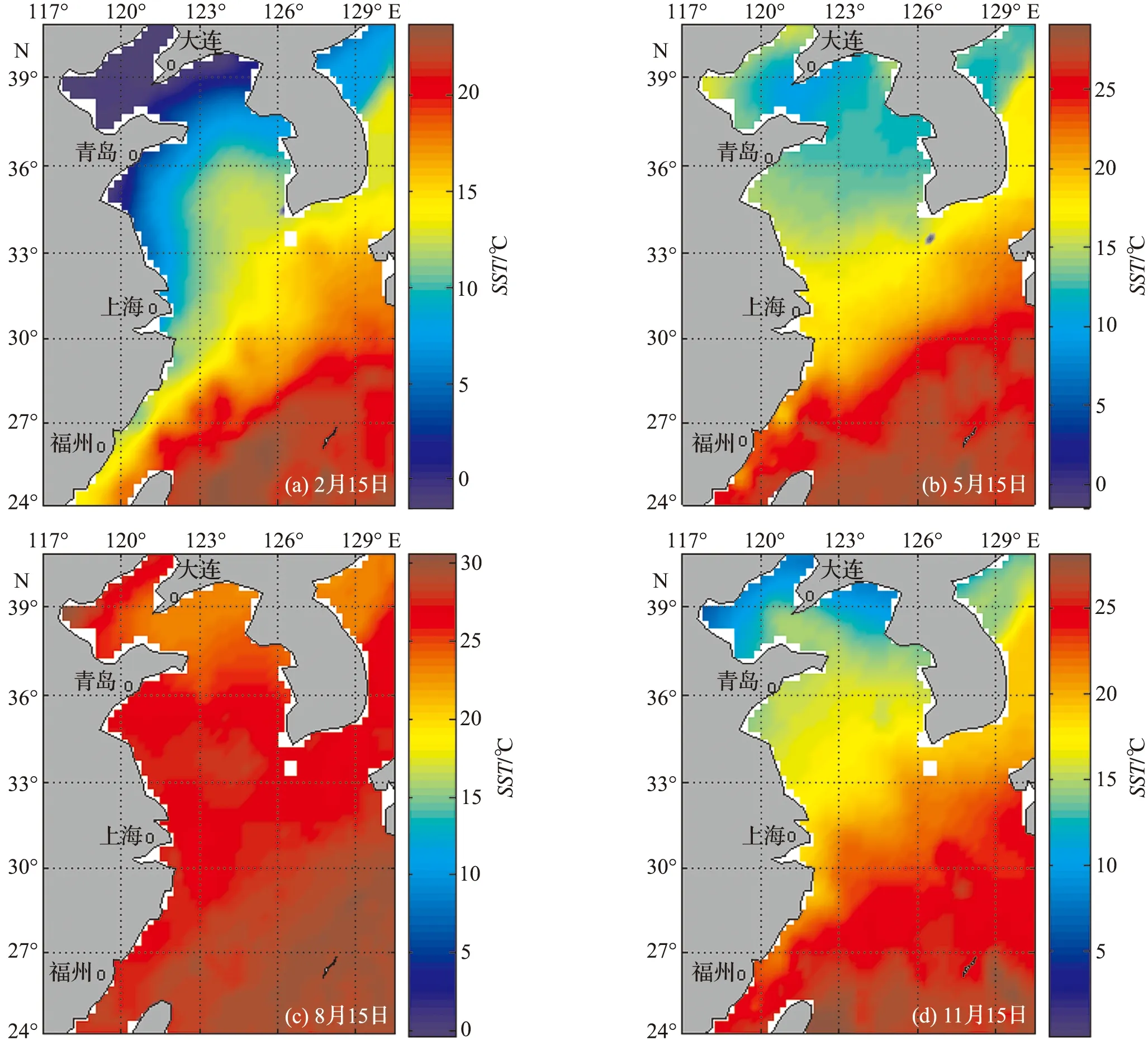
图3 使用伴随同化方法预报SST的结果
4个月份中15日的SST预报结果如图3所示,其它日期的预报结果类似,不再展示。在2月份和11月份的15日,整个渤、黄、东海海域从北向南,SST逐渐升高:其中2月份,渤海北部的SST可低至0 ℃,台湾岛东部的SST可达24 ℃;11月份,渤海湾最低温度低至6 ℃,台湾岛东部可达28 ℃。在5月份和8月份的15日,整个渤、黄、东海海域的SST差异变小;渤海沿岸海区比外海SST高;在黄海和东海海域自北向南SST逐渐升高。图3的结果表明,使用伴随同化方法在物理上是合理的。
3.3 伴随同化方法与客观分析方法的比较
本实验中,将数值模拟预报的结果与船舶报资料的均方差作为检验预报效果的标准。4个季度的代表月份连续1个月的预报结果与船舶报资料的均方差如图4所示。与以前所用的客观分析方法比较的结果表明,除8月份外,伴随同化的预报精度明显高于以前所用的客观分析方法。笔者猜测,8月份SST在南北方向上的梯度较小,整体温度较高,此时的预报结果对初始SST的敏感性较小。
表2为4个季度的代表月份预报结果与船舶报资料的均方差的平均值。使用伴随同化方法,均方差的平均值较客观分析方法至少下降了11.40%,进一步表明使用伴随同化方法较客观分析方法可以提高预报精度。
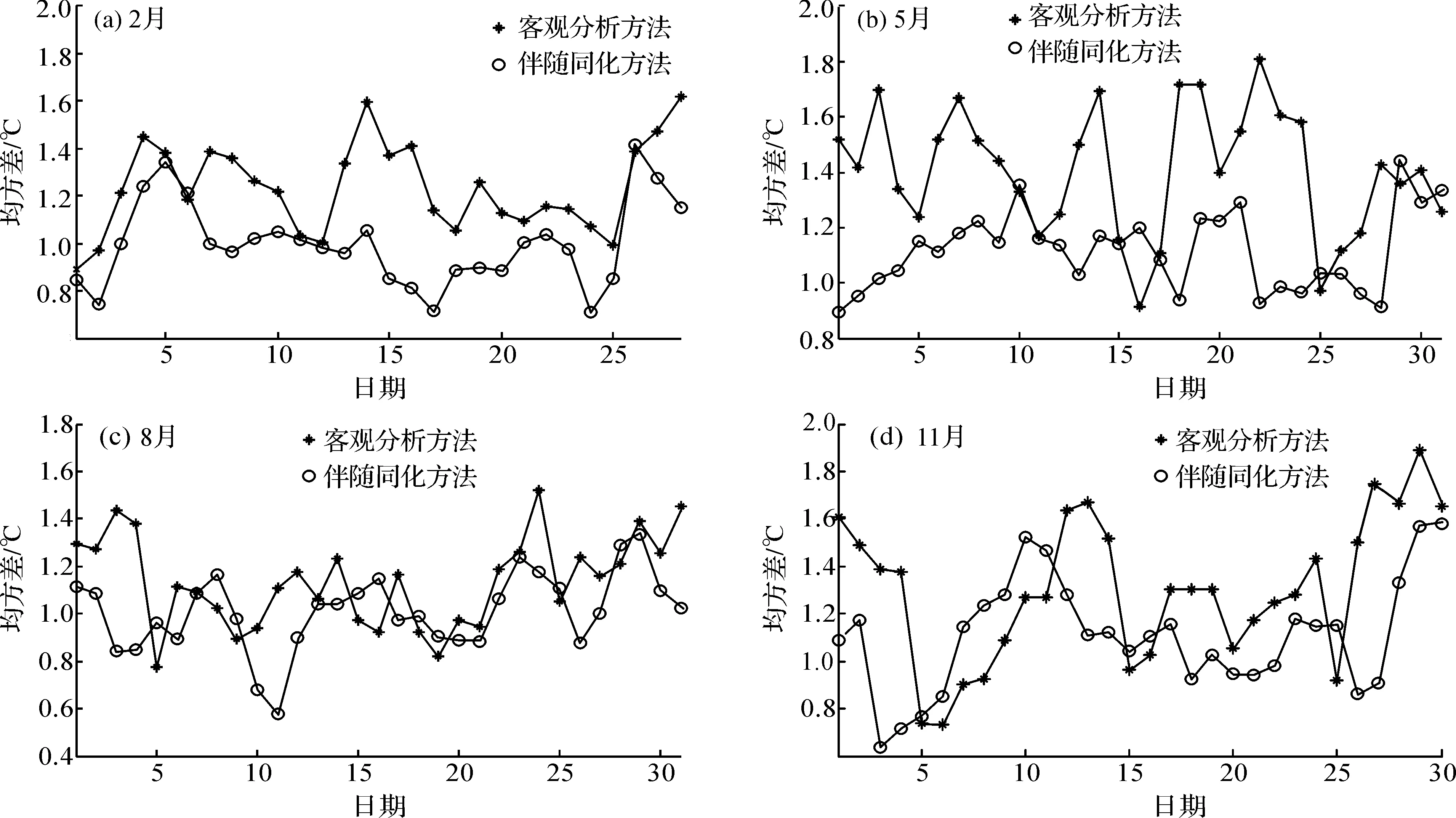
图4 伴随同化方法和客观分析方法的SST预报均方差
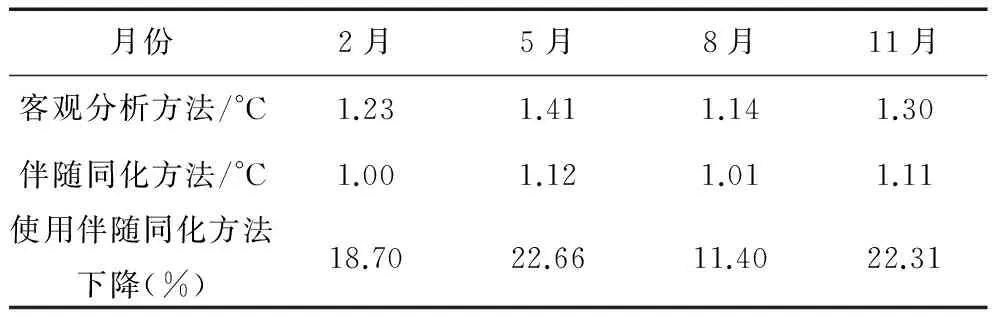
表2 4个季度的代表月份预报结果与船舶 报资料的均方差的平均值
4 结论
本文利用变分同化技术,改进了之前的SST数值预报模式,将船舶报资料与海表面温度短期数值预报模式有机结合,实现了渤、黄、东海的海表面温度短期数值预报。
本次实验在整个渤、黄、东海海域,针对2002年4个季度的代表月份(2月、5月、8月和11月)的SST连续1个月的24 h后报结果与船舶报资料均方差均降至0.8 ℃以下。与以前所用的客观分析方法的比较结果表明,伴随同化的预报精度明显高于客观分析方法。同化后SST的绝均差较同化前SST的绝均差有显著下降。使用伴随同化方法,预报结果与船舶报资料的均方差的平均值较客观分析方法有所下降。
本预报模式利用伴随方法,通过代价函数关于初始温度场的梯度校正初始温度场,直到后报结果与观测结果的均方差满足要求,实现了预报模式的全局优化,不但最大限度地利用了船舶报资料,而且初始温度场的调整由自动的数值迭代过程来实现,不再需要预报员的直接参与。
[1] WANG Ci-zhen, SU Yu-song. A model of SST prediction for limited region, I. The dynamical equations[J]. Oceanologia et Limnologia Sinica,1990,21(9):418-424. 王赐震,苏育蒿.一种有限区域海表面温度预报模式,I.动力学部分[J].海洋与湖沼,1990,21(9):418-424.
[2] WANG Ci-zhen, SU Yu-song. A model of SST prediction for limited region, Ⅱ. The model’s physical equations [J]. Oceanologia et Limnologia Sinica,1991,22(1):69-77. 王赐震,苏育蒿.一种有限区域海表面温度预报模式,II.物理学部分[J].海洋与湖沼,1991,22(1):69-77.
[3] WALLCRAFT A J, KARA A B, HURLBURT H E, et al. Value of bulk heat flux parameterizations for ocean SST prediction [J].Journal of Marine Systems,2008,74(1):241-258.
[4] ZHANG W G, WILKIN J L, ARANGO H G. Towards an integrated observation and modeling system in the New York Bight using variational methods. Part I: 4DVAR data assimilation [J]. Ocean Modelling,2010,35(3):119-133.
[5] PENG Shi-qiu,XIE Lian. Effect of determining initial conditions by four-dimensional variational data assimilation on storm surge forecasting[J]. Ocean Modelling,2006,14(1):1-18.
[6] PENG Shi-qiu, XIE Lian,PIETRAFESA L J. Correcting the errors in the initial conditions and wind stress in storm surge simulation using an adjoint optimal technique[J]. Ocean Modelling,2007,18(3):175-193.
[7] ANDERSON D L T, SHEINBAUM J, HAINES K. Data assimilation in ocean models[J]. Reports on Progress in Physics,1996,59(10):1 209-1 266.
[8] NAVON I M. Practical and theoretical aspects of adjoint parameter estimation and identifiability in meteorology and oceanography [J]. Dynamics of Atmospheres and Oceans,1997,27(1):55-79.
[9] ROQUET H, PLANTON S. Determination of ocean heat fluxes by a variational method [J]. Journal of Geophysical Research,1993,98(c6):10 211-10 221.
[10] YU Li-san, O'BRIEN J J. Variational data assimilation for determining the seasonal net surface heat fluxes using a ropical Pacific Ocean Model [J]. Journal of Physical Oceanography,1995,25(10):2 319-2 343.
[11] YUAN Dong-liang, HSUEH Y. Inverse determination of surface heat flux over the Yellow Sea in winter 1986 from sea surface temperature data [J]. Journal of Physical Oceanography,1998,28(5):984-990.
[12] POWEL B S, ARANGO H G, MOORE A M, et al. 4DVAR data assimilation in the Intra-Americas Sea with the Regional Ocean Modeling System (ROMS) [J]. Ocean Modelling,2008,23(3):130-145.
[13] POWELB S, MOORE A M, ARANGO H G, et al. Near real-time ocean circulation assimilation and prediction in the Intra-Americas Sea with ROMS[J]. Dynamics of Atmospheres and Oceans,2009,48(1):46-68.
[14] BROQUET G, EDWARDS C A, MOORE A M, et al. Application of 4D-Variational data assimilation to the California Current System[J]. Dynamics of Atmospheres and Oceans,2009,48(1):69-92.
[15] WANG Ci-zhen, LI Xu-hua, QI Jian-hua, et al. A numerical model for predicting offshore SST anomaly in the East China Sea, I. Establishment of model [J]. Acta Oceanologica Sinica,1998,20(3):27-34. 王赐震,李许花,戚建华,等.中国近海异常海温数值预报模式研究,I.模式的建立[J].海洋学报,1998,20(3):27-34.
[16] WANG Ci-zhen, LI Xu-hua, QI Jian-hua, et al. A numerical model for predicting offshore SST anomaly in the East China Sea, II. Factor analyses and experiment forecast [J]. Acta Oceanologica Sinica,1998,20(5):19-26. 王赐震,李许花,戚建华,等.中国近海异常海温数值预报模式研究,II.因子分析和试预报[J].海洋学报,1998,20(5):19-26.
[17] SU Jie, LI Lei, BAO Xian-wen, et al. Numerical experiment of SST response to typhoon process in Yellow Sea and Bohai Sea [J]. Journal of Ocean University of Qingdao,2001,31(2):165-172. 苏洁,李磊,鲍献文,等.黄、渤海表层海温对台风过程响应数值试验[J].青岛海洋大学学报,2001,31(2):165-172.
[18] SU Jie, LI Lei, GAO Guo-ping, et al. Numerical experiment of the summer SSTA affected by sub-tropical high in the Yellow Sea and Bohai Sea[J]. Journal of Ocean University of Qingdao,2000,30(4):567-574. 苏洁,李磊,高郭平,等.副高对黄渤海夏季异常海温影响的数值试验[J].青岛海洋大学学报,2000,30(4):567-574.
[19] ZHANG Jian-hua, SU Jie, LI Lei, et al. A numerical model for predicting shortdated SST in the China Sea [J]. Marine Forecasts,2005,22(Supplement):122-127. 张建华,苏洁,李磊,等.SST短期数值预报[J].海洋预报,2005,22(增刊):122-127.
[20] ZHU Jiang, WANG Hui, ZHOU Guang-qing. Adaption variational assimilation of SST[J]. Chinese Sciences Bulletin,2002,47(19):1 517-1 520. 朱江,王辉,周广庆.海表温度的自适应变分同化[J].科学通报,2002,47(19):1 517-1 520.
[21] MA Ji-rui, HAN Gui-jun, LI Dong. A study on the application of variational adjoint data assimilation for numerical prediction of sea surface temperature [J]. Acta Oceanologica Sinica,2002,24(5):1-7. 马继瑞,韩桂军,李冬.变分伴随数据同化在海表面温度预报中的应用研究[J].海洋学报.2002,24(5):1-7.
[22] HUANG Si-xun, HAN Wei, WU Rong-sheng. Theoretical analysis and numerical experiment of variational data assimilation in one-dimensional SST model combining inverase problem skill[J]. Science in China :Series D,2003,33(9):903-911. 黄思训,韩威,伍荣生.结合反问题技巧对一维海温模式变分资料同化的理论分析及数值实验[J].中国科学:D缉,2003,33(9):903-911.
[23] HE Zhong-jie, HAN Gui-jun, LI Wei, et al. Experiments on assimilation of satellite data in the China Seas and adjacent seas[J]. Journal of Ocean University of China,2010,4(9):1-7. 何忠杰,韩桂军,李威,等.中国海及邻近海域卫星观测资料同化实验[J].中国海洋大学学报,2010,4(9):1-7.
[24] LING Tie-jun, ZHANG Yun-fei, YANG Xue-lian, et al. The application of MM5 model to predict sea surface wind field [J]. Marine Forecasts,2004,21(4):1-9. 凌铁军,张蕴斐,杨学联,等.中尺度数值预报模式(MM5)在海面风场预报中的应用[J].海洋预报,2004,21(4):1-9.
[25] GRELL G A. Prognostic evaluation of assumptions used by cumulus parameterization [J]. Monthly Weather Review,1993,121(3):764-787.
[26] YU Li-san, O’BRIEN J J. On the initial condition parameter estimation [J]. Journal of Physical Oceanography,1992,22(11):1 361-1 364.
[27] SIRKES Z. Finite difference of adjoint or adjoint of finite difference [J]. Monthly Weather Review,1997,125(12):3 373-3 378.
Application of adjoint assimilation method in a sea surface temperature prediction model: global optimization of the initial field
GAO Yan-qiu1,2, SU Jie3, LI Lei3, LÜ Xian-qing3
(1.StateKeyLaboratoryofSatelliteOceanEnvironmentDynamics,SOA,Hangzhou310012,China;2.TheSecondInstituteofOceanography,SOA,Hangzhou310012,China;3.KeyLaboratoryofPhysicalOceanographyMOEChina,OceanUniversityofChina,Qingdao266100,China)
Adjoint assimilation technique, in conjunction with the ship reported data, was applied to a short term numerical prediction model in order to realize automatic short term SST forecast in the Bohai, the Yellow Sea and the East China Sea. The prediction model, using the adjoint assimilation method, achieved a global optimization of the initial SST field. It was not only making the best use of the ship reported data, but also the adjustment of the initial temperature field was realized by interaction automcticully. Corresponding to the four typical months (February, May, August and November) of four seasons respectively in 2002, the forecast was performed for a month continuously. The results indicate that the root mean square errors between the hindcasts of 24 successive hours and the ship reported data are reduced to below 0.8 ℃. The mean absolute errors in initial fields of SST are reduced markedly, compared with the values before assimilation. The forecast accuracy is improved with the adjoint assimilation method compared with the results from the objective analysis method.
adjoint assimilation method; sea surface temperature; short term numerical prediction; the Bohai, the Yellow Sea and the East China Sea
10.3969/j.issn.1001-909X.2015.01.001.
2014-09-18
2014-12-03
国家自然科学基金项目资助(41276029);国家“863“计划项目资助(2013AA122803);国家公益性行业(气象)科研专项项目资助(GYHY201306049)
高艳秋(1987-),女,山东临沂市人,助理研究员,主要从事物理海洋学方面的研究。E-mail:gaoyanqiujuly11th@163.com
P731.31
A
1001-909X(2015)01-0001-08
10.3969/j.issn.1001-909X.2015.01.001
高艳秋,苏洁,李磊,等.海表面温度的变分同化预报模式:初始场的全局优化[J].海洋学研究,2015,33(1):1-8,
GAO Yan-qiu, SU Jie, LI Lei,et al. Application of adjoint assimilation method in a sea surface temperature prediction model: global optimization of the initial field[J]. Journal of Marine Sciences,2015,33(1):1-8, doi:10.3969/j.issn.1001-909X.2015.01.001.

