基于CATIA二次开发中点误差控制算法实现及其应用

昌河飞机工业（集团）有限责任公司 吴献珍

山东理工大学 机械工程学院 徐汝锋

北京航空航天大学 机械工程及自动化学院 贺 英

上海安托信息技术有限公司 阚文军

目前，复杂曲面已经广泛应用于航空、航天、船舶和模具等行业，复杂曲面的高效高精度加工制造成为研究的热点。针对复杂曲面加工，目前我国很多企业仍采用球头刀行切的三轴数控加工工艺，该工艺的缺点是加工效率较低，且加工表面质量较差，需要后续大量的手工抛磨。国外企业早已采用了五轴数控加工工艺，这将大幅提高复杂曲面的加工效率和加工质量。与三轴数控机床相比，五轴数控机床由于增加了2个转动自由度，其刀具控制更加灵活，因此具有更多的加工优势。然而，其五轴数控加工编程方法更加复杂，在某种程度上也限制了五轴数控加工工艺的应用。因此，针对五轴数控编程算法，国内外学者开展了大量研究。

五轴数控加工编程算法根据刀具定位点的不同，可以分为以下3种：（1）基于单切触点的刀位优化算法，包括刀轴倾斜法[1]、曲率匹配算法[2-4]等；（2）基于双切触点的刀位优化算法，包括多点法[5-6]等；（3）基于端点或中点的刀位优化算法，包括端点误差控制算法[7]、中点误差控制算法[8-9]等。其中，中点误差控制算法是以“W”型误差曲线的中间点进行刀具定位，然后通过优化刀具的前倾角和侧偏角容易获得最大的加工带宽。

在直升机零件及模具实际制造中，涉及了大量开敞型复杂曲面结构，如钣金蒙皮件、机加曲面结构件、复合材料曲面构件及曲面模夹具等。目前，针对复杂曲面数控加工的实现方式主要有2类：固定轴加工和五轴加工。固定轴切削是依据球头刀刃大小不同实现行宽不等密集型刀路切削，一般刀轨行间距在0.5～2mm。该方式的优点是计算方法简单、计算速度快，缺点是加工效率低、刀具与加工曲面垂直切削时刀具磨损较快、加工表面质量较差。而目前CATIA软件中包含五轴曲面加工策略需要指定前倾角和侧偏角的数值，刀位没有充分优化；它可以使用平底刀和环形刀加工复杂曲面，与球头刀加工相比加工效率得到了一定提升。而北京航空航天大学提出的中点误差控制算法是一种高效的五轴数控编程算法，该算法可以获得每个刀触点处的最优刀位和整行刀轨上最大行宽。该算法在某航空企业的加工试验表明，与同尺寸的球头刀加工工艺相比，该方法能够提高加工效率2～10倍，明显提高模具曲面的加工表面质量，避免加工过切现象的发生。由于目前航空企业主要使用的CAD/CAM软件为达索公司的CATIA，因此有必要将该算法集成到CATIA软件的曲面加工模块，并在全厂进行推广应用，从而大幅提高复杂曲面的加工质量和加工效率，对于提升企业的技术水平具有十分重要的意义。

1 中点误差控制算法的基本原理

图1[9]所示为圆环刀具T加工自由曲面S（u，v）的刀具定位方式。设圆环刀具环心圆π的半径为R，刀具的小圆半径为r，最大允许欠切误差为δ。而Γ是设计曲面上的一条刀具驱动线。P1是Γ上的工件第1参考点。a是刀具在P1走刀方向的单位矢量，n是曲面在P1的单位法矢。在P1点沿着该点处曲面法矢n取点C2，它的位置为：rC2=rP1+（r+δ）n。设 e1=a，e3=n，e2=e3×e1，则（e1，e2，e3）构成刀具第二参考系。

图1 中点法的刀具预定位Fig.1 Tool pre-positioning with MPEC

建立刀具第二参考系（e1，e2，e3）后，刀具有绕 3个坐标轴的转动自由度，考虑到W型特征线中点已定位在控制误差带的上控制线，刀具绕e1转动会导致该点附近刀具产生欠切现象而影响行宽，故增加约束使C2为与S（u，v）法向偏置距离为（r+δ）n曲面的切触点，这样刀具还有绕e2，e3的2个转动自由度便能完成最终定位。剩余2个自由度可依次调整：刀具先绕e3轴旋转φ（旋转角），得到新的刀具坐标系（e1'，e2'，e3），再绕 e2'旋转θ（前倾角）得到新的坐标系（e1＂，e2'，e3'）,令o=（1 0 0）T，则刀心点在工件坐标系下坐标rO和刀轴矢量raxis为：

式中=，rP1为P1在工件坐标系下的位置矢量，M（φ，e3）为刀具绕e3旋转φ的变换矩阵，M（θ，e'2） 为刀具绕e'2旋转θ的变换矩阵。

2 基于CATIA二次开发中点误差控制算法实现

CATIA V5提供了5种开放性接口：标准格式导入/导出（standard format import/export）、使用 Automation API的宏命令模式、智能软件(Knowledgeware)、交互模式下的用户自定义特征、CAA V5 C++&Java API[10]。CAA(Components Application Architecture)，全称为组件应用架构，是基于组件的一种开发方法[11-13]。其采用面向对象的程序设计思想，完成对组件对象的组合和拓展，用户可以很方便地利用CAA对CATIA进行功能组合、拓展等二次开发工作，开发出来的模块与CATIA平台紧密结合，稳定性高，适合集成开发工作。

基于CAA组件架构思想，利用C++语言编程，并结合算法程序应用流程，将算法主程序与CATIA平台进行集成。通过采用公共数据库将算法应用过程中所有数据进行统一管理的方案，实现CATIA平台与CAM算法之间数据的灵活交换和准确传输，最终实现该算法程序在CATIA平台的集成和应用，如图2所示。

3 应用加工实例

3.1 加工对象

在直升机制造中，曲面模具大量用于钣金蒙皮件和复合材料构件的成型加工。模具曲面的加工质量直接影响最终产品质量，而加工效率也制约着产品的制造进度。本文以典型的曲面模具为加工对象，其结构由主体曲面和下陷结构组成，主体曲面加工精度要求为轮廓度±0.1mm，如图3所示。

3.2 工艺准备过程

3.2.1 曲面处理和分析

目前，该中点法仅适用于单张参数曲面的数控编程，即一次只能选一张参数曲面来计算刀轨。由于主体曲面原本是由多张面组合而成，可在CATIA软件中将其处理成一张参数曲面，从而用本文提出算法来实现刀轨的计算。这样做的好处是刀轨分布规则，减少了进退刀和空行程的时间，提高了加工效率。通过CATIA软件中的曲面处理功能对模具原始面进行提取和处理，形成与原始面近似的单张参数曲面，如图4所示。其误差范围为-0.018～0.008 mm，而最大误差在曲面周边，误差偏离小，因此可以将处理后的曲面作为后续加工对象。

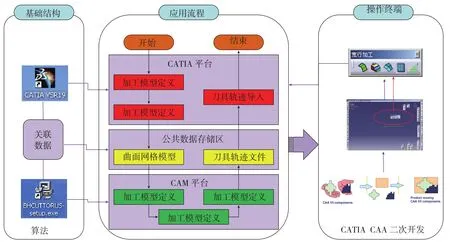
图2 基于CATIA二次开发平台中点法的实现流程Fig. 2 Implementation flow of MPEC based on CATIA secondary development

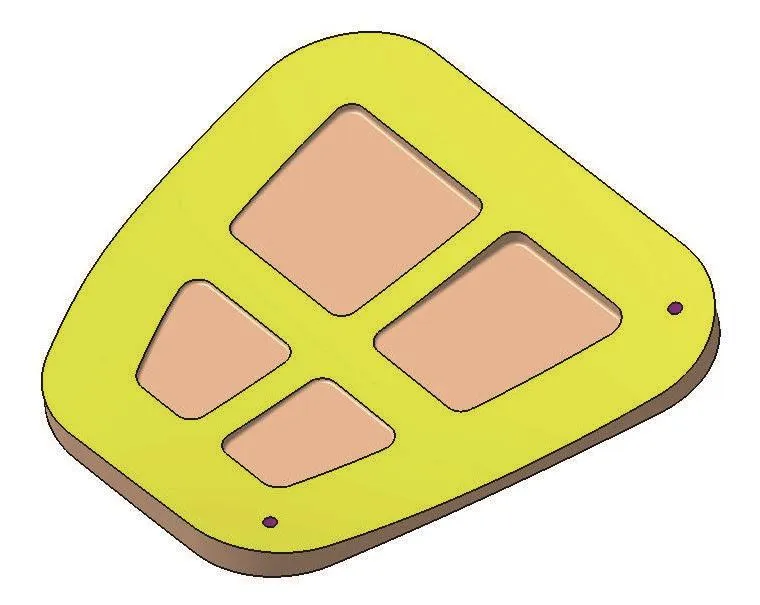
图3 航空曲面模具Fig.3 Aviation die surface

图4 处理后的单张参数曲面Fig.4 Treated single parametric surface

对上述处理后的参数面在CATIA软件进行曲面分析，分析结果如图5所示。从图中可以看出，该曲面大部分区域（图中黄色区域）的高斯曲率半径在（-1198～-19074）mm之间，因此该曲面为双曲抛物面，大部分曲面区域的曲率较小且变化平缓。

3.2.2 刀具轨迹生成

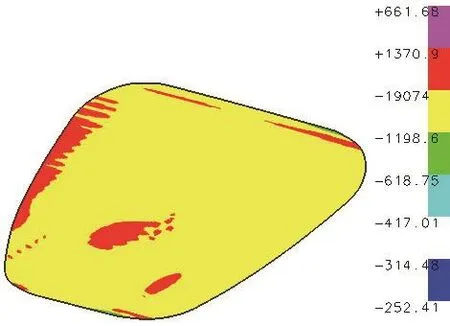
图5 处理后参数曲面的分析结果Fig.5 Analysis result of treated parametric surface

采用中点法来生成给定曲面的刀具轨迹，首先要对给定的曲面进行离散，然后根据给定的加工公差利用该算法生成相应的刀具轨迹。

（1）参数曲面离散。

曲面离散的疏密将直接影响到后续刀具轨迹。曲面主要通过设置UV方向的离散步长和弓高值来确定曲面离散的密度，密度越高刀轨计算越精确。而步长是决定离散密度的主要因素，对于此类开敞大型模具曲面，通常在1mm之内的曲率变化对刀位姿态几乎没有影响，因此一般设置步长最小值为1mm。该参数曲面的离散步长/弓高分别设为：U=1/0.1，V=1.5/0.1，即曲面以1×1.5规格网状离散，如图6所示。而刀位计算和刀轨规划时将以该离散点作为加工曲面的数据信息。

（2）刀具轨迹的生成。

根据加工曲面的分析结果，可以选择直径D=63mm、底刃圆角R=6mm的环形刀；选择刀具沿V向走刀，每条刀轨有400个刀位点，计算理论误差设定±0.01mm，二分法往增大方向优化前倾角，侧倾角不优化，具体参数设置如图7所示。计算结果为在满足给定加工误差条件下，在每个点位上刀具与加工曲面间都形成最大加工带度的刀位姿态，从而获得每个刀位点的切削宽度；每行400个离散点的刀位姿态计算出后，将以其中最小加工带宽作为该行的切削宽度。总共生成25条刀具轨迹，如图8所示。图9为其中一行刀轨切削行宽度确定的原理图，其中纵坐标代表参数行宽，横坐标代表离散点数。

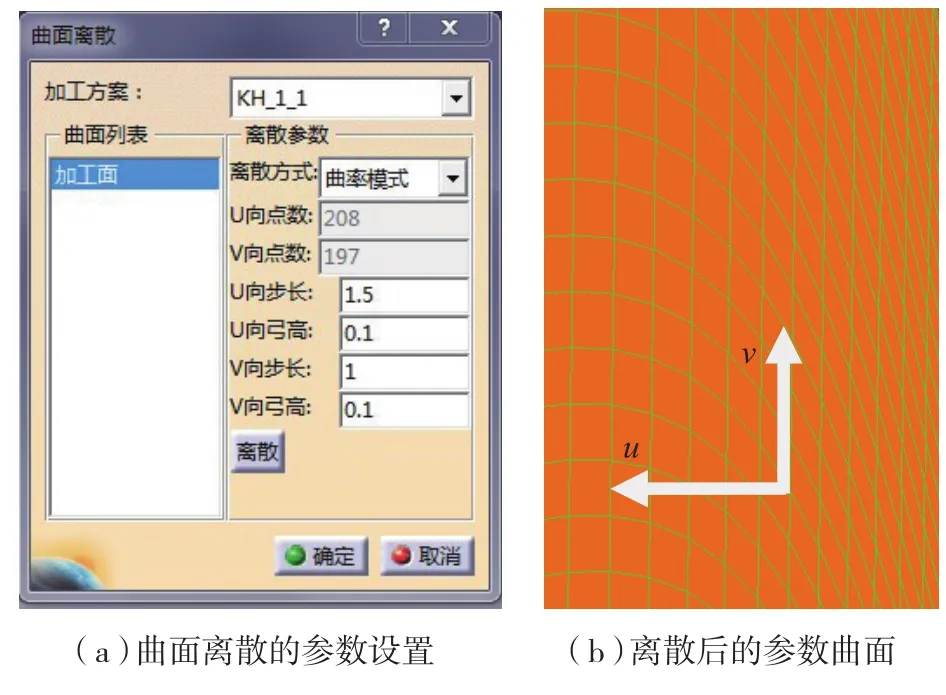
图6 参数曲面离散Fig.6 Discretization of parametric surface

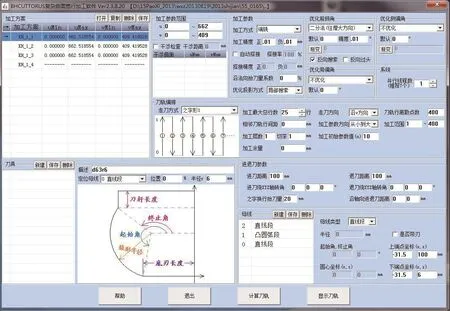
图7 刀轨生成参数设置Fig.7 Parameters setting for tool path generation

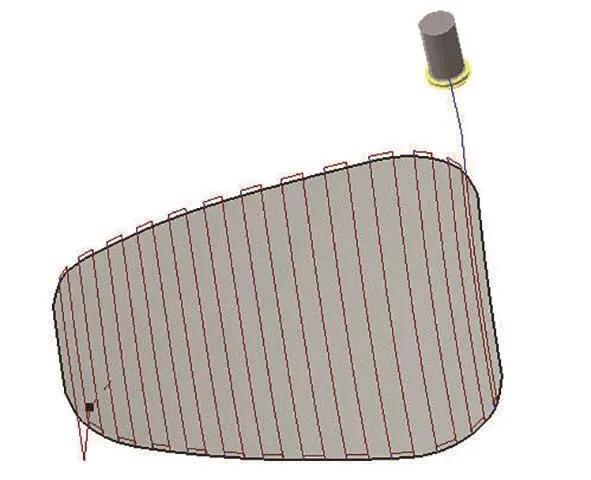
图8 中点法生成的刀具轨迹Fig.8 Tool path generated with MPEC

图9 切削行宽确定的原理图Fig.9 Principle of determining machining strip width

3.2.3 加工仿真

对上述生成的刀具轨迹，利用VERICUT软件进行加工仿真，仿真结果如图10所示。从图中可以看出，大部分加工区域都在给定的加工公差±0.01mm内，只有中间部分区域有0.02 mm局部残留误差，且加工曲面无任何异常过切。

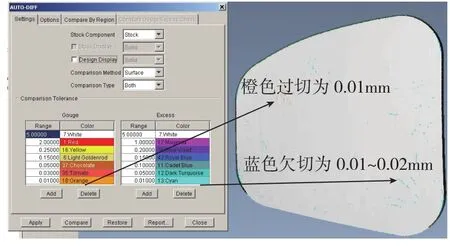
图10 VERICUT加工仿真结果Fig.10 Macining simulation result using VERICUT

3.3 加工试验

根据工件尺寸和车间现有机床情况，选择德国兹默曼公司FZ40型五轴龙门镗铣床。该机床的加工行程范围：X6000mm，Y3000mm，Z1500mm，A±95，C±220°；主轴转速S为（0～6000）r/min，进给速度 fz为（0～4000）mm/min。刀具选择与编程时刀具参数一致，即D63R6的环形刀。

加工过程中，主轴转速S=6000r/min，进给速度fz=3000mm/min，切深为（0.5～1）mm，切削行宽平均约为25mm，加工时间约为9min，加工过程如图11所示。

加工后的模具曲面，如图12所示。从图中可以看出，加工表面粗糙度较低，加工行距较宽，两行刀轨衔接处残留高度较小。与传统的球头刀行切工艺相比，该算法能够大幅缩短精加工曲面的后续抛磨量。

3.4 加工型面检测

在三坐标测量机上，对上述加工后的模具型面进行检测，具体检测点位置如图13所示。最终检测结果如图14所示。从图中可以看出，大部分区域加工误差在（-0.05～+0.05）mm之间，边缘部分区域加工误差在（0.06～0.08）mm之间。实际检测误差较大原因可能是由于安装误差、刀具误差、加工变形等因素的综合影响。

图11 模具曲面的加工过程Fig.11 Machining process of die surface

图12 模具曲面的加工效果Fig.12 Machined die surface

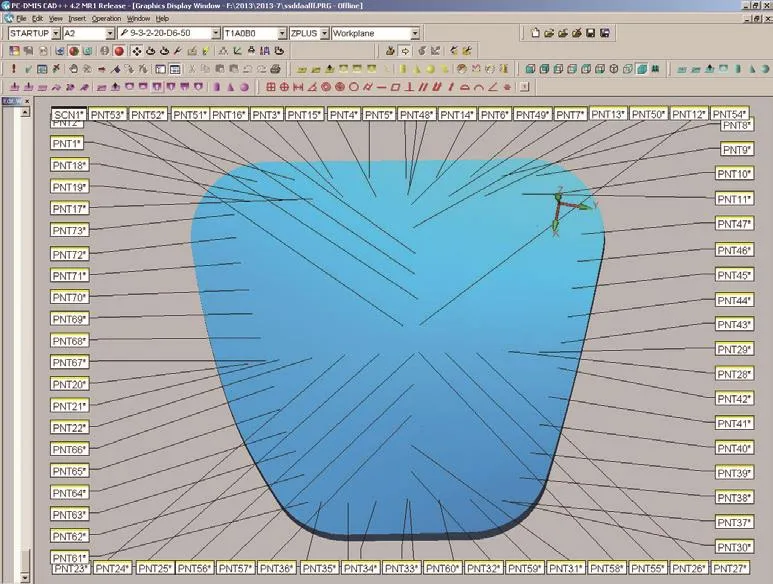
图13 加工曲面检测点位置Fig.13 Location of detection points on die surface

图14 曲面检测点加工误差Fig.14 Machining error of the detection points on die surface

4 结论

本文研究和分析中点误差控制算法的基本原理，在此基础上基于CATIA二次开发平台，通过利用C++语言编程来实现中点误差控制算法，并集成到CATIA V5的曲面加工模块。通过应用加工实例表明，该方法不仅能够大幅提高模具曲面的加工效率，而且改进了模具曲面的加工质量，并缩短后续手工抛磨的工作量。可见，该方法具有较强的工程应用价值，且能在航空企业内部进行推广应用。

[1] Vickers G W，Quan K. Ball-mills versus end-mills for curved surface machining. ASME Journal of Engineering for Industry，1989，111(2): 22-26.

[2] Jensen C G，Anderson D C. Accurate tool placement and orientation for finished surface. Machining J. Design and Manufacture，1993，3: 251-261.

[3] Kruth J P，Klewais P. Optimization and dynamic adaptation of the cutter inclination during five-axis milling of sculptured surfaces. CIRP Annals，1994，43(1): 443-448.

[4] Lee Y S. Admissible tool orientation control of gouging avoidance for 5-axis complex surface machining. CAD Computer Aided Design，1997，29(7): 507-521.

[5] Warkentin A，Bedi S，Ismail F. Five-axis milling of spherical surfaces. International Journal of Machine Tools and Manufacture，1996，36(2): 229-243.

[6] Warkentin A，Ismail F，Bedi S. Multi-point tool positioning strategy for 5-axis mashining of sculptured surfaces. Computer Aided Geometric Design，2000，17(1): 83-100.

[7] 金曼，张俐，陈志同. 圆环面刀具五坐标加工端点误差控制刀位优化. 北京航空航天大学学报，2006，32(09): 1125-1128.

[8] XU R，CHEN Z，CHEN W. Tool positioning algorithm based on the smooth tool path for 5-axis machining of sculptured surfaces. Chinese Journal of Mechanical Engineering，2011，5(24): 851-858.

[9] 陈志同，乐毅，徐汝锋. 中点误差控制宽行加工算法. 机械工程学报，2011，1(47): 117-123.

[10] 张敏，苏兰海，王君英.基于CAA的CATIA用户自定义特征创建.机械设计与制造，2008,9:87-88.

[11] 龙峰，樊留群.CATIA V5 二次开发技术初探. 淮阴工学院学报，2005，14(5):21-27.

[12] 潘爱民.COM原理与应用.北京:清华大学出版社，2000.

[13] 齐从谦，崔琼瑶. 基于参数化技术的设计方法研究. 机械设计与研究，2002，18(5):13-15.