混合流水车间调度问题的两阶段启发式算法

苏志雄，伊俊敏

(厦门理工学院管理学院， 福建 厦门 361024)

混合流水车间调度问题的两阶段启发式算法

苏志雄，伊俊敏

(厦门理工学院管理学院， 福建 厦门 361024)

针对以最小化makespan为目标的混合流水车间调度问题，提出了一种两阶段启发式算法。在算法设计中，借鉴求解常规流水车间调度问题的经验，定义了一种相邻交换的邻域结构。算法的第一阶段利用基于排列排序的Nawaz-Enscore-Ham(NEH)算法求得一个较好的初始解，第二阶段通过邻域搜索来提高解的质量。基于benchmark算例的仿真实验结果表明该算法的有效性，与NEH相比，77个算例的平均偏差降低了2.004%，且其运行时间不超过0.031 s。

生产调度；混合流水车间；NEH启发式算法；相邻交换

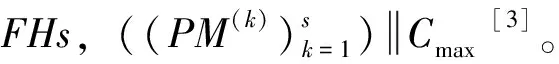
一、问题描述及分析

HFS调度问题是流水车间(flowshop，FS)调度问题和平行机调度问题的扩展与结合，其特点是所有阶段或部分阶段上存在并行设备。此类调度问题主要解决以下2个子问题：(1)工件排序即确定每台设备上的加工顺序；(2)设备指派即确定每个工件在各阶段的加工设备。与FS调度问题相比，各阶段的多机配置使得其复杂性与求解难度大大增加。由于常规HFS问题难于直接求解，大部分的调度算法采用分治思想来处理问题，即将原问题分解成若干个较小规模的子问题，然后求解这些子问题并将它们的解合并构成原问题的调度解。

到目前为止，最常用的分治法为：首先产生一个初始阶段的工件加工优先级顺序，然后再利用启发式方法来安排工件的生产，进而得到原问题的调度解。此种分治策略将搜索空间限制为初始阶段的n!个工件加工顺序，便于算法的设计与实现，并可以进一步扩展应用于大部分HFS变型问题。该策略首次于1995年由文献[11]提出并被应用于设计flowmult算法，并针对653个小规模问题进行测试，仿真实验的结果表明其有效性：90%的情况下可以找到最优解，并且98%的情况下可以找到与最优解相差5%以内的解。

文献[14]在分治策略的基础上，首次将常规FS的经典启发式调度算法(如CDS、NEH、TOW)用于求解常规HFS调度问题，其求解方法可以分为2个步骤：(1) 将问题虚拟为一个常规FS调度问题，然后利用基于排列排序的启发式算法进行求解得到一个工件加工优先级顺序；(2)考虑各阶段的平行机，基于步骤1得到的工件加工顺序，按照一定的规则进行设备指派，进而得到原问题的完整调度解。最后通过仿真实验说明了：采用第2种设备指派规则的NEH-T算法[15]取得了最好的效果。另外，分治策略也被应用于设计元启发式算法，如人工免疫算法[8]、变邻域搜索算法[9]、人工蜂群算法[10]等。

二、 NEHES算法

由以上分析可以看出，算法设计的关键与难点在于如何产生好的工件加工顺序及如何安排工件的生产。针对该问题特征，本文通过基于NEH的启发式算法来获得一个“较好”的初始解，然后再利用邻域搜索算法来提高解的质量。

1.编码与解码

本文采用排列(permutation)编码，它在文献[8～13]中得到了广泛使用。该编码的长度为n!，即取所有工件编号的排列作为解的表示，比如待加工工件n!的一个加工优先级顺序n!就是其相应的编码。值得注意的是，排列编码仅仅反映了初始阶段的工件加工顺序，因此在解码过程中需要考虑工件排序与设备指派。

在已有文献中，最常用的解码方法[9]可以描述为：(1)第一阶段按照编码确定工件加工顺序π1，后续阶段k按照先到先服务(firstcomefirstserved，FCFS)规则确定加工顺序πk；(2)在各阶段，按照对应的加工顺序将工件分配给最早可用设备(firstavailablemachine，FAM)。此外，文献[14]也给出了2种解码规则，通过对比说明了第2种规则的效果较好，该规则可以描述为：一次性将当前阶段的各工件分配给最晚空闲设备(lastfreemachine，LFM)使得该工件在下一阶段可以尽快完工，然后再安排下一阶段的调度。这两种解码方法均为解依赖型规则(solution-dependentrule，SDR)，不妨分别记为SDR1、SDR2。通过分析可以看出，它们的主要区别在于设备的选择，然而在FCFS规则下FAM与LFM不会影响到最终调度解的makespan值，即SDR1与SDR2具有相同的效果。与LFM相比，FAM更能平衡同阶段平行机间的负荷，因此本文的解码方法统一采用SDR1。

以10个工件5个阶段的算例j10c5a5为例[5]，对于给定的工件加工顺序π1={5,9,3,8,10,1,2,6,7,4}，分别按照SDR1、SDR2进行解码以生成完整的调度解。这两个调度解具有相同的makespan值(均为126)，对应的调度甘特图分别如图1、图2所示。

2.基于NEH的初始解

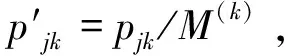
3.相邻交换

邻域搜索算法是一类改进型启发式算法，算法的每一步迭代是通过搜索当前解的邻域得到一个改进的解，其算法设计的关键在于邻域结构的选择。据粗略计算，邻域越大得到的最终解的精度越高，但是较大的邻域会使得每步迭代的时间变长。文献[16]在求解常规FS问题时发现，仅需简单交换已有排列中两个相邻工件，就可能得到一个较优的排列。由于本文采用的编码方法与常规FS问题一致，并且HFS作为FS的扩展，在邻域结构选择时可以借鉴其经验。因此，从第一阶段开始依次对各阶段上的工件采用相邻交换，直到当前阶段无法改进时就进入下一阶段。在阶段k上，相邻交换邻域就是交换所有可能的相邻工件的集合(规模为n-1)，对于邻域里面的解则需要通过SDR1规则对后续阶段进行解码以确定相应的makespan值，而邻域搜索算法的每一步迭代是将该邻域里面质量最好的解替换当前解，重复执行以上过程直至不再有改进为止。下面给出了相邻交换算法的伪代码：

ProcedureAdjacentSwap(πk)

gain=0

NewGain=OriginalCmax-NewCmax

ifNewGain>gain

gain=NewGain

endif

endfor

ifgain

πk=SwapRecord

Endif

三、仿真实验

在利用基于排列排序的NEH算法求解常规FS问题时，由于工件在各阶段上的加工顺序一致(同顺序)，只需在初始阶段上进行相邻交换邻域搜索。若采用上述策略来求解常规HFS问题，与之对应的算法是NEHES1算法，它是NEHES的特例。

本文的算法均采用Matlab语言进行编写，运行环境为Win8.1操作系统、i3-4130(3.40G)/4G的台式机。为了评价算法的有效性，采用以下3种指标：(1)百分比偏差(percentagedeviation，PD)，表示求得的Cmax与下界LB的偏差，即PD=(Cmax-LB)/LB×100；(2)计算时间CPU，以s为单位；(3)最优比率，表示求得最优解的算例个数占该算例集算例总数的比率。

1.测试数据

本文所采用的测试数据是Carlier和Néron提出的benchmark算例集[5]，其问题规模从10个工件5个阶段变化到15个工件10个阶段，且工件在各阶段的加工时间pjk∈[3,20]。根据阶段数、各阶段的平行机数、工件数等信息，这77个算例可以被分为4种类型，其中a类和b类问题的瓶颈阶段只有一台设备，c类问题的瓶颈阶段有二台平行机，而d类问题(除了j15c5d1)不存在瓶颈阶段即各阶段平行机数均为3台。例如，j15c5b2表示15个工件5个阶段、b类中的第2个算例。此外，根据求解难度，可以将这些算例分成两组：“易解”算例包括j10c10c*和所有的a类、b类问题；“难解”算例包括j10c5c*、j10c5d*、j15c5c*、j15c5d*[6]。

2.实验结果及分析

对于这两组易解、难解算例，分别采用NEH、NEHES1、NEHES独立运行1次，所得计算结果如表1、表2所示。

首先，从求解质量的角度进行比较。由表1可见，对于53个易解的算例，上述3种算法分别有29、35、36个算例达到了下界，对应的最优比率分别为54.717%，66.038%，67.925%，平均偏差分别为3.153%、2.056%、1.728%。结果表明，这3种方法的求解质量令人满意，尤其以NEHES为佳，与NEH相比，在最优比率和平均偏差这两个指标上分别提高了13.208%和1.425%，进而说明了本文设计的相邻交换邻域搜索的有效性。由表2可见，对于24个难解的算例，这3种算法都仅有1个算例达到了下界，平均偏差分别为11.659%，8.590%，8.378%，表明算例的求解难度对于其求解质量有较大程度的影响，虽然相邻交换邻域搜索使得平均偏差降低了3.281%，但是仍有一定的改进空间。由表1、表2可以得到，对于这77个算例，这3种算法的平均偏差分别为5.804%，4.093%，3.800%，与NEH相比，NEHES的平均偏差降低了2.004%。此外，与瓶颈指向的启发式算法[13]相比，对于这两组算例来说，NEHES在平均偏差方面分别降低了0.124%、1.805%。

其次，从求解效率的角度进行比较。由于NEHES是以NEH、NEHES1为基础，进一步进行后续阶段的相邻交换邻域搜索，因此其计算时间更长。由表1、表2可以看出，对于这两组算例NEHES的平均计算时间也仅为0.008、0.009s，且最长不超过0.031s，进而表明3种算法均具有较高的求解效率。

表1 易解算例的计算结果

续表1

表2 难解算例的计算结果

四、结论

本文针对最小化makespan的HFS问题展开研究，主要取得了以下结果：(1)通过问题分析和对已有算法的总结，基于分治思想提出了一种两阶段启发式算法，该算法利用基于排列排序的NEH算法求得一个较好的初始解，然后再利用邻域搜索来提高解的质量；(2)在算法设计中，采用排列编码将搜索空间限制为初始阶段的n!个工件加工顺序，并借鉴求解常规FS问题的邻域结构，设计了一种相邻交换邻域搜索算法；(3)NEHES是以NEH、NEHES1为基础，进一步进行后续阶段的相邻交换邻域搜索，通过较长的计算时间来获得较好的求解质量。基于benchmark算例的实验结果，对于这两组算例NEHES的平均偏差仅为1.728%，8.378%，与NEH相比分别提高了1.425%，3.281%，且其平均计算时间也仅为0.008，0.009 s。这也表明了本文提出的NEHES算法能够有效求解常规HFS问题，并具有满足实际需求的计算效率，但是对于难解算例，其求解质量仍有一定的改进空间。

[1]李铁克，苏志雄.炼钢连铸生产调度问题的两阶段遗传算法[J].中国管理科学，2009，17(5):68-74.

[2]RUIZR，VZQUEZ-RODRGUEZJA.Thehybridflowshopschedulingproblem[J].EuropeanJournalofOperationalResearch，2010，205(1):1-18.

[3]HOOGEVEENJA，LENSTRAJK，VELTMANB.Preemptiveschedulinginatwo-stagemultiprocessorflowshopisNP-hard[J].EuropeanJournalofOperationalResearch，1996，89(1):172-175.

[4]GUPTAJND.Two-stagehybridflowshopschedulingproblem[J].Journaloftheoperationalresearchsociety，1988，39(4):359-364.

[5]CARLIERJ，NÉRONE.Anexactmethodforsolvingthemulti-processorflow-shop[J].RAIRO-OperationsResearch，2000，34(1):1-25.

[6]NÉRONE，BAPTISTEP，GUPTAJND.Solvinghybridflowshopproblemusingenergeticreasoningandglobaloperations[J].Omega-InternationalJournalofManagementScience，2001，29(6):501-511.

[7]PANQK，WANGL，LIJQ，etal.Anoveldiscreteartificialbeecolonyalgorithmforthehybridflowshopschedulingproblemwithmakespanminimization[J].Omega-InternationalJournalofManagementScience，2014，45:42-56.

[8]CHUNGTP，LIAOCJ.Animmunoglobulin-basedartificialimmunesystemforsolvingthehybridflowshopproblem[J].AppliedSoftComputing，2013，13(8):3 729-3 736.

[9]LIJQ，PANQK，WANGFT.Ahybridvariableneighborhoodsearchforsolvingthehybridflowshopschedulingproblem[J].AppliedSoftComputing，2014，24:63-77.

[10]CUIZ，GUXS.Animproveddiscreteartificialbeecolonyalgorithmtominimizethemakespanonhybridflowshopproblems[J].Neurocomputing，2015，148(1):248-259.

[11]SANTOSDL，HUNSUCKERJL，DEALDE.Flowmult:permutationsequencesforflowshopswithmultipleprocessors[J].JournalofInformation&OptimizationSciences，1995，16(2):351-366.

[12]SANTOSDL，HUNSUCKERJL，DEALDE.Anevaluationofsequencingheuristicsinflowshopswithmultipleprocessors[J].Computers&IndustrialEngineering，1996，30(4):681-691.

[13]屈国强.瓶颈指向的启发式算法求解混合流水车间调度问题[J].信息与控制，2012，41(4):514-521，528.

[14]GUINETA，SOLOMONM.Schedulinghybridflowshopstominimizemaximumtardinessormaximumcompletiontime[J].InternationalJournalofProductionResearch，1996，34(6):1 643-1 654.

[15]TAILLARDE.Someefficientheuristicmethodsfortheflowshopsequencingproblem[J].EuropeanJournalofOperationalResearch，1990，47(1):65-74.

[16]DANNENBRINGDG.Anevaluationofflowshopsequencingheuristics[J].ManagementScience，1977，23(11):1 174-1 182.

(责任编辑 雨 松)

A Two-phase Heuristic Algorithm for Hybrid Flow Shop Scheduling Problems

SU Zhi-xiong,YI Jun-min

(School of Management,Xiamen University of Technology,Xiamen 361024,China)

To solve the hybrid flow shop scheduling problems with makespan criterion,a two-phase heuristic algorithm is presented. In the algorithm design,an adjacent swap neighborhood structure is proposed by using the experience of flow shop scheduling problems for reference. In the first stage,a good initial solution is found by the Nawaz-Enscore-Ham (NEH) algorithm with permutation schedules.In the second stage,the neighborhood search is used to quickly improve the solution obtained. Last,the experimental results of benchmark instances indicate the effectiveness of the proposed algorithm.Compared with NEH algorithm,the average percentage deviation value by this method is decreased by 2.004%,and the running time is no longer than 0.031 s.

production scheduling;hybrid flow shop;NEH heuristic algorithm;adjacent swap

2015-04-07

2015-05-20

国家自然科学基金项目(71371162)；福建省自然科学基金项目(2014J01271)；厦门理工学院高层次人才项目(YSK10009R)

苏志雄(1980-)，男，讲师，博士，研究方向为生产计划与调度、运输调度，E-mail:z.su@163.com

F273；TP278

A

1673-4432(2015)04-0019-07