基于多涡卷Jerk-Chua混沌和自编码的扩频码构造方法
张晓蓉,吴成茂,李文学
(1.西安邮电大学电子工程学院,陕西西安710121;2.解放军理工大学国防工程学院,江苏南京210007)
基于多涡卷Jerk-Chua混沌和自编码的扩频码构造方法
张晓蓉1,吴成茂1,李文学2
(1.西安邮电大学电子工程学院,陕西西安710121;2.解放军理工大学国防工程学院,江苏南京210007)
为了提高扩频通信系统信息传输的可靠性和安全性,提出一种基于复合多涡卷Jerk-Chua混沌与自编码相融合的扩频码构造算法。首先引用二维Henon变换和离散标准映射的构造思想产生一种新的非线性融合函数,其次通过该融合函数将复合多涡卷Jerk-Chua混沌产生的随机序列与自回归自编码随机序列相融合产生高质量复合随机序列作为新的扩频码。最后通过Matlab仿真测试表明,该算法相比现有方法得到的随机序列复杂度更高、随机性和相关性更好,应用于扩频通信系统中的误码率得到了一定改善,能够满足高安全性和高动态变化环境要求的通信系统信息安全保密的传输。
复合多涡卷Jerk-Chua混沌;自回归自编码;Henon变换;标准映射;误码率
0 引 言
扩频通信技术是一种信息传输方式。扩频通信主要包括直接序列扩频、跳频扩频和跳时扩频3大类。扩频通信广泛应用于现代移动通信和军事作战指挥系统等领域。直接序列扩频通信是扩频通信中应用最为广泛的一种通信方式,其关键在于如何构造性能优良的扩频码序列。在当今电磁环境越来越恶劣的情况下,扩频通信技术能够大大提高通信系统的抗噪声干扰性能。混沌系统由文献[1]提出,并广泛应用于军事、控制等众多领域。近十多年来,混沌理论在信息安全、通信等方面也取得了长足的发展,特别是当前的混沌通信已引起众多学者的高度关注。混沌是一种特殊的非线性动力学系统。由于混沌序列具有优良的特性已经应用到了航空航天、信息处理、模糊和神经网络的融合,并且由于混沌序列的高度伪随机性使得序列之间永久不会重复,所以众多混沌扩频系统能够共用同一信道,这样使得频率资源利用率得到了很大地提高[2]。目前有大量学者研究了具有良好随机性的混沌序列在扩频通信中的应用[3-9],如Logistic型[3-4]、Chebyshev型[5]、Tent型[6]、分段Logistic型[7]、正交Logistic[8]、分段Skew Tent型[9]等构造的扩频序列及其在扩频通信中的应用。这些传统的混沌随机序列尽管具有很好的相关性和较理想的平衡性,但是其保密性能差,复杂度也不是很高。因此,研究人员致力于构造更复杂的混沌系统,提出了多涡卷混沌,该系统相比于普通的单涡卷混沌系统,具有更加复杂的动力学行为和长期不可预测性,可以更好地应用于扩频通信领域。文献[10]利用一种基于切换控制的方法实现了Lorenz系统族之间的复合。随着研究的深入,人们将不同类型的混沌系统复合成一个系统[11],如不同两涡卷混沌系统的复合、不同多涡卷混沌系统的复合,使得复合后系统的行为更加复杂,极大地增强了系统抗破解能力,从而具有很好的应用前景。文献[12- 14]对不同混沌序列的性能进行研究,表明这些混沌序列具有良好的随机性、相关性等可以满足扩频通信的需要,但是同时它们实际上也是确定的,在通信过程中可能被窃听、复制,对传输信息安全有潜在的威胁。近年来,自编码[15]成为扩频序列的重要构造方法,已在直扩和跳频通信系统中得到成功应用[16- 17]。文献[18- 19]研究表明自编码序列所具有良好的相关特性、游程特性、平衡性和线性复杂度,正逐渐被大量扩频通信系统采用。文献[20]把基于自回归(auto regressive,AR)滤波器提取的自编码扩频技术应用于卫星测控通信中,不仅可以降低传输信号的截获率,而且提高了通信的隐蔽性和安全性。但是,自编码扩频序列本身存在复杂性低的缺陷还未引起学者们的重视。为了进一步完善自编码扩频通信系统的安全性和可靠性。于是,本文构造了新的非线性融合函数将复合多涡卷Jerk-Chua混沌产生的随机序列与AR自编码序列相融合获得一种复合随机序列作为新的扩频码。该扩频码不仅具有复合多涡卷Jerk-Chua混沌独特的动力学特性,同时还具有AR自编码序列良好的信源关联性以及较高的伪随机性能,满足了信息对抗环境扩频通信对高安全性能的要求。通过对复合多涡卷混沌序列、AR自编码序列以及二者相融合序列特性的比较分析表明,本文所提出的复合扩频码构造算法是有效的,其相关性、随机性和复杂性等都得到了一定程度改善,同时其通信误码率也有了显著降低,提高了扩频通信系统的可靠性和安全性,将在通信领域有一定的研究意义和良好的应用前景。
1 复合多涡卷Jerk-Chua混沌
混沌是非线性确定系统由于内在随机性而产生的外在复杂表现,是一种特殊的动力学系统。近十多年来,混沌理论在图像加密、信息安全、通信等方面也取得了长足的发展[2122],特别是当前的混沌通信已受到广大学者的高度重视。
由于传统混沌映射的控制参数取值范围小、混沌特性弱和复杂度低等缺陷,并不利于扩频通信信息传输的可靠性和安全性,因此,文献[11]提出了多涡卷混沌。本文主要引用复合多涡卷Jerk-Chua混沌吸引子进行研究。复合多涡卷Jerk-Chua混沌吸引子的状态方程为
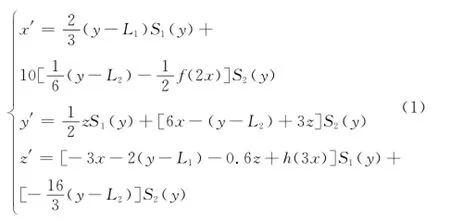
式中,L1和L2分别为多涡卷Jerk系统和多涡卷Chua系统在y方向的平移量,L1=0.58,L2=-0.55;f(x)=0.3x-0.15[sgn(x)+sgn(x-1)+sgn(x+1)]h(x)=sgn(x)+sgn(x-2)+sgn(x+2)复合多涡卷Jerk-Chua混沌吸引子的切换控制器为

式中,常数也不是唯一的而且通过修改切换控制器可以控制混沌吸引子呈现的顺序。文献[11]选取初始值为(0.3,0.1,0.1)时,测得复合多涡卷Jerk-Chua混沌系统的最大Lyapunov指数为8.0909,而本文测得其最大Lyapunov指数为6.4240,亦说明复合多涡卷Jerk-Chua系统处于混沌状态。
2 自编码序列构造
自编码扩频通信(self encoded spread sprectrum communication,SESS)是美国学者Lim Nguyen在1999年提出的一种新颖通信技术。它采用了自适应滤波器的滤波模型原理并利用其逆过程的线性滤波法从不断的信源序列中提取一种伪随机序列作为扩频码应用于扩频通信[23],而不是使用传统通信系统的伪随机序列发生器来产生扩频码序列,保证了扩频码与传输信息紧密关联且随信源信息发生改变而改变,极大地提高了抗扩频码检测能力,保证了扩频码序列的随机性、动态可变性、通信隐蔽性和低截获率,但是这种自编码扩频序列存在复杂性低的缺陷。
3 复合随机序列构造方法
为了构造性能优良的扩频序列,本文针对传统混沌特性较弱和复杂度低的缺点,提出了复合多涡卷混沌系统,将其与线性滤波法产生的AR自编码随机序列通过本文构造的非线性融合函数相融合,获得一种兼有两种随机序列优点的新复合随机序列。
3.1 复合随机序列融合原理
一般而言,将两个离散随机序列融合为一个离散随机序列的典型方法有异或、同或等运算法,但这些方法已在传统密码学等领域得到广泛应用,由于异或、同或运算具有拟线性运算特性,缺乏抗差分攻击等的能力。为此,本文探讨了两个离散随机序列融合新方法,其融合思想如图1所示。其原理描述如下:首先将二值离散随机序列分割成长度为8的子块,将每个子块转化为0~255的整数值。将两个二值离散随机序列所对应的整数序列作为二元非线性函数的输入,其二元非线性函数的一个输出作为两个整数变量的融合输出结果,另一个输出反馈到二元非线性函数的输入端,与其中一个输入整数值相加后的值与256取模得到的余数作为二元非线性函数的一个输入变量。最后,将二元非线性函数输出的整数序列通过二进制转化并获得最终融合的二值离散随机序列,将其作为扩频码应用于扩频通信。

图1 融合原理框图
3.2 复合随机序列融合算法
为了实现二值离散随机序列的融合需要,本文利用混沌理论中的一种非线性且可逆的Henon混沌变换和离散标准映射的构造思想,构造新的非线性可逆变换作为融合函数,解决现有二值序列异或、同或融合所存在的缺陷。为此,下面首先介绍二维Henon变换和离散标准映射,其次提出新的非线性可逆变换。
3.2.1 非线性可逆变换的构造
为了提高扩频通信信息传输的安全性和可靠性,本文以可逆Henon映射和离散标准映射[2425]为基础,构造新的非线性可逆变换。
首先,二维Henon变换可描述为[26]

式中,a,b,c为系统参数。当a=1.4,b=1,c=0.3时,系统(3)处于混沌状态,且当c=1时,系统在运动中保持相平面积不变。
其次,标准映射可描述为

式中,k为一正常数,易将表达式推广为一般形式为

为了满足扩频通信信息安全保密的传输,可将表达式(5)离散为

本文利用以上可逆Henon映射变换和离散标准映射的构造思想,获得一种新的二维非线性可逆变换表达式为

式中,N是正整数。针对本文应用需要,选取N=256。利用式(7)可解决两个整数序列的非线性融合问题。
3.2.2 复合离散随机序列融合算法
利用本文构造的新的非线性可逆变换实现两个二值离散随机序列融合,下面给出具体融合算法步骤。
假设融合的两个二值离散随机序列长度为N=8N1,式中,N1是正整数。
步骤1 利用复合多涡卷混沌系统和线性滤波器产生产生两个二值离散随机序列分别为k1(l),k2(l)(l=1,2,…,N),将其整数化处理为k*1(l),k*2(l)∈{0,1,…,N-1}(l=1,2,…,N1)。其详细过程如下:
首先本文选取复合多涡卷混沌系统的初始值为(0.3,0.1,0.1),进行重复迭代复合多涡卷混沌系统1 000次并将产生值扔掉,然后生成长度为N1的实数序列x*b(l)∈(0,1)(l=1,2,…,N1),将其整数化处理为

最后,对b*(l)处理为

步骤2 两个整数化随机序列k*1(l),k*2(l)(l=1,2,…,N1)融合产生新的整数化随机序列z*(l)(l=1,2,…,N1)过程如下:
若l=1时,利用本文构造的新的非线性可逆变换产生融合值z*(1)为

否则,利用本文构造的新的非线性可逆变换产生融合值z*(l)(l=2,3,…,N1)为

式中,l=2,3,…,N1;函数g(x,y)=x⊕y。
步骤3 将融合所得整数序列z*(l)(l=1,2,…,N1)进行二进制转化并获得长度为N的复合离散伪随机序列,将其用作扩频码实现扩频通信。
4 复合随机序列特性分析
为了广泛应用本文所产生的复合随机序列作为扩频码实现扩频通信,需要对复合随机序列的Lyapunov指数、相关性、随机复杂性等进行分析。
4.1 Lyapunov指数
Lyapunov指数是判断初始值敏感,即混沌现象的一个定量的指标,它表示相邻轨线间的平均发散率,是一个统计平均量。文献[11]利用龙格库塔数值模拟方法,设定系统初值为(0.3,0.1,0.1)求解多种复合混沌系统的Lyapunov指数,而本文选择Lyapunov指数为6.424 0的复合多涡卷Jerk-Chua混沌吸引子来构造新复合扩频码序列。下面仿真新复合扩频码序列的Lyapunov指数谱。如图2所示。
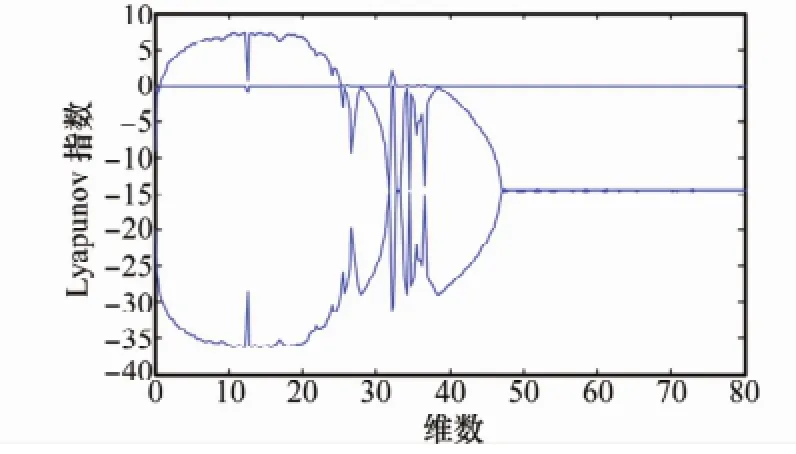
图2 Lyapunov指数谱
从图2可以看出,产生新复合扩频序列的最大Lyapunov指数达到7.232 8,这说明该方法所生成的随机序列具有很高的复杂性和较高的初值敏感性,保证了扩频通信信息传输的可靠性和安全性。
4.2 相关性分析
在扩频通信系统中,衡量一个扩频序列的重要技术指标是由序列的相关特性决定,即扩频码序列的相关性能的好坏与扩频通信系统的抗多径干扰能力有直接影响。设二值随机序列的长度为N,则该二值序列的自相关系数定义为

互相关系数定义为

式中,k为步长参数,相关系数的值与步长k有关,当步长变化时,如果相关系数变化越小,说明对应二値随机序列的随机性越好。对复合多涡卷Jerk-Chuan混沌所产生随机序列,AR自编码序列以及本文所产生复合扩频序列的相关性进行测试分析,如图3~图5所示。

图3 复合多涡卷Jerk-Chua序列相关性
为了进一步了解上述3种随机序列的自相关和互相关特性,取序列长度为1 000的随机序列,求其自相关和互相关的最大值、最小值,其详细情况如表1所示,其中自相关的最大值是除去1之外的最大值。

图4 AR自编码序列的相关性
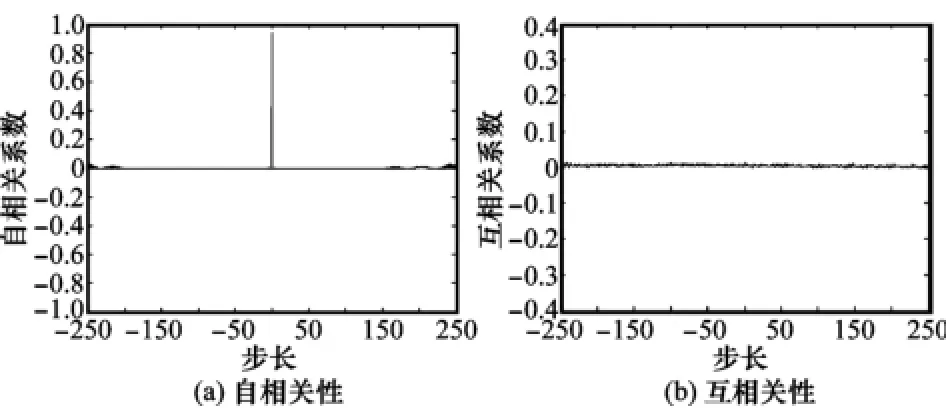
图5 复合扩频序列的相关性

表1 不同随机序列的自相关和互相关值
从上述3种不同的随机序列相关波形图表明,当步长参数k≠0时,上述3种不同随机序列的相关系数均接近于0,但是总体而言,相对于复合多涡卷Jerk-Chua混沌和自编码序列的相关性能,本文新构造的复合扩频码序列的相关性更好,随机性更优越。同时,从表1所示的自相关和互相关的最大值和最小值来看,本文所建议的新复合随机序列相关特性较为稳定,且波动更小,能满足扩频通信和图像加密等众多领域应用需要。
4.3 复杂度分析
一般而言,除常采用Lyapunov指数、维数来度量混沌系统的随机特性外,学者们提出采用近似熵、模糊熵等来描述混沌轨道随时间演化信息的产生率来度量混沌序列的复杂程度。计算近似熵的方法如下。
步骤1 给定一个长度为N时间序列k(1),k(2),…,k(N)按顺序将其组成一个m维的向量集X(i),即X(i)=[k(i),k(i+1),…,k(i+m-1)],其中i=1,2,…,N-m+1。
步骤2 计算任意向量X(i)与其余向量X(j)之间的距离d[X(i),X(j)]为d[X(i),X(j)]=max|x(i+k)-x(j+k)|,其中k=0,1,…,m-1,即两向量对应元素之间差值绝对值的最大值就是两向量之间的距离。
步骤3 给定阈值r(r>0),对于每一个i值,记录满足条件d[X(i),X(j)]<r的个数。把这个值与N-m的比值定义为
步骤4 对每一个可能的i值,计算Cmi(r)的自然对数,这些对数的平均值定义为


ApEn表示向量集随着m增大信息产生的概率,产生信息的概率越大,Ap En值就越大,即时间序列的复杂度越大。
按照上述方法分别求出复合多涡卷混沌序列、自编码序列和复合随机序列的近似熵。计算结果如表2所示。

表2 不同随机序列的近似熵比较
从表2中3个不同随机序列所对应的近似熵值来看,本文所建议新复合随机序列的近似熵值相对较大,说明其复杂度更高。同时上述近似熵的值表明本文建议的新复合随机序列也具有潜在混沌优势,亦说明了该复合随机序列应用于扩频通信信息传输是可行的,高复杂性满足了通信系统抗干扰、抗侦破的要求,能够保证信息高安全保密传输。
5 扩频通信应用仿真分析
本文采用直接序列扩频通信方式(direct sequence spread spectrum communication,DS-SS)方式[28],为了进一步验证本文建议的方法所产生的复合随机序列所具有的良好特性,在高斯白噪声信道下(设置信道的信噪比为5 dB),测试不同扩频码通信时的误码率,即分别用复合多涡卷Jerk-Chua混沌映射、线性滤波法和非线性融合算法生成的随机序列作为扩频码进行数据的传输。其原理如图6所示,在扩频部分,首先传输一个二进制随机数字序列,经过二进制相移键控(binary phase shift keying,BPSK)调制后,其次采用本文方法构造的复合随机序列对其进行扩频调制,产生扩频发送信号。在解扩部分,利用与发送端同步的扩频码序列对扩频信号进行解扩,将宽带信号恢复到很窄的频带内,再用BPSK解调,从而恢复原始的二进制数字信号。

图6 DS-SS原理图
通过Matlab模型仿真系统进行扩频通信,计算恢复后的信息与原始信息的误码率如图7所示。为了进一步得到较准确的结果,本文选取传输比特数从1.0×103逐渐增大到1.0×104,并重复多次求通信误码率的平均值。其测试结果如表3所示。

图7 误码率随比特数的关系曲线
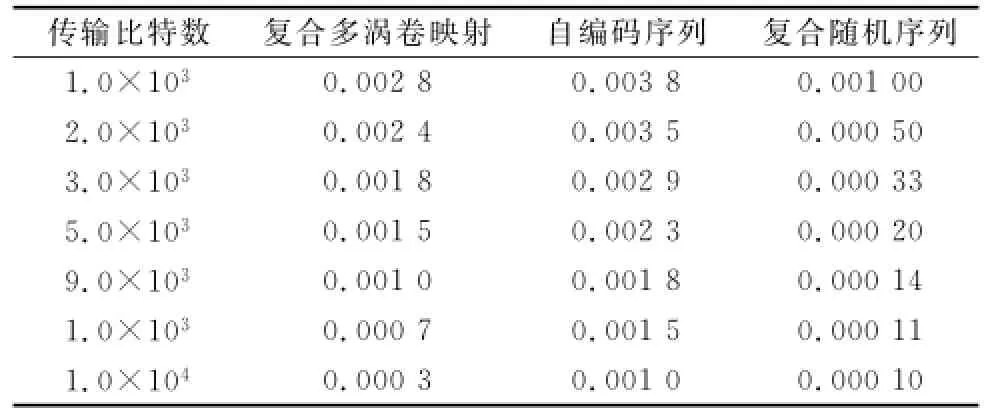
表3 新复合随机序列的传输误码率
图7仿真结果表明,不同随机序列随着传输比特数增大,误码率降低,明显可知本文构造的复合随机序列的误码率在相同条件下最低。由表3的测试结果可得,复合多涡卷Jerk-Chua混沌序列作为扩频码的通信误码率平的均值约为0.001 5,自编码序列的扩频误码率平均值为0.002 4,而本文采用融合方法产生的扩频误码率的平均值为0.000 34,显而易见复合多涡卷Jerk-Chua混沌序列和自编码序列的误码率相对较低,表明了本文建议的方法所构造的复合扩频码序列的误码率性能得到了很大地改善,并且使得通信系统抗干扰能力、安全性增强,保证了数据信息传输的保密性和可靠性。
6 结 论
本文以混沌和自编码系统为基础,提出复杂度较高的高维复合多涡卷混沌序列和与信源相关联的自编码序列相融合的算法构造复合随机序列,其中引用标准映射和可逆Henon混沌变换的思想构造非线性融合变换作为融合函数。该方法得到的复合随机序列的相关特性、随机特性较好,复杂度较高。最后在扩频通信系统进行误码率仿真,结果表明,本文算法构造的扩频序列的误码性能得到了极大地改善,保证了高动态通信条件下信息可靠安全传输。也证实了本文构造的复合随机序列在图像加密、保密通信等领域具有更大的优势,具有一定的研究和实用价值。
参考文献:
[1]Lorenz E N.Deterministic nonperodic flow[J].Journal of the Atmospheric Sciences,1963,20(2):130- 141.
[2]Huang C S,Li X L.Spread spectrum communication system and its performance analysis based on chaos[J].Communications Technology,2008,42(12):37- 39.(黄乘顺,李星亮.基于混沌的扩频通信系统及性能分析[J].通信技术,2008,42(12):37- 39.)
[3]Zhang Z Y,Xiao W,Ye J L.Performance enh-ancement of DS/SS system using chaotic spreading sequence[J].Computer Application,2007,27(1):135- 138.(张志禹,肖伟,叶嘉鲁.使用混沌扩频序列增强DS/SS系统性能[J].计算机应用,2007,27(1):135- 138.)
[4]Yu J F,Yang W G,Lu W T,et al.Generation and performance analysis of digital chaotic sequence from surjective Logistic-map[J].Telecommunication Engineering,2013,53(2):140- 145.(余金峰,杨文革,路伟涛,等.满映射Logistic数字混沌序列的产生及性能分析[J].电讯技术,2013,53(2):140- 145.)
[5]Kohda T,Tsuneda A.Even-and odd-correlation functions of chaotic Chebyshev bit sequences for CDMA[C]∥Proc.of the IEEE Internation Symposium on Spread Spectrum Techniques and Applications,1994:391- 395.
[6]Jessa M.The period of sequences generated by tent-like maps[J].IEEE trans.on Circuits System-I,2002,49(1):84- 88.
[7]Zhang W,Xie H M,Wang B P.Novel piecewise Logistic chaotic spread spectrum communication algorithm[J].Computer Science,2013,40(1):59- 62.(张薇,谢红梅,王保平.一种新型的分段Logistic混沌扩频通信算法[J].计算机科学,2013,40(1):59- 62.)
[8]Ihan M,Philip,Andi S.Chaos codes vs.orthogonal codes for CDMA[C]∥Proc.of 10th International Symposium on Spread Specturm Techniques and Applications,2010:189- 193.
[9]Wang B P,Li W K,Wu C M,et al.Improved piecewise skew tent map and its application in spread spectrum communications[J].Infrared and Laser Engineering,2013,42:(10):2772- 2777.(王保平,李文康,吴成茂,等.改进分段Skew Tent映射及其在扩频通信中应用[J].红外与激光工程,2013,42(10):2772- 2777.)
[10]Zhang C X,Yu S M.Design and implementation of compound chaotic attractors[J].International Journal of Bifurcation and Chaos,2012,22(5):125- 132.
[11]Ai X X,Sun K H,He S B.Compound attractors between different chaotic systems[J].Acta Physics Sinica,2014,63(4):1-8.(艾星星,孙克辉,贺少波.不同类型混沌吸引子的复合[J].物理学报,2014,63(4):1- 8.)
[12]Luo S J,Qiu S S,Chen X.A way to complexity analysis of chaotic pseudo random sequence[J].Journal of South China University of Technology,2010,38(1):18- 21.(罗松江,丘水生,陈旭.一种混沌伪随机序列复杂度分析方法[J].华南理大学学报,2010,38(1):18- 21)
[13]Wang G Y,Yuan F.Cascade chaos and its dy-namic characteristics[J].Acta Physics Sinica,2013,62(2):1- 9.(王光义,袁方.级联混沌及其动力学特性研究[J].物理学报,2013,62(2):1- 9.)
[14]Li Z,Cai J P,Chang Y L.Determining the co-mplexity of FH/ SS sequenceby approximate Entropy[J].IEEE Trans.on Communications,2009,57(3):812- 820.
[15]Nguyen L.Self-encoded spread spectrum co-mmunications[C]∥Proc.of the IEEE Military Communications Conference,1999:182- 186.
[16]Fei Y,Zhong L L.A new method to produce SESS codes with the algorithm of estimation of PSD[C]∥Proc.of the International Conference on Communication,Circuits and Systems,2004:117- 120.
[17]Fahey S F,Nguyen L.Self-encoded spread spectrum communications with FH-MFSK[C]∥Pro.of the 2nd International Conference on Advances in Satellite and Space Communications,2010:82- 89.
[18]Wei M,Li Z L,Yin F.Analysis and simulation of AR-SESSsystem performance[C]∥Proc.of the 2005 International Conference on Communications,Circuitsand Systems,2005:160- 164.
[19]Casey L D.Perormance of self-encoded spread spectrum under worst-case jamming[D].USA:University of Nebras ka-Lincoln,2010.
[20]Liu H F.A satellite TT&C telecommunication technology based on AR-SESS[J].Information Security and Communications Privacy,2008,30(8):57- 60.(刘辉峰.基于AR自编码扩频的卫星测控通信技术[J].信心安全与通信保密,2008,30(8):57- 60.)
[21]Alvarez G,Montoya F,Romera M,et al.Breaking two secure communication systems based on chaotic masking[J].IEEE Trans.on Circuits and Systems-II,2004,51(10):505- 506.
[22]Zhang H,Wang X F,Li Z H,et al.A new image encryption algorithm based on chaos system[C]∥Proc.of the International Conference on Robotics,Intelligent Systems and Signtal,2003:778- 782.
[23]Zhang X R,Wu C M.Construction of spreading code based on nonlinear fusion of chaotic mapping and self-coded method[J].2014,54(6):769- 774.(张晓蓉,吴成茂.基于混沌与自编码相融合扩频码的构造[J].电讯技术,2014,54(6):769- 774.)
[24]Fridrich J.Image encryption based on chaotic maps[J].IEEE Trans.on Computational Cybernetics and Simulation,1997,16(2):1105- 1110.
[25]Li C G,Han Z Z,Zhang H R.An image encryption algorithm based on random key and quasi-standard map[J].Chinese Journal of Computer,2003,26(4):465- 470.(李昌刚,韩正之,张浩然.一种基于随机密钥及”类标准映射”的图像加密算法[J].计算机学报,2003,26(4):465- 470.)
[26]Zhang H,Wang X F,Li Z H,et al.A fast image encryption algorithm based on chaos system and henon map[J].Journal of Computer Research and Development,2005,42(12):2137-2142.(张瀚,王秀峰,李朝晖,等.一种基于混沌系统及Henon映射的快速图像加密算法[J].计算机研究与发展,2005,42(12):2137- 2142.)
Construction method of spread-spectrum code based on multi-scroll Jerk-Chua chaos and self-coded
ZHANG Xiao-rong1,WU Cheng-mao1,LI Wen-xue2
(1.School of Electronic Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China;2.National Defense College of Engineering,PLA University of Science and Technology,Nanjing 210007,China)
In order to improve the reliability and safety of information transmission in the spread spectrum communication system,a kind of spreading code constructed by means of a combination of generalized complex multi-scroll Jerk-Chua chaos and self-coded is proposed.Firstly a new nonlinear fusion function citing by construct ideas of two-dimensional Henon transform and discrete standard mapping is produced.Then the complex multi-scroll Jerk-Chua chaos sequence is combined with the auto regressive(AR)self-coded sequence by the fusion function to generate a high quality composite random sequence as a new spreading code.Finally Matlab simulation tests show that the algorithm generating random sequence has the higher complexity and the better randomness and correlation compared with existing methods.Bit error rate has been improved in spread spectrum communication system.The transmission of information security under high security and dynamic changing conditions can be met.
complex multi-scroll Jerk-Chua chaos;auto regressive(AR)self-coded;Henon transform;discrete standard mapping;bit error rate
TN 914.14
A
10.3969/j.issn.1001-506X.2015.04.33
张晓蓉(1989-),女,硕士研究生,主要研究方向为扩频通信。E-mail:18729046967@139.com
1001-506X(2015)04-0936-06
2014- 06- 25;
2014- 08- 25;网络优先出版日期:2014- 10- 17。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141017.1606.005.html
国家自然科学基金(61073106,61136002);陕西省自然科学基金(2014JM8331,2014JQ5183,2014JM8307);陕西省教育厅自然科学资金(2013JK1129)资助课题
吴成茂(1968-),男,高级工程师,硕士研究生导师,主要研究方向为多媒体通信和图像处理。E-mail:wuchengmao123@sohu.com
李文学(1990-),男,学士,主要研究方向为国防作战指挥。E-mail:2816777806@qq.com

