零锁区激光陀螺空间异面孔系投影角测量误差分析
邓 鑫,白 波,李大琪,陈 勇
(西安飞行自动控制研究所,西安,710065)
引言
异面腔零锁区激光陀螺从原理上比二频机抖激光陀螺有更好的性能,是目前激光陀螺研究的重点方向之一[1-3]。异面腔零锁区激光陀螺的几何光路为空间异面结构,因此需要在其关键件激光陀螺腔体上加工高精度的空间异面深小孔系,作为激光的通路[4-5],如图1所示。
图1中虚线所述部分是异面腔零锁区激光陀螺腔体上的深小孔,一般孔径为Φ2mm~Φ5mm,长径比为15~25,是激光陀螺腔体上最为核心的特征。深小孔钻孔中需要对孔的位置、孔与孔的夹角进行严密控制,因此需要对加工完成的孔孔夹角进行逐一测量判断,目前的测量设备很难对腔体上的异面深小孔进行直接精密的测量,因此通常采用影像测量仪测量异面深小孔在同一基准平面上的投影角,以便描述异面深小孔的孔系加工精度。
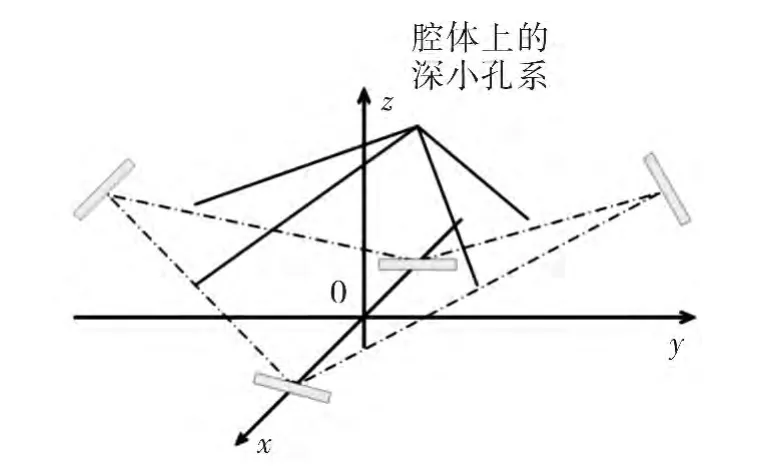
图1 零锁区激光陀螺的几何光路图Fig.1 Geometric optical path of zero-lock gyro
影像测量仪是将零件的影像按照特定比例放大后投影到圆形屏幕上,进而测量零件要素投影的几何尺寸[6]。影像测量仪在零件的二维特征测量以及共面结构的二频机抖激光陀螺腔体深小孔测量中显示了非常高的测量精度和稳定性[7-9],但对于零锁区激光陀螺异面深小孔系的投影角测量则精度和稳定性有大幅下降。
本文从倾角误差和测量采点误差两方面分析了异面腔零锁区激光陀螺腔体深小孔系投影角的理论测量误差来源,量化了测量过程中的误差对最终测量结果的影响。
1 倾角误差对正投影角的影响
假定存在任意空间角度θ,其所在平面与投影面所成二面角为β,现按照与投影面垂直的投影方向(正投影方向)将其投影到投影面上,得到角度α。则θ称之为空间角,β称之为倾角,α称之为投影角,如图2所示。

图2 空间角度的正投影关系图Fig.2 Orthographic projection relationship of space angle
若过空间角度θ的顶点A,做线段AD使其垂直于该空间角度与投影面形成的交线,即做AD⊥BC,则容易证得∠ODA则为倾角β。
角度θ、β和α的关系可通过方程表示。为书写方便,记AB=a,AC=b,BC=c,BD=c1,CD=c2,AD=h,OD=h1;∠BOD=α1,∠COD=α2。
根据各边、角之间的几何关系,可以得到以下计算方程:
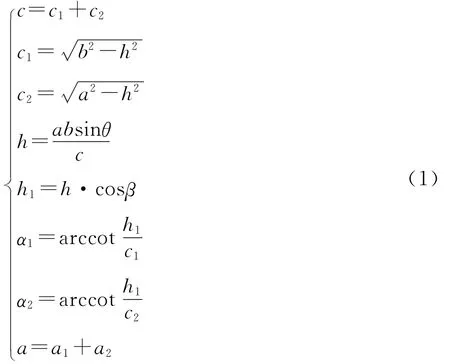

为求解倾角变化对投影角的影响,则将方程(2)进行微分求解,得到:
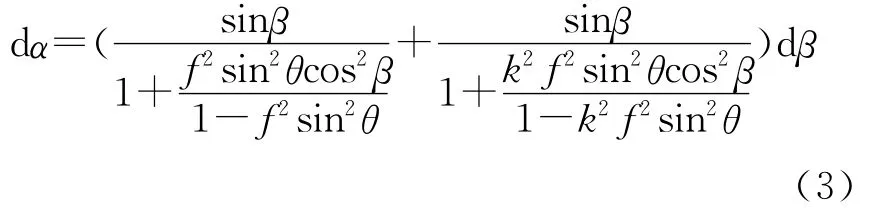
针对激光陀螺中的光路问题,一般θ=90°,k=1,(3)式可以整理为

由(4)式可以看出,当β→0时,则sinβ→0,即二维特征投影测量或共面结构的二频机抖激光陀螺腔体深小孔测量时,工作台不平或零件基准面加工误差等因素导致的倾角误差对投影角的影响非常小。而随着倾角的增加,倾角的变化(dβ)对投影角的影响逐渐增加。对于零锁区激光陀螺,由深小孔轴线组成的几何光路所在面与投影基准面的倾角通常在几度到几十度之间,因此倾角误差将会直接叠加进投影角中,对于高精度激光陀螺而言,投影角的公差一般不超过1′,因此将会对投影角测量的准确性产生非常大的影响。
为对公式进行验证,采用三维建模软件UG进行模拟仿真。建立一个90°的空间角,在不同倾角的投影面上分别测量投影角,投影角误差的仿真结果如表1所示。
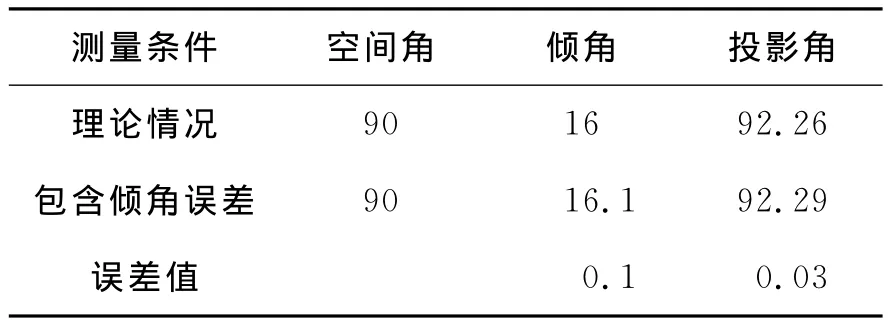
表1 倾角误差对投影角的影响 (°)Table 1 Influence of inclination error on projective angl
由表1可以看出,仿真结果与理论计算结果完全吻合。同时,当倾角误差达到0.1°时,倾角误差所导致的投影角误差已经达到0.03°,即超出了1′的公差范围。因此工作台不平或零件基准面加工误差等因素导致的倾角误差对投影角的影响非常显著,在高精度零锁区激光陀螺加工和测量中必须严格控制。
2 采点误差对投影角的影响
影像测量仪的测量原理是通过影响探测系统获取高质量、高可靠性的工件图像,并将图像转变成为数字信号,后由影像测量软件利用测量算法进行测量处理获得测量点[6]。将测量点按照最小二乘拟合的方法得到工件轮廓和所需尺寸。
因此在图像获取、图像转换、图像预处理、边缘提取过程中都不可避免的存在测量误差,在此将其统称为采点误差[10-11]。尤其在透光类的玻璃零件的孔轮廓测量中,工件图像边缘模糊问题严重,导致采点误差较大。同时,深小孔实际加工中的表面粗糙度和波纹度都会导致所测深小孔轴线与其实际轴线有偏差,采点误差导致的深小孔轴线测量误差如图3所示。
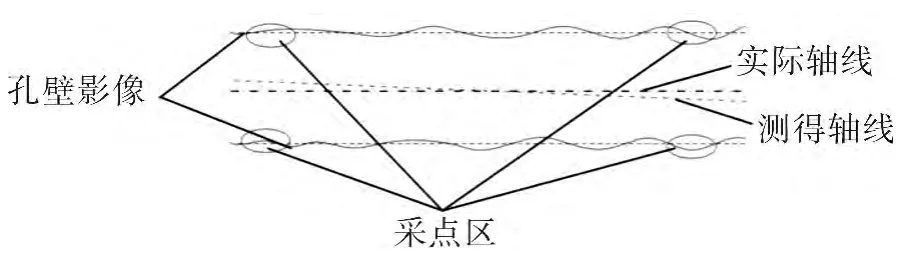
图3 采点误差导致的深小孔轴线测量误差Fig.3 Measurement error of deep hole axis causing by errors on measuring point
采点误差取决于影像测量仪的技术水平和硬脆玻璃零件深小孔加工的技术水平,在目前技术水平下很难提升。尤其是在零锁区激光陀螺的空间异面孔系的测量中,在每个采样点处影像测量仪的CCD镜头都需要重新对准焦距。并且由于是空间孔系,理论上影像测量仪的CCD镜头对焦后只有一点与所设焦距吻合,采样区域内的其他点会因为对焦不准导致孔壁边缘模糊,因此使得零锁区激光陀螺的空间异面孔系测量比平面二维测量或共面结构的二频机抖激光陀螺腔体深小孔测量的采点误差要大很多。同时 “超大”误差出现的概率也会增加。
由于采点误差具有随机性,因此增加采点数可以有效降低采点误差的影响。同时,影像测量仪的数据拟合采用最小二乘拟合的算法,增加采点数也会降低误差对整体结果的影响。假定在全长为20mm的测量范围内,均布点1至点10共计10个采样区域。在某一区域的测量中出现0.002mm的“超大”采点误差时,采点误差对最小二乘法拟合出的直线的角度影响如表2所示。

表2 0.002mm“超大”采点误差导致直线角度的偏差 (″)Table 2 Straightness error produced by 0.002 mm “super”measuring point error
从表2可以看出,测量一条直线的采样点由2个增至10个时,采用最小二乘拟合时的采样误差对角度的影响降低至原来的一半。但2个点增至3个采样点时,误差对直线角度的影响没有降低,并且会由于中间采样点位置选取的不同,误差对直线角度的影响有可能比2个测量段时角度偏差更大。
表2中给出的分析结果是只有一个采点误差的影响。在实际测量过程中,有多个测量点存在采点误差,并且随着采点数的增加,采点误差的差异性也会增加。然而,由于采点误差是随机分布的,采点误差的影响会一定程度的相互抵消。测量中某个采样点处出现“超大”采点误差时,则如表2所示,增加采点数会降低“超大”采点误差对角度测量结果的影响。
3 结论
1)本文分析了采用影像测量仪测量零锁区激光陀螺深小孔时测量误差的主要来源。并提出了控制测量误差的方法。对于工作台不平或工件基准面加工误差导致的倾角误差,给出了倾角误差对于投影角误差影响的计算公式,并采用UG软件进行了仿真验证,公式计算结果与仿真结果高度吻合。分析了采点误差的来源,并按照影像测量仪所采用的最小二乘拟合的计算方法,分析了采点误差对轴线角度的影响。并提出增加采样点,会降低“超大”采点误差对角度测量结果的影响。
2)在零锁区激光陀螺的实际加工中,定期对影像测量仪的工作台与CCD镜头的垂直度进行校验,提高基准面的加工精度,同时将空间异面孔系的测量采样区域由原来的4处增加至20处。采用以上方法,零锁区激光陀螺的异面孔系夹角测量得到改善,孔系角度测量的重复性可稳定在5″之内,能满足零锁区激光陀螺的研发需要。
[1] Martin G J,Gillespie S C,Volk C H.The Litton 11cm Triaxial Zero-lock Gyro[J].IEEE,1996(4):22-26.
[2] Wang Fei, Wang Zhiguo,Long Xingwu,Cavity Length Sensitivity in Four-mode Differential Laser Gyro[J].Infrared and Laser Engineering,2012,41(11):3097-3101.王飞,汪之国,龙兴武.四频差动激光陀螺腔长敏感性的 研究[J].红 外与激光工 程,2012,41(11):3097-3101.
[3] Chow W W,Sanders V E,Schleich W,et al.The laser gyro[J].Reviews of Modern Physics,1985,57(1):61-104.
[4] Jiang Yanan.Ring laser gyro[M].Beijing:Press of Tsing Hua University,1995:108-128.姜亚南.环形激光陀螺[M].北京:清华大学出版社,1995:108-128.
[5] Zhao Xueya,XiaYuanqin,Chen Deying.Frequencybiasing technique of Laser gyro[J].Laser & Optronics Progress,2005,42(8):50-53.赵雪亚,夏元钦,陈德应.激光陀螺的偏频技术[J].激光与光电子学进展,2005,42(8):50-53.
[6] Wang Weinong,Xu Yihua.Video measuring machine technology[M].Beijing:Press of China Commerce,2010:114-146.王为农,徐一华.影像测量仪技术基础[M].北京:中国商业出版社,2010:114-146.
[7] Yue Xiafeng,Zhao Min,Luan Baojian.Application of computer vision in detecting system of engine's surface defects[J].Computer Automated Measurement & Control,2005,13(6):516-518.岳晓峰,赵敏,栾宝剑,等.计算机视觉技术在发动机缺陷检测系统中的应用[J].计算机测量与控制,2005,13(6):516-518.
[8] Zou Huadong,Zhu Liangrong,Tao Wenyong.Precise calibration methods development and ITS'application on vision measuring system[J].Computer Measurement & Control,2010,18(9):2057-2059.邹华东,祝良荣,陶文勇.影像测量系统的精密校正方法研究及其应用[J].计算机测量与控制,2010,18(9):2057-2059.
[9] sChen Manlong.Vertical Projection measuring method for male thread and ITS'application analysis[J].Laser Technology,2012,36(6):794-797.陈曼龙.外螺纹垂直投影测量法及应用分析[J].激光技术.2012,36(6):794-797.
[10]Wang Xiaozhang,Chen Zhijun,Li Jianfeng.Research on testing errors of image measuring instrument[J].Machine Tool & Hydraulics,2009,37(11):118-119.王小章,陈志军,李剑锋.影像测量仪的测量误差研究[J].机床与液压,2009,37(11):118-119.
[11]Chen Zhijun,Wang Xiazhang,Li Jianfeng.Analysis and calculation of the optic imaging error of imagine measuring instrument[J].Science of Surveying and Mapping,2009,4(7):164-165.陈志军,王小章,李剑锋.影像测量仪的光学成像误差分析及计算[J].测绘科学,2009,4(7):164-165.

