浅谈大学物理实验中数学知识的应用

王红利　杨建伟

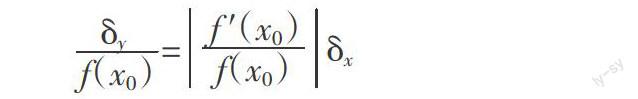
[摘 要]大学物理实验是对高等理工科学生实验能力和科学研究思维培养的重要课程，也是各专业后继实验课程学习的重要基础，研究并提高我国大学物理实验教学水平显得非常重要。数学知识对于大学物理实验中做好误差估计、数据处理以及近似替代等方面起着举足轻重的作用。将理论知识与实际操作结合起来，以提高学生的实验能力和研究思维水平。

[关键词]大学物理实验 数学知识 应用

[中图分类号] O45 [文献标识码] A [文章编号] 2095-3437（2015）10-0112-02

一、引言

物理作为一门以数学为基础的学科，与数学的结合相当紧密，其发展依赖于数学理论、数学思想和数学方法，而且物理中大量地应用到了数学知识和数学方法。几乎所有物理实验中的误差估计、数据处理以及近似替代等都离不开数学知识，因此数学是做好物理实验写好实验报告的关键所在。虽然目前国内很多理工科类高校在大学物理实验课程学习之前，已经开设相应的高等数学课程，但由于学生对所学高等数学知识的整体把握度还不够，甚至于对部分内容的掌握还相对生疏，从而不知道在大学物理实验中如何去应用所学的数学知识，进而导致实验数据测量误差大、数据处理不合理、分析计算过程复杂等诸多问题。因此，如何在大学物理实验中正确和熟练应用数学知识就成为做好大学物理实验写好实验报告的关键。笔者根据自身多年的教学体会，结合一些具体实例分析了数学知识在大学物理实验中的应用。

二、微分在误差估计中的应用

在大学物理实验教学中，一开始就要讲解误差的基本知识和近似计算方法，这其中包括如何运用微分来计算间接测量误差和相对误差。我们知道，利用任何测量工具和仪器进行测量时，误差总是在所难免。假设x是由测量得到，实际测得的只是x的某一近似值x0，因此由x0计算得到的量y0=f（x0）也只是被测量y=f（x）的某一近似值。如果已知测量值x0的误差限为δx[4]（其与所使用的测量工具的精度有关），于是绝对误差记为△x=x0-x，且△x？燮δx，则当δx很小（测量工具较精密）时，由微分的意义知被测量误差的绝对值

△y=f（x）-f（x0）≈f ′（x0）△x？燮f ′（x0）δx，

于是可求得相对误差限

三、最佳最小二乘解在实验数据处理中的应用

在许多大学物理实验中，如电位差计测电动势、金属丝的线膨胀系数的测量等，我们经常需要根据实验测得一系列数据，例如，n个数组（xi，yi）（i=1，2，…，n）去寻找自变量x和因变量y之间最能反映出给定数据之间的最佳关系，这就是所谓的曲线拟合问题。要找出不同变量之间的关系。我们可以通过传统的处理方法，如图解、目测的方法来达到目的。然而，在有些情形下，由于误差的介入，使得到的结果往往并不是最佳的近似，甚至还会得到非常错误的结论。而最小二乘法是一种行之有效的数学方法，用此法拟合同一组实验数据时，不论谁来处理，只要数据处理过程没有错误，都会得到一致的结果。

我们可以用最佳最小二乘解的知识，很容易解决在大学物理实验取得测量数据之后遇到的寻找经验公式问题，即曲线拟合问题。这种方法与传统的最小二乘法相比，具有形式简单、计算简便、过程简约的特点。事实上这种通过求解最佳最小二乘法的方法与传统的最小二乘法可以证明是等价的。高等数学中关于最小二乘解的定义[5]是：设A∈Cm×n，b∈Cm，若存在u∈Cm，使得对？坌x∈Cn，都有‖Au-b‖2？燮‖Ax-b‖2，则称是u矛盾方程组（即无解）Ax=b的一个最小二乘解。注意这里的‖·‖2表示通常的欧几里得范数。又设x0是Ax=b的最小二乘解，若对于Ax=b的每一个最小二乘解u，都有‖x0‖2？燮‖u‖2，则称x0是最佳的最小二乘解（最佳逼近解）。

事实上，我们知道x0是唯一的并且x0=A+b，其中A+是系数矩阵A的加号广义逆。而且还可以得到误差估计为‖δ‖=‖Ax0-b‖2.

例如，我们测得一组实验数据：（1，3），（2，5），（3，6），（4，7），从数据点的走向上看这些点非常接近一条直线，希望使用直线y=m+kx来拟合上述数据点。将实验数据代入y=m+kx可得矛盾方程组Ax=b，即

1 11 21 31 4mk=3567.

显然系数矩阵A是列满秩的，所以A的左逆（ATA）-1AT就是A的加号广义逆A+，于是

所以最佳拟合直线为y=2+1.3x，其误差为

‖δ‖2 =‖Ax0-b‖2 =0.5477.

事实上，这种方法可以用来拟合数据点近似满足的其他曲线，譬如抛物线、椭圆等。

四、等价无穷小在大学物理实验中的应用

在大学物理实验中，很多地方都会用到等价无穷小的高等数学知识。等价无穷小的定义为：设当x→0时，f（x）和g（x）都是无穷小量，，则称f与g是当x→0时的等价无穷小，记作f（x）～g（x）（x→0）。如在杨氏模量的测量这个实验中，平面镜转过的角度为θ，在利用光杆法测量长度变化量时，就用到了当θ很小时用其来近似替代tanθ，这样就使问题在不牺牲误差限的前提下大大简化。同样，在莫尔条纹的观测和应用这个实验中，也用到了当θ很小时用其来近似替代2sin，这里的θ表示两个等距光栅之间的夹角。此外在全息光栅、用单摆测量重力加速度、双棱镜干涉测量单色光波长等许多大学物理实验中也有相同的处理方法。

五、数学软件在大学物理中的应用

我们知道，Maple、Matlab、Mathematica和Mathcad都是非常有名的数学软件，它们集成了数值计算、符号计算、图形界面、高级语言编程以及动画制作等强大功能。随着信息技术的发展，这些数学软件也逐步被应用到大学物理实验的教学中。例如，在密立根油滴实验中，我们可以根据该实验中的相关公式和各参变量数值，借助Mathematica软件中的Plot命令做出油滴匀速下降的时间与油滴所带电量、油滴电量误差以及基本电荷误差等的曲线图，这样我们就很容易从做出的这些曲线图中很直观的看出油滴匀速下降所需的时间越短，油滴所带的电量就越多、油滴电量的误差就越大；还可以看出油滴匀速下降的时间无限接近某一常数时，基本电荷的误差也越小。又如，在普朗克常数测量试验中，我们运用Matlab软件对所取得的物理实验数据处理进行模拟，这样可以极大程度地避免繁杂的数学运算过程，并增加数据处理的准确性。

数学软件在物理实验教学中的使用将计算机应用与大学物理实验相融合，既可以使实验内容以图文并茂的形式展示，有助于调动学生的积极性；也可以帮助学生深刻理解物理场景，拓宽学生视野，激发学生学习的兴趣。

八、结束语

本文分析了大学物理实验中数学知识的重要性，通过一些实例分析了微分、最佳最小二乘解、等价无穷小以及数学软件等数学知识在大学物理实验中的具体应用，但事实上大学物理实验中所涉及的数学知识远远不止这些，在此我们不再赘述。笔者的意图在于通过分析大学物理实验中数学知识的应用，引起广大物理学习者的注意，要想做好物理实验，写好实验报告，就必须先学好数学，同时也通过本文起到抛砖引玉的作用。

[ 参 考 文 献 ]

[1] 单雯雯，袁保合.大学物理实验[M].郑州：河南科学技术出版社，2012.

[2] 王燕红，宋玲.大学物理实验[M].郑州：黄河水利出版社，2009.

[3] 赵光强，申莉华，李玉琮.大学物理实验教程[M].北京：北京邮电大学出版社，2010.

[4] 同济大学数学系.高等数学（第六版）[M].北京：高等教育出版社，2007.

[5] 杨明，刘先忠.矩阵论[M].武汉：华中科技大学出版社，2004.

[责任编辑：张 雷]