课程测评系统的试题智能组装方法

鲍宇 王凯馨 张艳群

摘要：分析课程测试系统试题的题干和问题组成的基本特征，提出利用题干和问题的智能匹配策略，通过模块化组装的形式与调整试题可变参数来生成问题和题干并创建试题，最终依据题型与知识点章节的划分来抽取和生成测评内容。

关键词：测评系统；背包算法；智能组装方法

0、引言

随着互联网和信息科学技术的迅猛发展，网络技术的应用领域不断拓宽，网络自主学习与课堂教学的结合已成为当代教学手段改革的主要方式。其中，利用网络信息技术协助完成自主学习过程成为该类教育技术革新的亮点之一。通过自主学习平台中的自主测评来完成自主在线测评，以及系统自带的自动阅卷功能，使得被评测者能够随时随地地进行自我检测，这无疑方便和促进了使用者的学习。

经研究发现，目前学习网站测评系统还存在尚未完善的地方。例如测评系统形成试卷的方式固定，采用的是从同一题库中抽取现有试题组成试卷的方法。这种方法产生的试题类别与数量有限，不易解决试题抽取重复率高的问题。

1、选题与组卷算法没汁

1.1组卷与背包问题

组卷就是根据要求从试题库中选择试题组成—份符合要求的试卷。通过研究试卷的结构，发现任何一份试卷都可以分成以下3个部分来描述：①试卷的总体结构，用来描述试卷的整体信息，包括总体难度、试卷题型、试题数目等信息；②试卷单元，用来表示试卷所包含的题型，即每一题型为一试卷单元，包括题型、试题数、知识点章节分布，分数等信息；③试卷单元所包含的若干小题，用来描述试卷单元中每个小题的详细信息，包括每个小题的题型、分数、所属知识点章节。这样，组卷过程实际上就是根据一定的约束条件，从试题库中抽取若干小题组成一个个试卷单元，再由这若干个试卷单元构成一张完整试卷。若将一个试卷单元作为一个背包，背包所能装入的试题数为背包容量，试题小包中的试题为所有的物品，则该问题的求解就转变为背包问题的求解。每一试卷单元依据所属题型匹配不同试题小包，得到每个试卷单元后，再将整张试卷作为一个大的背包，将所得到的试卷单元装入背包，直到装满为止，从而就得到了整个试卷的解。至此，组卷实际上就转化为了背包问题。

背包问题是一个非常经典的优化问题背包问题约束如下：设有一个背包，可以放入重量为S。现有，n件物品，重量分别为Sl，S2…Sn且均为正数，从这n件物品中选择若干物品放入此背包，使得放入总重量恰好为S。

与解决背包问题类似，可以利用“回溯”的设计思想来解决此组卷问题。针对一个试卷单元，设其所要求包含试题数为S，从试题库中选取小题，然后将所选小题i放入试卷单元中，如果已经选取的试题数i小于s，则继续选取第1+1道题放人试卷单元中，直到试卷单元中的试题数为S为止。如果剩余试题中找不到合适的小题放人试卷单元，则说明刚刚装入试卷单元的小题“不合适”，应将它“弃置一边”，继续选择“它之后”的小题。如此重复，直到求得满足要求的解或者无解为止，这样得到一个试卷单元。同理，将所得到的若干试卷单元依次装入试卷，直到得到一张完整的符合要求的试卷。

1.2基于背包问题的组卷算法设计

将组卷问题转化为背包问题后，则组卷问题就是依据一定的限制条件，合理地选择试题“装入”试卷中。对此，首先要划分可装入的试题。分析试卷结构可知，一张完整试卷由若干题型组成，而每一题型又包含若干不同知识点章节的小题。所以，先依据不同的题型，将一整张试卷划分为i个试卷单元Item（i），再依据所属不同知识点章节，将每个试卷单元划分为i部分，即对于每个试卷单元i包含j（j>=0）道题，分别来自于j个知识点章节。在选取j道试题填充试卷单元Item（i）时，由于是采用随机数发生器来随机地选取知识点章节，就有可能出现某些知识点在同一或不同试卷中重复出现，造成试卷知识点章节横向纵向分布不均匀的问题，所以这里为属于同一知识点章节的任意类型的试题设置相同的频率参数ε，ε在这里代表该知识点章节试题出现的频率。在进行试题抽取前，所有题库中试题的ε初始化为相同的值，如设置为l/μ，设某一知识点章节的试题被抽取次数为κ，则抽取κ次后该知识点章节的ε更新为：

εj=1+k/μ+k（1）

其余知识点章节的ε随着更新为：

εm=1/μ+k（2）

随抽取次数κ的增加，εj会最终大于εm，即k越大，εj大于εm的程度越大，在题库中相对出现频率越大。那么在随后的抽取试题的过程中，会优先选择ε小的知识点装入试卷单元Item（i），这样可以使试卷结构分布更均匀，避免同一或不同试卷知识点分布不均的现象。

综上，将每道试题记为Item（i，j，εj），i表示题目类型，j表示所属知识点章节，εj表示该知识点章节试题出现的频率。则基于背包问题的组卷问题就可看做，从已有的试题小包中抽取试题Item（ij，εj），将试卷单元Item（i）装满，再由Item（i）组成一张完整试卷的过程，试卷填充结构如表l所示。

根据上述描述，设计基于背包问题的组卷算法如下：

算法l：基于背包问题的组卷算法

void getSolutions（试卷单元，试题小包）{

k-random（）xlOOOO%size； //size为试题小包中的物品个数

WHILE（试卷单元朱装满且有试题小包不空）{

IF（试题小包中的第κ个题可取）

将κ试题放入试卷单元内；

k=random（）×lOOOO%size；//继续考察试题小包中的下一个题

}

IF（试卷背包恰好装满）{求得一组解；}

退出试卷单元中的最后一道题k；

κ=random（）×lOOOO%size；//继续考察试题小包中的下一道题

}

2、试题组装及智能组装策略

2.1试题组装

解决了组卷问题后，接下来我们要讨论如何得到大量可选试题。若采用从固定题库中抽题的方法，那么可以使用的试题数目非常有限，且容易重复，所以我们提出采用动态组装试题形成试题的方法来解决这个问题。仔细观察某些试题就会发现，一道试题从语法结构上能划分为若干部分，可以看做是多个前提、问题约束及问题的集合，即{前提1，前提2，……}、{问题约束1，问题约束2，……}，{问题l，问题2，……}，也就是说每道题都由若干题干搭配组合而成。对于该类试题，通过几个题干集合的排列组合，形成不同的试题，若将每一集合分别拓展开来，即由设计者预先定义好每一集合所包含的若干元素，按照一些组题策略，通过几个子集中元素的组合搭配即可形成数量可观的试题，很好地解决了传统固定题库抽题所带来的问题。对于试题组装，本文作如下设置：

设题干小包Bagi（i=0，1，2，3）：

Bagl中元素为（Prebagl，Prebag2，Prebag3....），为前提小包Prebag，每一Prebagi内容为一给定的大知识点范畴（如树、图、数组等），Prebagi中元素为ai；

Bag2中元素为（Tipbagl，Tipbag2，Tipbag3...），为问题约束小包Tipbag，内容涉及具体问题约束，如相关算法、所提供的某些具体条件等；每一Tipbag包含若干可与 Prebagi中某一元素搭配的元素bi；

Bag3中元素为（Quebagl，Quebag2，Quebag3....），为问题小包Qucbag，内容为所提出的问题，如“求解……A.B、C”等；每一Quebag包含若干可与Tipbag/中某一元素搭配的元素ci。

对于包含参数的试题来说，还可以通过使用随机数发生器，对题干所包含参数进行随机修改，形成新的题干元素，再按照试题组装算法进行试题组装。在预先设置题干小包Bagi时，对其中元素所包含的参数进行初始化，在形成试题过程中，再随机生成数字，代替原有参数，这样不仅增加了试题的数量，还可减少试题的重复性；也可将作为问题的题干位置设为参数，进行随机化处理。

2.2组装策略

依据题干的位置不同，可将组装策略分为两类：题干视为参数型组装策略、题干位置固定型组装策略。第一种类型中，将题于视为参数，并随机选取问题题干的位置，如问题题干放到句末，或是将包含已知条件的题干作为问题（可作选择题、填空题）；第二种类型为默认问题题干在最后给出。对于不同的类型，有不同的组装策略，先给出两类组装策略的通用策略：

（1）题干组装策略。在组题过程中，对每个上一层的题干小包中的元素，选取可搭配的题干小包。又每一元素有可能只与某些小包中的元素可搭配。所以，当上一层小包中元素为空，或找不到可搭配的下一层小包时，就要采用回溯法返回到上一步，开始新一轮的搜索匹配。

（2）参数随机策略。如在选定Bagl中的Prebag后，Bag2中与其搭配的Tipbag不一定只有一个，这时就需要随机选取一个Tipbag，对于接下来的小包或元素选取也采用同样的随机方法，以确保组题步骤的连续性和随机性，特别是对于有参数题干中参数的随机生成。这要求使用一个运算速度快，分布均匀的随机数发生器。

（3）语法语义判断策略。由于组题完全由系统进行，在组装出的试题中有可能存在误差，有些可组装试题不一定符合语法规则，或在答案链表中搜索不到可匹配答案，这要求丢弃该类试题，继续进行其他的试题组装。

（4）题型选择策略。生成一道完整试题后，若给出可选答案，即为选择题；若无可选答案，则为综合题；若题干中含有空缺部分，则为填空题。

以上策略对于两种类型的组装方法都适用，接下来给出仅适用于题干视为参数型的组装策略：①题干参数化策略：在这种类型中，将题干的位置视为参数，即可以随机生成题干位置，一个题干既可作为问题约束部分，也可作为提出问题部分。例如将来自3个小包中的题干元素ai，bi，ci视为参数，既可以由ai>bi>ci连接方式形成一道题，也可由ai>ci>bi的连接方式形成一道题。这里将题干的位置参数化，并设为随机。②问题题干截取策略：由题干组装形成一完整试题后，随机截取题干所给已知条件，并将所挖部分作为试题答案，以此生成选择或填空题。

最后给出仅适用题干位置固定型的组装策略：题干选择策略，即当Bagi题干小包的元素不为空，并且从中可找到与Bagi-l小包的元素搭配的元素时，则选取该元素；依照Prebag->Tipbag->Quebag的次序进行题干选取，直到得到足以组装成一道完整试题的若干题干，将其依序连接成一道完整试题。

2.3算法实现

在组装试题时，分别从不同的Bagi中随机选取元素小包，在不同的元素小包中随机选取题干元素，依次进行人栈。之后依次取出入栈的题干元素，按顺序进行链接，形成一道完整试题，然后进行语义语法分析，看是否为可用试题。若经过检验，则将试题放入题库，然后对所得题干元素进行排列组合，选出符合语法规则的试题放入题库（不包括之前得到的依序组装的试题），以此实现组装策略中的题干视为参数型的试题组装；若没有经过检验，所得试题不符合语法规则，则将栈顶的题干元素出栈，选择其他的题干元素入栈，如此反复，得到试题库。具体算法实现步骤如下：

算法2：试题组装算法

Stepl：从Bagl中随机选择任一Prebagx；若为空，则组题过程结束；

Stcp2：若Prebagx非空，则从Prebagx中随机选取元素am，将am入栈；若为空，返回Stepl；

Step3：从Bag2中搜寻可与am搭配的Tipbag小包，从搜寻结果中随机选择一Tipbagy；若为空，am出栈，返回Stcp2；

Step4：从Tipbagy巾随机选择元素bn，将bn人栈，若为空，返回Step3；

Step5：从Bag3 ff I搜寻可与bn搭配的Quebag小包，从搜寻结果中随机选择一Quebagz；若为空，6n出栈，返回Step4；

Step6：从Quebagz中随机选择元素ci，将Ci入栈，若为空，返同Step5；

Step7：获取栈中元素，根据入栈顺序连接元素am->bn->ci，进行语义分析，若符合语法规则，则将该题目中所含参数进行随机具体化，并将其作为综合题存入题库；

注：由于整个组装试题过程由程序来完成，试题是由几个题干元素搭配而成，在连接成句时或多或少会存在语句不通，语义不搭的情况，所以连接后进行语义语法分析是必要的。只有符合语法语义规则，且符合问题逻辑的试题才可以作为可用试题存入题库。

Step8：再将所得题干元素am，bn，ci视为参数，进行随机排列组合，对所得每一种结果（除Step7中所得试题）进行语义分析，若通过检验，则随机挖取题干元素所给已知条件，并将所挖部分作为试题答案，以此生成选择或填空题存入题库；出栈ci，返同Step6。

3、应用举例

以数据结构中图及树的有关知识点为例，进行题干小包划分，并实现题干组装。

首先设置题干小包Bag/（这里取/=3）：对于Bagl，选取一元素Prebagl小包，Prebagl中元素为以“图”及“树”为范畴的知识点，记为ai；对于Bag2，其中可选择元素为Tipbagl. Tipbag2，Tipbag3，Tipbag4，每个Tipbagi中包含若干可选元素，每一Tipbag中元素记为bij；对于Bag3，可选元素为Quebagl，Quebag2，Quebag3，每一Quebag/中含有可选元素，每一 Quebag中元素记为cij。

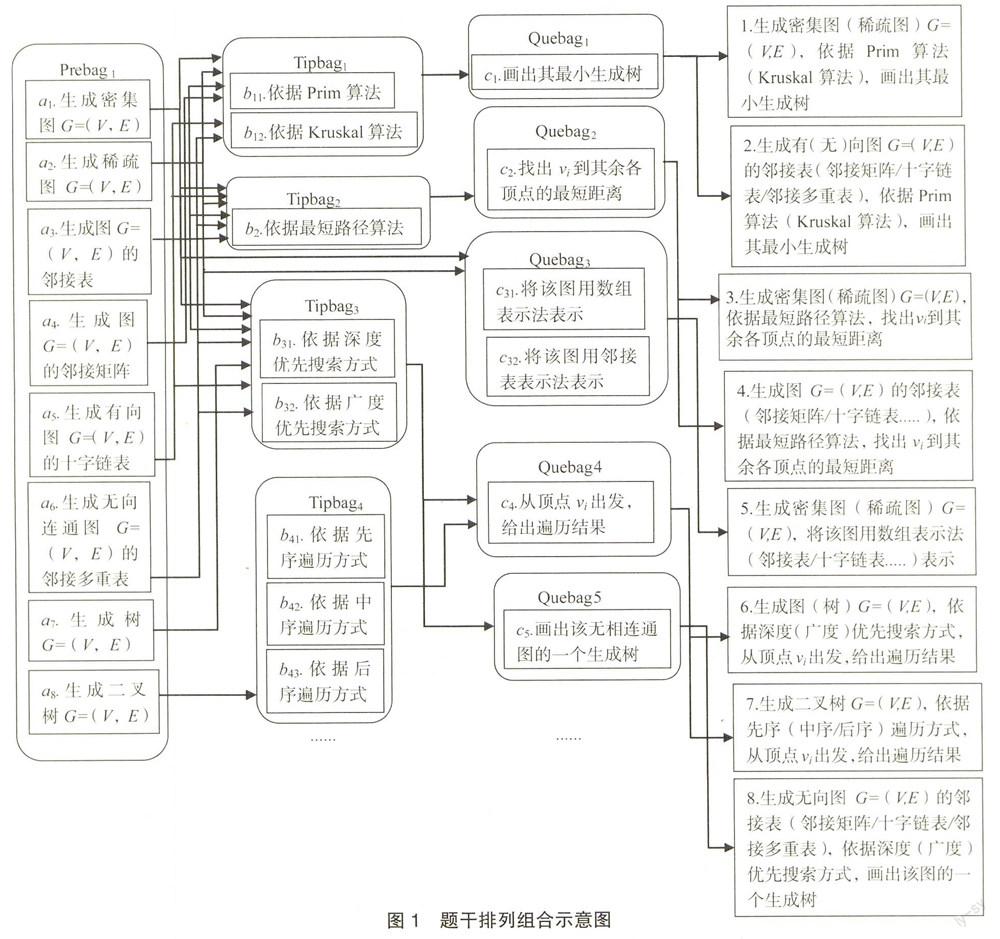
依据以上设置进行一部分的题干小包初始化，部分题干小包排列组合结构如图l所示。

下面是一道试题的具体生成过程：

（1）随机在Bagl中选取Prebag小包，获得Prebagl小包，随机取其中的元素，得到a3，并将其入栈；

（2）随机在Bag2中选取可与元素a3搭配的Tipbag小包，获得Tipbag2小包，随机取其中的元素，得到62，并将其入栈；

（3）随机在Bag3中选取可与冗素62搭配的Quebag小包，获得Quebag2小包，随机取其中的元素，得到c2；

（4）将元素a3，b2，c2出栈，依据人栈顺序，将所得元素依次连接，组成一道试题，然后进行试题语义语法分析，若符合语法规则，则使用随机数发生器具体化其中的参数图G（V.E）及结点vi；

（5）将试题作为综合题存入题库。至此，通过依次在Prcbagl，Tipbag2，Quebag2小包中分别选取题十元素a3，b2，c2，再将这些元素依次连接成句，并具体化其中的参数，进而形成“已知图Gl=（V，E）的邻接表，依据最短路径算法，找出vl到其余各顶点的最短距离”这道试题。

对图1中题干排列组合进行分析，可得题干组装试题为：

al～a6->bll～b12->cl；

a1～a6->b2->c2：

al～a2->c31～c32：

al～a7->b31～b32->c4；

a6->b31～b32->c5：

a8->b41～b43->c4：

总共可组合形成试题数：N=6×2×1+6×1×1+2×2+7×2×1+1×2×1+1×3×1=41道。这里只给定了某些题干小包的一部分元素，并且组装过程未包括题干视为参数的组装过程。可以想象，如果完整地将数据结构的所有知识点进行题干划分，按照本文所述题干组装方法进行试题组装，将会动态得到数量十分可观的试题。并且，在这些试题中，抽取出现重复的概率很小；除此之外，由于产生的试题难度相差不会过大，可以同时提高评测的随机性和公平性。

4、结语

智能出卷测评系统的实现打破了传统从固定题库中抽取试题组成试卷的出卷方式，在增加试题数量的同时，也使得试题重复的概率极小，使得测评系统出题更加智能化，试卷组成更加多样化，服务学生更加个性化。我们提出的测评系统仍存在不完善的地方，比如设计者分析搭配关系需要很大的工作量；在组装试题过程中会出现不符合语法语义的试题等。

总之，此种智能测评系统不仅可以极大地方便和丰富学生的试题训练，还可将其应用在服务于其他群体的网站测评系统中，从而为大众提供更高质量的在线测评服务。