几何证明选讲、坐标系与参数方程和不等式选讲命题规律与备考策略

高慧明

本专题包括：几何证明选讲 、坐标系与参数方程和不等式选讲.

几何证明选讲主要内容有：相似三角形的定义与性质、平行截割定理、直角三角形射影定理、圆周角定理、圆的切线判定定理与性质定理、相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.

坐标系与参数方程主要内容有：坐标系、极坐标的基本概念、极坐标和直角坐标的互化.简单图形（如过极点的直线、过极点或圆心在极点的圆）表示的极坐标方程、参数方程的基本概念、直线、圆和圆锥曲线的参数方程.

不等式选讲主要内容有：（1）含绝对值不等式;（2）通过一些简单问题了解证明不等式的基本方法：比较法、综合法、分析法.

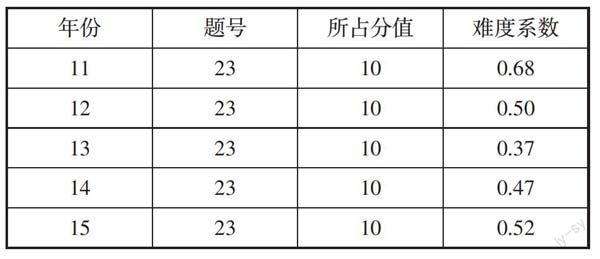
本专题共有10个知识点，5年来全国高考试题先后均涉及到10个知识点，高考覆盖率为100%.本专题在高考中是选做题中的一个解答题，总分10分，分值比重为6.66%，试题平均难度为0.44.

在能力考查方面，主要考查：推理论证能力4%.运算求解能力3%

本专题的中高频考点及五年高考试题中出现的频数有：圆内接四边形的性质定理与判定定理（频数3），极坐标和直角坐标的互化（频数3），含绝对值不等式（频数5）.

根据上述分析可以看出，高考命题在本篇中特别突出了几何证明选讲中圆的相关定理的运用考察，坐标系与参数方程中极坐标和直角坐标的互化、参数方程与一般方程的互化的考察，不等式选讲中含绝对值不等式的相关问题的考察.

从知识范围来看，本篇是高考选做题，主要是几何证明选讲 、坐标系与参数方程、不等式选讲三专题中选做一题.此内容是以解答题的形式出现，分值10分，难度不大.

从能力要求来看，本篇是高考命题的一个特点，考生根据自己的学情选做，但三专题均始终是考查推理论证能力，运算求解能力，所占比重约为7%.

从题型分布来看，三专题各为一个解答题，分值都是10分.考生选做一题.

从试题难度来看，平均难度约为0.45，属于中档题.

上述考查宗旨和特点已呈现出持续稳定的态势，必然会影响到今后的命题.

第一单元   几何证明选讲

【考情分析】几何证明选讲近五年的高考考查情况是：

基本属于中档题.

【考点聚焦】

几何证明选讲主要内容有：（1）理解相似三角形的定义与性质，了解平行截割定理.（2）会证明和应用以下定理：①直角三角形射影定理;②圆周角定理;③圆的切线判定定理与性质定理;④相交弦定理;⑤圆内接四边形的性质定理与判定定理;⑥切割线定理.

【经典解析】

考点1：平行截割定理

例1. 在梯形ABCD中，点E，F分别在腰AB，CD上，EF∥AD，AE∶EB=m∶n.

求证：（m+n）EF=mBC+nAD.你能由此推导出梯形的中位线公式吗？

【思维生长点】由题目可获得的主要信息及解题思路：.

【收获与点评】本题旨在考查考生对平行线分线段成比列定理的掌握情况，考察考生的综合分析问题能力，属于中档题.

考点2：圆的相关定理和性质

例2. 如图2，已知⊙A、⊙B都经过点C，BC是⊙A的切线，⊙B交AB于点D，连结CD并延长交⊙A于点E，连结AE.

（1）求证：AE⊥AB;

（2）求证：DE·DC=2AD·DB;

（3）如果DE·DC=8，AE=3，求BC的长.

【思维生长点】由题目可获得的主要信息及解题思路：

【收获与点评】本题旨在考查考生对圆的切线的判定定理及性质定理及弦切角定理及其推论、相交弦定理、割线定理、切割线定理等问题的掌握情况，在证明一些带有倍数的乘积式（或比例式）时，常常需要将它转化为标准的比例式，即用具体的线段代换“倍线段”，以便进一步探寻，属于中档题.

例3. 如图所示，P是⊙O外一点，PA是切线，A为切点，割线PBC与⊙O相交于点B，C，PC=2PA，D为PC的中点，AD的延长线交⊙O于点E. 求证：

（Ⅰ）BE=EC;

（Ⅱ）AD·DE=2PB2.

【思维生长点】（Ⅰ）连接AB，AC.由题设知PA=PD，

【收获与点评】平面几何是一门研究平面内几何图形性质的基础学科.学习几何是训练思维的最好方式. 在现代，几何更成了理工科类的基础学科之一.对于考生而言，千变万化的几何图形深深的吸引着他们.考生大都认为几何比代数更具体、更形象，有一种直观的美感.本道题第一问采用分析法（要证BE=EC只需证明∠DAC=∠BAD），从而解题思路得以进行.第二问利用相交弦定理比较容易处理.

考点3：四点共圆的判定

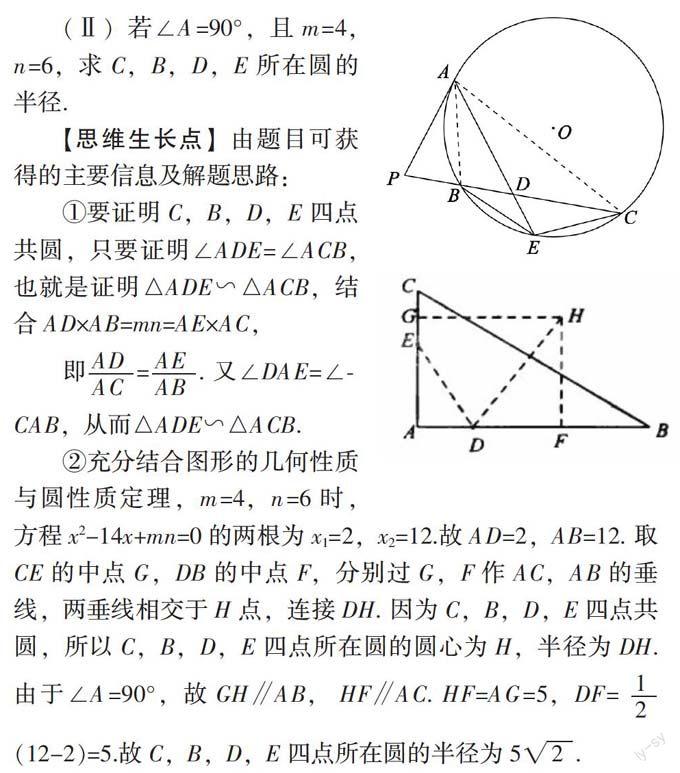
例4. D，E分别为？驻ABC的边AB，AC上的点，且不与？驻ABC的顶点重合.已知AE的长为n，AC的长为m，AD，AB的长是关于x的方程x2-14x+mn=0的两个根.

（Ⅰ）证明：C，B，D，E四点共圆;

（Ⅱ）若∠A=90°，且m=4，n=6，求C，B，D，E所在圆的半径.

【思维生长点】由题目可获得的主要信息及解题思路：

【收获与点评】本题以三角形为载体，考察了四点共圆的判定，同时还考察了圆的相关性质，是比较综合的问题，属于中档题.

【复习攻略】

本单元在高考试卷中占10分，对考生推理论证能力的要求较高，试题难度中等偏难.因此，其复习时间应有2～3课时为宜，并且配以适量的课后作业.

本单元应重点掌握的知识包括：相似三角形的定义与性质、平行截割定理、直角三角形射影定理、圆周角定理、圆的切线判定定理与性质定理、相交弦定理、圆内接四边形的性质定理与判定定理、切割线定理.

本单元复习的基本方法是：借助图形，用心观察，善于分析，手脑并用，多画图、画好图有利于建立图形元素间的联系，提高图形分析推理能力.

第二单元   坐标系与参数方程

【考情分析】坐标系与参数方程近五年的高考考查情况是：

基本属于中档题.

【考点聚焦】

坐标系与参数方程主要内容有：坐标系、极坐标的基本概念、极坐标和直角坐标的互化.简单图形（如过极点的直线、过极点或圆心在极点的圆）表示的极坐标方程、参数方程的基本概念、直线、圆和圆锥曲线的参数方程.

【经典解析】

考点1：圆的参数方程

【思维生长点】由题目可获得的主要信息及解题思路：

【收获与点评】参数重要的功能是把两个变量间的关系用一个变量来表示，引进参数能起到降维的功能，使问题简化.本道题难在转换（因为C在点D处的切线与l垂直，所以直线GD与l的斜率相同），这种转换是建立在数形结合的恰当应用上.

考点3：极坐标和直角坐标的互化

【收获与点评】本题主要从坐标和方程两个角度来考察了极坐标和直角坐标的互化，属于容易题.

【复习攻略】

本单元在高考试卷中占10分，对考生计算互化能力的要求较高，试题难度中等.因此，其复习时间应有2～3课时为宜，并且配以适量的课后作业.

本单元应重点掌握的知识包括：坐标系、极坐标的基本概念、极坐标和直角坐标的互化.简单图形（如过极点的直线、过极点或圆心在极点的圆）表示的极坐标方程、参数方程的基本概念、直线、圆和圆锥曲线的参数方程.

本单元复习的基本方法是：了解坐标系、极坐标的基本概念，充分认识坐标系的作用和意义，坐标系的思想是现代数学最重要的基本思想之一，是联系代数和几何的桥梁，充分体现了“形”与“数”二者的有机结合，也是其它几何问题、函数问题、方程问题等的基础。借助于坐标系，我们可以把几何图形用代数的形式表示出来;熟练掌握极坐标和直角坐标的互化，从而将不熟悉的问题划归为熟悉的问题加以解决;领悟参数方程的基本概念和作用，参数的选择是参数方程应用的关键;要学会比较，学会选择，数形结合，要善于将它们有机结合、互相转化.

第三单元   不等式选讲

【考情分析】不等式选讲近五年的高考考查情况是：

基本属于中档题.

【考点聚焦】

不等式选讲主要内容有：（1）含绝对值不等式;（2）通过一些简单问题了解证明不等式的基本方法：比较法、综合法、分析法.

【经典解析】

考点1：解含绝对值不等式

例1. 设函数f（x）=|x-a|+3x，其中a>0.

（Ⅰ）当a=1时，求不等式f（x）≥3x+2的解集;

（Ⅱ）若不等式f（x）≤0的解集为{x|x≤-1}，求a的值.

【思维生长点】由题目可获得的主要信息及解题思路：

①当a=1时，f（x）≥3x+2可化为|x-1|≥2.

由此可得x≥3或x≤-1.

故不等式f（x）≥3x+2的解集为{x|x≥3或x≤-1}.

②关键在于去绝对值符号的分类讨论：由f（x）≤0，得

【收获与点评】本题旨在考查考生对解含绝对值不等式的掌握情况，考察考生的分类分析问题和计算能力，属于中档题.

考点2：含绝对值函数的作图及函数图像间的关系

例2. 设函数f（x）=|2x-4|+1，

（Ⅰ）画出函数y=f（x）的图像

（Ⅱ）若不等式f（x）≤ax的解集非空，求a的取值范围.

【思维生长点】由题目可获得的主要信息及解题思路：

①要作函数y=f（x）的图像，要将原函数化简为分段函数：

【收获与点评】本题旨在考查考生作图能力，和化归的数学思想，要考生善于从函数的观点解决问题，属于中档题.

例3. 已知函数f（x）=|x-8|-|x-4|，

（1）作出函数y=f（x）的图像;

（2）解不等式|x-8|-|x-4|>2.

图像如下页.

（Ⅱ）不等式|x-8|-|x-4|>2，即f（x）>2，

由-2x+12=2得x=5.

由函数f（x）图像可知，原不等式的解集为（-∞，5）.

【收获与点评】在解题时函数、不等式、方程几者之间合理地转化，能起到化繁为简的功效. 本题考查了分类与整合的数学思想方法. 属于较简单题目.

考点3：解含绝对值不等式及恒成立问题

例4. 设函数f（x）=|x-1|+|x-a|，

（1）若a=-1，解不等式f（x）≥3;

（2）如果？坌x∈R，f（x）≥2，求a的取值范围.

【思维生长点】由题目可获得的主要信息及解题思路：

②由（2）中恒成立问题条件出发可知关键在于求f（x）的最小值;其次结合函数f（x）=|x-1|+|x-a|的在数轴上的几何意义可知f（x）的最小值为|a-1|.

从代数分析如下若a=1，f（x）=2|x-1|，不满足题设条件.

若a<1，f（x）=-2x+a+1，x≤a1-a，a

若a>1，f（x）=-2x+a+1，x≤11-a，1

所以？坌x∈R，f（x）≥2的充要条件是|a-1|≥2，从而a的取值范围为（-∞，-1]∪[3，+∞）.

【收获与点评】本题以恒成立问题为载体，考察了解含绝对值的不等式及如何求含绝对值函数的最值问题，同时还要考生善于从数、形两个角度来理解问题实质，是比较综合的问题，属于中档题.

【收获与点评】不等关系在现实生活中比比皆是， 选修4-5，不等式选讲部分是不等式、不等关系的补充，本道试题第一问，要利用一个简单的绝对值放缩.第二问利用分类讨论的思想方法解绝对值不等式.

【复习攻略】

本单元在高考试卷中占10分，对考生分类讨论分析问题的能力的要求较高，试题难度中等.因此，其复习时间应有1～2课时为宜，并且配以适量的课后作业.

本单元应重点掌握的知识包括：含绝对值不等式的相关问题，不等式证明的基本方法.

本单元复习的基本方法是：解不等式的核心问题是将不等式要同解变形，由复杂向简单转化，不等式的性质、去绝对值符号的分类讨论是同解变形的理论依据，方程的根、函数的图像和性质都会给不等式的求解提供帮助，要善于将它们有机结合、互相转化.

（作者单位：北京市第十二中学）

责任编校 徐国坚