函数最值几种解法在高中数学教学中的应用

陈江海

最值问题是一类特殊的数学问题，它在生产、科学研究和日常生活有着广泛的应用，而且在中学数学中也占有比较重要的位置，函数最值问题遍及中学数学各个内容的方方面面，是历年高考重点考查的知识点之一，在高考中，他经常与三角函数、二次函数、一元二次方程、不等式等知识紧密联系，并在一些基础题，小综合的题或难题的形式出现，在高考中有举足轻重的地位。并且由于解法灵活、综合性强，能力要求高，要求全面，故而本人现拟对求函数最值问题的方法进行探究，以便给自己或同学提供一些初等的求解方法。下面就该问题的常用解法，分类浅析如下，供参考.

一、配方法

配方法是求二次函数最值的基本方法，是对数学式子进行一种定向变形（配成“完全平方” ）的技巧，通过配方找到已知和未知的联系，从而化繁为简。如 的函数的最值问题，可以考虑用配方法.

【注意点】：利用二次函数的性质求最值，要特别注意自变量的取值范围，同时还要注意对称轴与区间的相对位置关系.

二、换元法

换元法是指通过引入一个或几个新的变量，来替换原来的某些变量（或代数式），它可以化高次为低次、化分式为整式、化无理式为有理式、化超越式为代数式，便使问题得以解决的一种数学方法.在学习中，常常使用的换元法有两类，即代数换元和三角换元，我们可以根据具体问题及题目形式去灵活选择换元的方法，以便将复杂的函数最值问题转化为简单函数的最值问题，从而求出原函数的最值.例如解不等式：

【注意点】：在用换元法时，要特别注意其中间变量的取值范围.

三、函数单调性法

先确定函数在给定区间上的单调性，然后依据单调性求函数的最值.这种利用函数单调性求最值的方法就是函数单调性法.这种求解方法在高考中是必考的，且多在解答题中的某一问中出现.

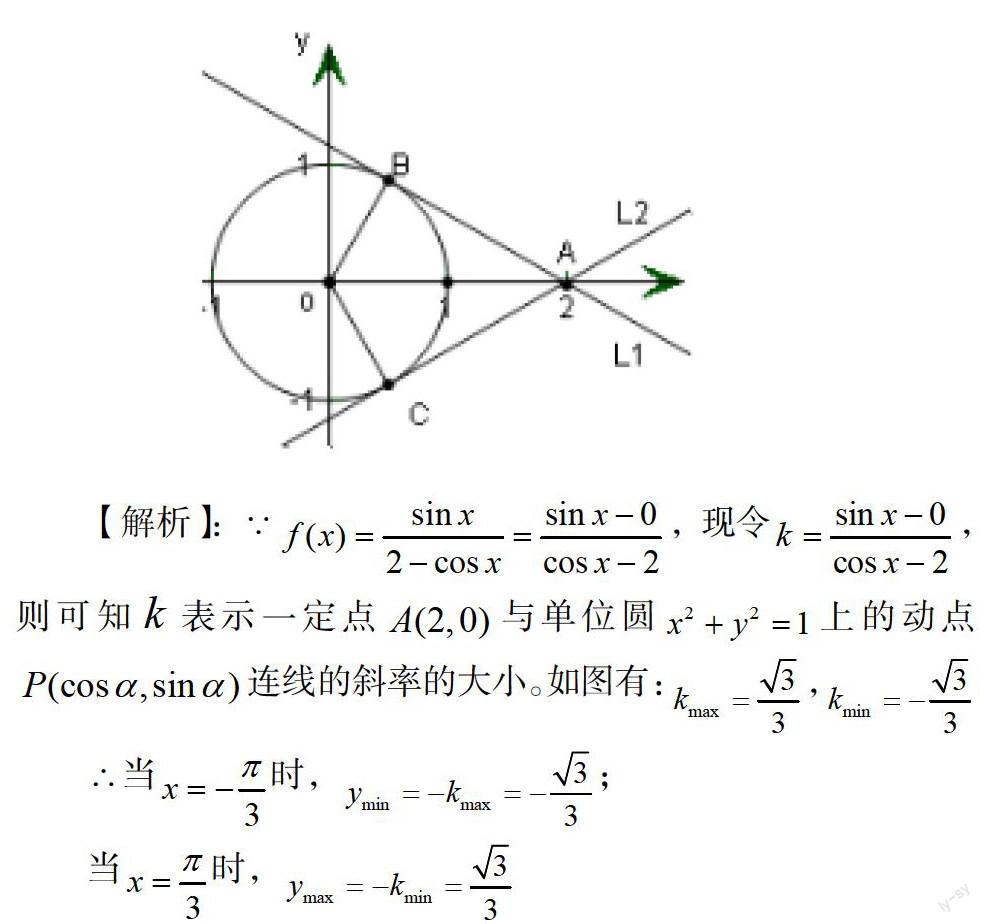
【注意点】：用数形结合的方法求解最值问题，其关键是发现问题条件中所隐含的几何意义，利用这个几何意义，就可以画出图形，从而借助图形直观解决问题。

【总结】：通过以上几种函数最值求法的归纳，可以让自己，也可以对其他同学对一些有关的题目进行解答。尤其是一些综合性强的题目，可以达到事半功倍的作用。函数是中学数学的主要内容，几乎可以用函数为主线，把中学数学各方面内容有机结合起来；许多数学综合题，可以转化为函数的问题进行讨论。