有价证券投资组合的最优化分析

作者简介:牛若琳,女,现为河北大学经济学院国民经济学硕士研究生在读。
摘要:分析有价证券的方法有很多,为了能够方便快捷的分析计算出有价证券的最优组合情况可借助理论分析与软件计算的方法。文章通过运用运筹学中非线性規划的方法并借助简单、容易操作的Excel工具来对有价证券的投资组合进行最优化求解,最后进行预期回报率和风险的分析。
关键词:有价证券;证券投资;最优化分析
有价证券投资者的目标是在承担最小风险的时候获得最大的投资回报。所以该类投资组合优化模型就是在投资组合总回报率的方差(投资风险)不超过某个可以接受的约束值下确定一组投资项目的最优投资比例,以使得总回报率的期望值(预期收益)最大;或者在投资组合总回报率的期望值(预期收益)不低于某个所要求的约束下,使得总回报率的方差(投资风险)最小。下面通过实例来进行求解验证。
如表1是三个可以投资项目1987-2006年的投资回报率,如何在总投资的预期回报率不低于13%的前提下分配这三个投资项目比例才能使得投资组合的风险最小。
表1三个投资项目的单项回报率
年份股票1股票2股票319870.000.070.0619880.040.130.0719890.130.140.0519900.190.430.041991-0.150.670.071992-0.270.640.0819930.370.000.0619940.24-0.220.041995-0.070.180.0519960.070.310.0719970.190.590.1019980.330.990.111999-0.05-0.250.1520000.220.040.1120010.23-0.110.0920020.06-0.150.1020030.32-0.120.0820040.190.160.0620050.050.220.0520060.17-0.020.07
1、模型分析步骤
2、结果分析
2.1 统计计量结果分析
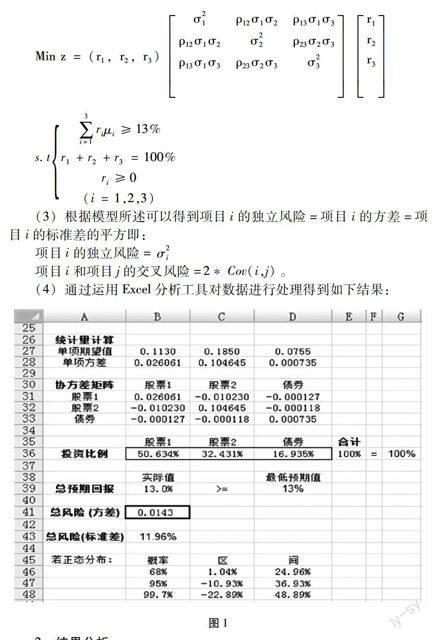
(1)由所得结果可以得到:债券的期望收益最小为0.0755,但其相应的风险也最小为0.000735;而股票2的期望收益最大为0.1850,但相应的风险也最大,股票1的期望收益和风险居中。
(2) 从图中的协方差矩阵可以看出,股票1和股票2、股票1和债券、股票2和债券的协方差均为负数,说明它们是反方向变动的,即一个投资项目的风险增大时另一个的风险会减小。
(3) 根据投资比例结果得当总预期回报率不低于13%时,三个项目的投资比例分别为50.634%、32.431%、16.935%。此时的总风险(方差)为0.0143,标准差为11.96%小于达到最小值。
2.2总预期回报率的置信区间分析
因为有价证券投资有一定的风险,因此还需要对所求结果进行概率分布分析。当投资组合总回报率服从正态分布时,总回报率的置信区间如下:
总回报率的值落在区间[总回报率期望值—总回报率标准差,总回报率期望值+总回报率标准差]即[μ—σ,μ+σ]的概率是68%;总回报率的值落在区间[总回报率期望值—2*总回报率标准差,
总回报率期望值+2*总回报率标准差]即[μ—2σ,μ+2σ]的概率是95%;总回报率的值落在区间[总回报率期望值—3*总回报率标准差,总回报率期望值+3*总回报率标准差]即[μ—3σ,μ+3σ]的概率是99.7%。
根据结果总回报率期望值μ=13%,总回报率的标准差σ=11.96%,所以当总回报率服从正态分布时有以下结果:总回报率以68%的概率落到区间[1.04%,24.96%]中;以95%的概率落到区间[—10.93%,—36.93%]中;以99.7%落在区间[—22.89%,48.89%]中。由此可见区间越大,落到区间的概率接近100%。
2.3预期回报率和风险之间的平衡分析
投资组合优化分析是在风险最小化的前提下寻找收益最大化,但现实中要求我们寻找风险和收益的最佳平衡。为了能够求得这个平衡位置,需要改变收益的最低可接受水平,然后观察对风险的影响。
改变收益的最低接受水平后运用Excel“规划求解”得到表2。表2描述了当预期收益最低可接受水平在某一范围时分别获得最优解的预期收益和风险。
最低预期回报率股票1投资比例股票2投资比例债券投资比例总风险(标准差)预期回报率
8%5.32%2.29%92.39%2.67%8.0%9%14.38%8.32%77.30%3.76%9.0%10%23.45%14.34%62.21%5.59%10.0%11%32.51%20.37%47.12%7.64%11.0%12%41.57%26.40%32.03%9.79%12.0%13%50.63%32.43%16.93%11.96%13.0%14%59.70%38.46%1.84%14.16%14.0%15%48.61%51.39%0.00%16.94%15.0%16%34.72%65.28%0.00%20.76%16.0%17%20.83%79.17%0.00%25.17%17.0%18%6.94%93.06%0.00%29.90%18.0%
通过表2看出首先当预期回报率增加时,风险也随之增加。当收益为14%时,风险为14.16%超过了收益,此后风险越来越大。另外当预期回报率增加时,选择投资项目的投资从最小风险的债券逐渐转向收益最大、风险也最大的股票2;而收益和风险居中的股票1在收益和风险居中时,投资比例最大。
如果没有规定最低预期回报率,则投资者需要根据表2和图2来决定哪一种投资组合在预期收益和风险之间提供了最佳平衡。
3、小结
通过以上的理论分析和实证举例,非线性规划在有价证券的投资组合中得到了很好的使用。在此一定要注意以下几个问题:
(1)单项投资和多项的投资组合中预期的回报是用期望回报率来衡量的,但期望回报率高的不一定是最优选择。
(2)期望收益率只能体现投资的平均回报水平。有价证券投资是有风险的,为了更好的规避由于较大风险带来的损失,需要利用回报率的方差或者标准差来衡量。只有将方差或者标准差和期望收益率结合起来考虑才能更好的选择最优投资组合。
(3)在多项投资组合中,各个投资项目之间是可以互相影响的,这些影响可以使总体的收益风险增大也可以减小。因此应该详细的计算出各个投资项目之间相关系数。
(4)多项投资组合随着预期收益率的变化,其投资比例会发生变化,相应的风险也会发生变化。为了得到预期回报和风险之间的平衡关系则需要根据预期回报率的变化与各投资项目的变化的关系及总风险和预期收益的关系来确定。

