基于博弈论的银行挤兑行为分析
作者简介:田浩(1989 - ),男,宁夏银川人,中央财经大学,金融学院,硕士研究生,研究方向: 金融学。
摘要:本文基于博弈论的简单模型,对商业银行面临挤兑危机进行了分类分析。在假设两位存款人的前提下,分析了挤兑可能发生的情况,银行与两位存款人之间的相互博弈过程,并在不同条件下,得到纳什均衡。
关键词:银行危机;挤兑;博弈论
一、引言
银行的挤兑危机,也称为挤提,是指大量的存款人由于对银行丧失了信心而提前到银行集中提取存款,并最终造成银行的流动性严重不足以及清偿能力出现问题的一种现象。而导致存款人对银行丧失信心的原因主要分为以下几个:一是受到谣言的影响,银行会遭到挤提,例如1960年代代香港银行危机和1980年代的香港银行业危机;二是政治、经济形势变动,会引起存款人恐慌,也会使银行遭到挤提,例如民国时期政治动荡,经济形势异常,经常引起银钱业挤兑风潮;三是银行经营不善,银行经营策略冒进,具有大量不良资产并且银行贷款多投放于高风险行业。纵观历次挤兑历史,被挤兑银行基本都存在着以上三个原因中至少两个。
然而,任何一家银行,不论其如何经营,由于存款保证金率并非100%,一旦遭受挤提,贷款无法及时收回,流动性会变得异常紧张,不仅会使得银行声誉受到很大影响,严重会导致银行寻求收购甚至破产清算。在这样的情况下银行不得不求助于其他银行的拆借资金来满足存款人的提前提款要求,这使得银行面临更大的成本和困难。而单个的银行挤兑很容易演变成存款人对于金融体系的不信任进而引起挤兑风潮的蔓延,对整个社会政治经济的发展带来严重的负面影响。
在2001年加入世界贸易组织之后,中国金融市场将会全方位地对外开放,国内外的金融竞争将会变得越来越激烈,而这也改变了国内金融业结构。国内商业银行不再缺乏竞争对手,这也使得国内商业银行随时会面临银行挤兑危机。现在,实力雄厚经验丰富的老牌外资银行可以随时进入中国金融市场,这会在相当程度上使得我国商业银行原有的储蓄资金外流,造成资本金下降进而导致流动性不足,很容易引起银行危机。
本文通过对银行挤兑危机的分析中,存款人与银行之间的决策行为建立博弈模型,来推断存款人挤兑的行为策略以及银行的应对策略,并讨论存款保险制度对保护银行流动性的作用与其运行机制。
本文讨论了在没有存款保险机制下的银行挤兑博弈模型,进行了纳什均衡的求解,得不同条件下,存款人与银行的策略行为过程与结论。
二、银行挤兑的博弈模型
1、问题描述
在假定没有存款保险制度的情况下,银行与存款人之间的博弈模型可以简单描述为以下情形:
存在三个时期即t=0时期、t=1时期和t=2时期;存在三个博弈参与者:银行、存款人A和存款人B。
在t=0时期,银行吸收资本金α和存款β,存款到期时间为t=2时期。银行在t=0时期将这些资金投入贷款组合γ,即γ=α+β。此时t=0时期结束。在该阶段中,只有银行的行为策略。银行可以选择贷款组合γ为高风险贷款组合θ高与低风险贷款组合θ低,两个不同风险贷款组合到期时间均为t=2时期,且成功概率分别为P高与P低,有P低>P高,到期收益率为R高与R低,有R高>R低。并且有P高R高=P低R低>1,即两个不同风险贷款投资组合的期望收益率相等且均大于1。而两种放贷策略失败的收益均为0。
在t=1时期,存款人A与存款人B的可以选择是否提前取款,银行可以选择是否提前收回贷款。如果存款人在t=1时期选择提前取款,则银行支付其利率为R1;若不选择提前取款,则银行支付其利率为R2(即在t=2时期到期取款),且R2>R1>0。如果银行选择提前收回贷款,则银行可以收回的贷款比率为a,并且有R高>R低>1+R2>1+R1> 1 > a > 0,亦即低风险贷款投资组合成功率要大于高风险贷款投资组合成功率;高风险贷款投资组合成功的收益率要大于低风险贷款投资组合成功的收益率,且大于存款人到期取款的收益率,大于存款人选择提前取款的收益率,并且大于银行在t=1时期回收贷款的收益率a(银行可以选择出售贷款以在t=1时期提前回收贷款)。
在t=1时期,存款人A和存款人B同时可以选择是否提前取款。假定,在t=1时期,银行通过出售贷款来提前回收贷款的款额,只能满足一个存款人的提款要求,而不能同时满足两个提款人的提款要求,即有β(1+R1)2 在t=2时期,银行投资贷款组合可能取得成功,也可能取得失败。 如果银行选择高风险贷款投资组合θ高,若t=2时期时该投资成功,则存款人A与存款人B分别得到收益β(1+R2)2,银行得到收益R高γ - β(1+R2);若该投资组合失败,则存款人A、存款人B与银行得到收益均为0。由此可以得到,如果在t=0时期银行选择高风险投资组合θ高,且t=1时期存款人均不选择提前取款,则t=2时期银行的收益期望为P高(R高γ - β(1+R2)),存款人A和存款人B在t=2时期得到收益的期望为P高β(1+R2)2。 如果银行选择低风险贷款投资组合θ低,若t=2时期该投资组合成功,则存款人A与存款人B分别得到收益均为β(1+R2)2,而銀行得到的收益为R低γ - β(1+R2);若该投资组合失败,则存款人A、存款人B与银行得到收益均为0。由此可以得到,如果在t=0时期银行选择高风险投资组合θ低,且t=1时期存款人均不选择提前取款,则t=2时期银行的收益期望为P低(R低γ - β(1+R2)),存款人A和存款人B在t=2时期得到收益的期望为P低β(1+R2)2。
以上描述为整个简单银行挤兑博弈模型的假设条件及策略执行可能性集。我们假设挤兑可能发生在t=1时期,而银行的应对策略——提前收回贷款,也只有发生在挤兑行为发生的前提下,也只能在t=1时期。而如果存款人A与存款人B在t=1时期都决定提前提款,银行则不得不面临资不抵债的情况,也就是银行必将破产清算。
2、银行挤兑博弈模型的扩展
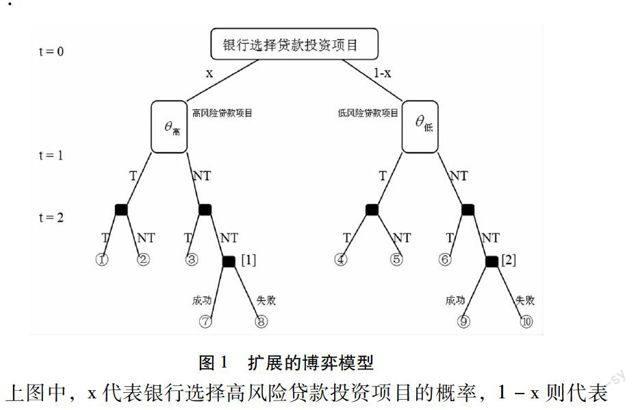
通过上一节的问题描述,我们可以绘制出上述博弈模型的树图如下:
图1扩展的博弈模型
上图中,x代表银行选择高风险贷款投资项目的概率,1-x则代表银行选择低风险贷款投资项目的概率。T代表一位存款人选择提前提款,NT代表不提前取款。①到⑩个节点分别表示存款人A、存款人B和银行的选择可能性集。
第一个节点表示银行选择高风险贷款投资项目,而两位存款人均选择提前提款,则银行得到收益为0,存款人A与存款人B都得到收益aγ2。
第二个节点表示存款人A选择提前提款而存款人B不选择提前提款,在银行选择高风险贷款投资项目的前提下,银行收益为0,存款人A收益为β(1+R1)2,存款人B收益为aγ-β(1+R1)2。
第三个节点表示在银行选择高风险贷款投资项目的前提下,存款人B选择提前提款,而存款人A不选择提前提款,则银行收益为0,存款人A收益为aγ-β(1+R1)2,存款人B收益为β(1+R1)2。
第四个节点表示在银行选择低风险贷款投资项目的前提下,存款人A与存款人B均选择提前提款,则银行收益为0,而存款人A与存款人B的收益均为aγ2。
第五个节点表示在银行选择低风险贷款投资项目的前提下,存款人A选择提前提款,存款人B不選择提前提款,则银行的收益为0,存款人A的收益为β(1+R1)2,存款人B得到的收益为aγ-β(1+R1)2。
第六个节点表示在银行选择低风险贷款投资项目的前提下,存款人B选择提前提款而存款人A不选择提前提款,则银行的收益为0,存款人A的收益为aγ-β(1+R1)2,存款人B的收益为β(1+R1)2。
第七个节点到第十个节点均为存款人A与存款人B在t=1时期不选择提前提款,而使得存款人、银行间博弈进入t=2时期。
第七个节点表示在银行选择高风险贷款投资项目的前提下,存款人A与存款人B均不选择提前提款,如果该高风险贷款投资项目成功,则存款人A与存款人B的收益均为β(1+R2)2,银行的收益为R高γ - β(1+R2)。
第八个节点表示在银行选择高风险贷款投资项目的前提下,存款人A与存款人B均不选择提前提款,如果该高风险贷款投资项目失败,则银行、存款人A与存款人B的收益均为0。
第九个节点表示在银行选择低高风险贷款投资项目的前提下,存款人A与存款人B均不选择提前提款,如果该低风险贷款投资项目成功,则存款人A与存款人B的收益均为β(1+R2)2,银行的收益为R低γ - β(1+R2)。
第十个表示在银行选择低风险贷款投资项目的前提下,存款人A与存款人B均不选择提前提款,如果该低风险贷款投资项目失败,则银行、存款人A与存款人B的收益均为0。
这里依旧强调,若银行选择高风险贷款投资项目,则成功的概率为P高,失败的概率为1-P高;若银行选择低风险贷款投资项目,则成功的概率为P低,失败的概率为1-P低。
3、纳什均衡解
我们已经详细描述了银行与存款人之间的博弈模型。在陈述了我们所需要的假设条件之后,分析了所有可能出现的博弈策略行为。现在,我们需要对以上所述的银行与存款人之间的博弈模型求纳什均衡解。
这里使用逆向归纳的方法来求如上所述的博弈模型的纳什均衡解。
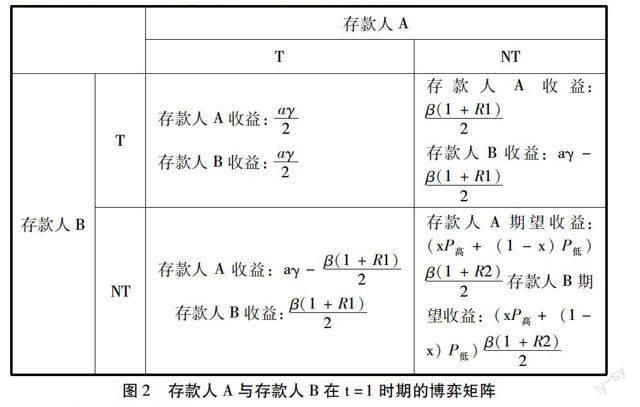
在t=2时期,存在两个决策节点,即(1)银行选择高风险贷款投资组合且存款人A与存款人B均不选择提前提款的情况;和(2)银行选择低风险贷款投资组合且存款人A与存款人B均不选择提前提款的情况。
当P高β(1+R2)2 < β(1+R1)2时,存款人A与存款人B均会选择(T,T)策略,即所有存款人均会选择提前提款。在这种情况下,不论存款人是否知道银行选择的是高风险贷款投资项目还是低风险贷款投资项目,存款人都会选择提前提款(T),所以,在这种情况下,纳什均衡策略为(T,T)。对于银行来说,选择高风险贷款投资项目还是低风险贷款投资项目是没有差别的,因为银行的收益总是0。所以总的均衡为(θ高,(T,T))或者(θ低,(T,T))。
当P低β(1+R2)2 > β(1+R1)2时,存款人A与存款人B均会选择(NT,NT),即两个存款人均不会选择提前提款。因为不论银行在t=0时期是选择高风险贷款投资项目还是选择低风险贷款投资项目,存款人A与存款人B的选择都是(NT,NT)。而给定存款人的选择集(NT,NT),银行会在t=0时期选择高风险贷款投资项目,所以在这种情况下,总的纳什均衡为(θ高,(NT,NT))。
当P低β(1+R2)2 < β(1+R1)2 < P高β(1+R2)2时,存款人A、存款人B与银行之间的博弈需要区分为两个情况,即存款人知道银行会选择高风险贷款投资项目还是选择低风险贷款投资行业,我们称之为信息公开;和存款人不知道银行会做何选择的情形,我们称之为信息不公开。
存款人A与存款人B在知道银行选择高风险贷款投资项目的前提下,会选择策略行为(NT,NT);而在知道银行选择低风险贷款投资项目的前提下,存款人会选择策略行为(T,T),即提前取款,而此时,银行的收益将会为0。综上所述,当P低β(1+R2)2 < β(1+R1)2 < P高β(1+R2)2时,在信息公开的前提下,银行会选择高风险贷款投资项目。即策略组合(θ高,(NT,NT))。
而如果存款人不知道银行会选择何种风险贷款投资项目,即信息不透明的情况下,则要根据银行选择高风险贷款投资项目的概率x来讨论银行与存款人之间策略博弈。
如此,我们令存款人提前提款时的收益与不提前提款时的期望收益相等,就有下列等式:
(xP高+(1-x)P低)β(1+R2)2 = β(1+R1)2(1)
解上列等式(1)中的x,得到一个解x解=1-R11-R2-P低(P高-P低)。当x=x解时,存款人A与存款人B选择提前提款与不选择提前提款时的收益是一样的,即两个选择是我们可以认为是无差异的。
那么,当x > x解时,存款人A与存款人B不会选择提前提款,因为此时不提前提款的期望收益要大于提前提款的收益,则存款人行為策略为(NT,NT)。而给定存款人行为策略(NT,NT),银行会选择低风险贷款投资项目,因为此时对于银行来说,低风险贷款投资项目所获得的收益要大于高风险贷款投资项目。而当银行选择低风险贷款投资项目时,存款人的行为策略会变成(T,T),于是,得到银行与存款人的策略行为纳什均衡解为(θ低,(T,T))。
当x < x解时,存款人A与存款人B将选择提前提款,原因同上。而若给定存款人策略行为(T,T),银行选择高风险贷款投资项目或是低风险贷款投资项目的收益都是一样的,因为银行的收益都是0。所以得到纳什均衡解为(θ高,(T,T))或者(θ低,(T,T))。
三、结论
通过上述讨论发生银行挤兑的博弈模型,我们可以得到以下结论:
当银行选择低风险贷款投资项目时,如果存款人不选择提前提款的收益小于提前提款的收益,存款人会选择提前提款。而如果给定存款人提前提款,银行选择高风险投资还是低风险投资是无差别的。所以银行挤兑是无法通过银行自主选择避免。
当银行选择高风险贷款投资项目时,如果存款人不选择提前提款的收益大于提前提款的收益,则存款人不会选择提前提款。在这种情况下,银行当然会选择高风险贷款投资项目来增加收益,且不会发生银行挤兑。
而如果存款人提前提款的收益小于银行选择高风险投资且客户不提前提款的收益,大于银行选择低风险投资且客户不提前提款的收益,则存款人对于提前提款的选择基于客户对于银行的投资选择的了解程度,即信息是否透明。银行挤兑是否发生也就依据信息是否透明而决定。在这种情况下,银行可以通过是否选择信息透明以及判断存款人的行为策略下来进行博弈,进而避免挤兑的发生。
综上所述,银行挤兑是在存款人A与存款人B均选择提前提款的情况下发生,而经过讨论,不会出现只有一个存款人提前提款的现象,因为只要一位存款人提前提款,另一位存款人也会提前提款来保证自己的收益最大化。
银行挤兑是由于各方面原因而共同造成的危机。在上述第一种情况下,银行是无法通过自主选择来避免挤兑危机的发生。目前国际上通用的做法是引入存款保险制度。但是存款保险制度也是一把双刃剑,不仅存在成本过高等问题,也存在道德风险等问题。
本文只是分析了在其他信息完全透明的情况下,银行投资决策与存款人之间的博弈过程,并得到一些条件下的纳什均衡解,为银行通过自身决策防止挤兑危机的发生提供了一些理论依据。(作者单位:中央财经大学)
参考文献:
[1]乔海曙,李远航. 银行挤兑危机的博弈分析[J],财经理论与实践(双月刊),2006,第三期
[2]Chari, V.V and R. Jaganattan, Bank Panics, Information, and Rational Expectations, Journal of Finance, 1988, XLII
[3]Jacklin, C.J., Market Rate versus Fixed Rate Demand Deposits, Journal of Monetary Economics, 1993, 32
[4]Fernando Vega-Redondo, Economics and the Theory of Games, 2006
[5]韩冰,凤凰涅磐——问题银行救助机制研究[M],北京:中国金融出版社,2007
[6]李义奇. 银行挤兑时各利益主体行为的博弈分析[J],经济经纬,2000,6
[7]HD. Morris.Probability and statistics. Second Edition. New York: Addison - Wesley publishing Company, Inc, 1975
[8]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,1996
[9]朱中云,银行挤兑与存款保险的博弈分析[J],中国学术期刊电子杂志,1994
——博弈论

