含有磁滞逆的状态反馈非线性系统动态面控制
吴金龙
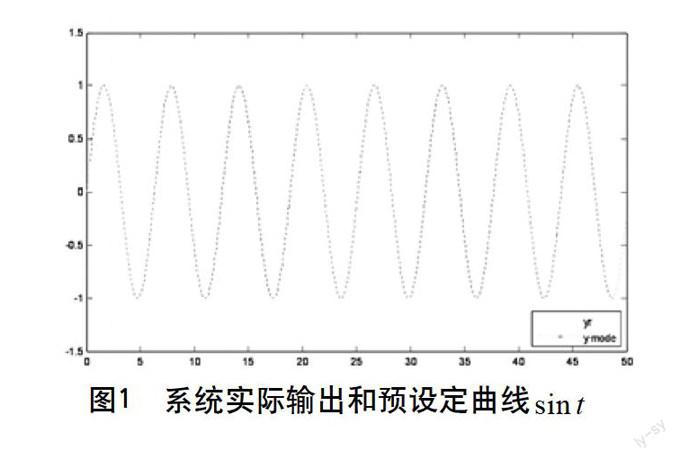
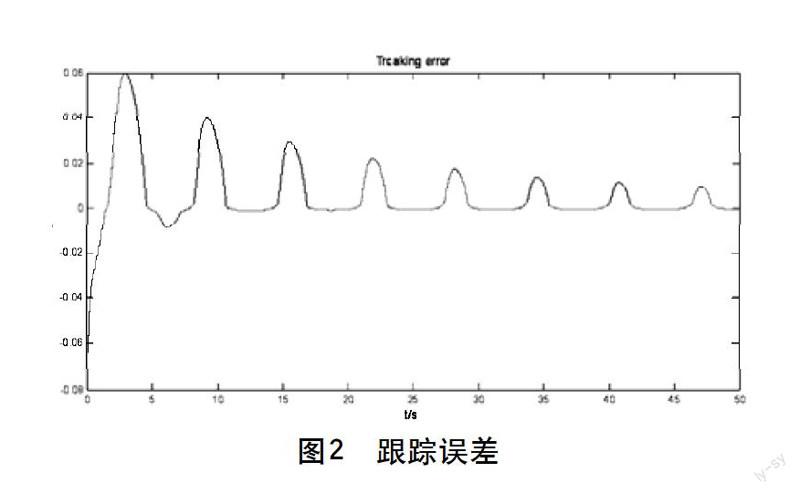
摘要:针对一类带有Revised Prandtl-Ishlinskii(RPI)磁滞的严格状态反馈非线性模型,通过引入磁滞逆模型抵消输入中的磁滞输入项,提出了一种改进的鲁棒自适应动态面控制方案。本方案解决了采用反推法时出现的“微分膨胀”问题,保证闭环非线性系统所有信号半局一致有界。仿真结果证明了控制律的有效性。
关键词:磁滞逆;动态面控制; 性能
中图分类号:TP13 文献标識码:A 文章编号:1672-3791(2015)10(a)-0000-00
0引言
磁滞是一种常见的非线性现象,很多智能材料制作的装置中都会出现,比如压电陶瓷驱动器[1]。磁滞现象的存在制约了闭环控制系统的精确度和稳定性,容易产生震荡[2]。由于现代工业大规模采用以智能材料为核心部件制作的装备,因此系统中的非线性磁滞现象受到国内外学术界的广泛关注[3]。
反推法在非线性系统中常被用来设计控制器。但是反推法在设计高阶系统控制器时会出现“微分膨胀”问题,并且给计算机带来极大的计算量。
在处理磁滞问题时,有鲁棒自适应[4]和建立磁滞逆模型[5, 6]两种方法,由于建立磁滞逆模型对于模型的精确性要求较高并且推导复杂,所以大部分学者采用鲁棒自适应方法来克服系统中的磁滞现象,本文采用构造磁滞逆的方法来解决非线性系统的控制问题。通过设计合适的Lyapunov函数,保证闭环系统所有信号一致有界。仿真结果表明所设计的控制器具有较好的跟踪性能。
参考文献:
[1]谷国迎, "压电陶瓷驱动微位移平台的磁滞补偿控制理论和方法研究," 博士, 上海交通大学, 2012.
[2]Z. Xiuyu, W. Jing, and L. Cuiping, "Robust adaptive dynamic surface control for metal cutting system with hysteresis input," in Intelligent Control and Automation (WCICA), 2014 11th World Congress on, 2014, pp. 1534-1539.
[3]曹淑瑛, "超磁致伸缩致动器的磁滞非线性动态模型与控制技术," 博士, 河北工业大学, 2004.
[4]贾涛, 刘军, and 钱富才, "一类非线性时滞系统的自适应模糊动态面控制," 自动化学报, pp. 83-91, 2011.
[5]L. Sining, S. Chun-Yi, and L. Zhi, "Robust Adaptive Inverse Control of a Class of Nonlinear Systems With Prandtl-Ishlinskii Hysteresis Model," Automatic Control, IEEE Transactions on, vol. 59, pp. 2170-2175, 2014.
[6]L. Sining, S. Xinjun, L. Zhi, and S. Chun-Yi, "Inverse control of a class of nonlinear systems with modified generalized Prandtl-Ishlinskii hysteresis," in IECON 2012 - 38th Annual Conference on IEEE Industrial Electronics Society, 2012, pp. 2319-2324.

