在线产权交易的电子竞价应用研究

张平春　高国伟

摘要：目前我国对在线产权交易的电子竞价方式研究较少，且均是研究买方的竞价策略及博弈论的分析。因此文章基于产权转让方的角度，以转让方获得最大利益为标准进行对电子竞价的一口价、第一价格竞价、次高价竞价、连续多次竞价等几种竞价模式进行假设与建模的分析与比较，通过这四种常见竞价方式的比较最后得到，在线产权交易的电子竞价模式下，考虑到时间与效率的关系，应该选择次高价竞价方式作为在线产权交易电子竞价的首选方式。

关键词：在线产权交易；一口价；第一价格竞价；次高价竞价；连续多次竞价

随着“互联网+”模式的推进，在线产权交易模式已经完全替代传统（手工）产权交易模式，实现由传统线下模式向现代在线模式的转变。在在线产权交易模式中，根据《产权转让办法》的规定，在对产权交易征集到两个及两个以上意向受让方时应通过竞价的方式进行。在在线产权交易模式下，竞价实现了由传统的拍卖到电子竞价模式的转变。

电子竞价一直都是被研究的重点，尤其是在“互联网+”的时代显得格外重要。所谓的电子竞价是区别于电子拍卖的一种通常使用网络并通过网络以竞价或议价为主，遵循“价格、时间、数量优先”的原则将物品（服务）出售或出让给竞价高（低）的竞价者的独立的在线交易方式。

本文分为五部分，第一部分是对电子竞价方式的一口价竞价模式的概述分析；第二部分是对电子竞价方式的第一价位竞价模式的概述分析；第三部分是对电子竞价方式的次高价竞价模式的概述分析；第四部分是对电子竞价方式的连续多次增价竞价模式的概述分析；第五部分是对以上四种电子竞价的方式的比较，并最终得出结论。

一、一口价竞价模式

在一口价竞价模式中，一口价包括固定一口价、临时一口价和持久一口价。其中临时一口价和持久一口价中包含着固定一口价和其他的竞价方式，因此这三种一口价竞价方式可以分为固定卖价方式和其他竞价方式。在现实生活中eBay网站的大部分均是通过一口价进行的，并且一些学者也给出了一口价存在的必要性。

假设：1. 单项物品竞价并且其成本为c，并且竞价人为风险中性，在竞价周期[0，t]内有n人参与竞价，并且服从λ为参数的泊松分布，转让方设置的一口价为：

B∈[v1，v2]

2. vi[v1，v2]是竞价者i的估价，且分布函数和密度函数为F（vi）和f（vi），设定一个门限值v0。

根据以上可得竞价人的竞价期望和购买期望分别为：

E（bid）=[F（x）]n-1f（x）dx

E（buy）=vi-B

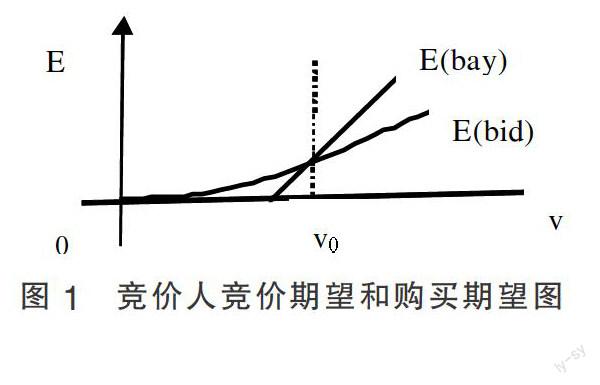
为解决模型令竞价期望与购买期望相等，即[F（x）]n-1f（x）dx=vi-B得到图1。

从图1可以看出在v0点时是竞价和购买的临界点即他们的门限值，在v0之前竞价人会选择竞价方式，在v0之后会选择固定购买方式。根据一口价卖家收益分析，卖家在固定一口价、临时一口价和持久一口价中所对应的收益为R1、R2和R3，并且有R1=B-c；R2=vf（v）dv-c或R2=B-c；R3=-c或R3=vf（v）dv-c或R3=B-c。

作为一口价的竞价模式，但从竞价原则上可知，当转让方把标的物的价格设置太高，则不会有受让方选择一口价方式交易；如果转让方的价格设置太低，则又会导致不会将标的物转让给心理真实估价最高的受让方，影响自己的收益。因此根据以上分析可知，在三种模式同时选择固定卖价方式时它们的收益是相同的，即R1=R2=R3。在v0点之后转让方通过竞价则会收益更大，其竞价方式在这不再赘述。

二、第一价位竞价模式

（一）第一价位竞价模型

第一价位竞价是第一价格密封拍卖的延伸，是指每个参与竞价的竞价人在不知道其他竞价人报价的同时提交一个自己的对标的物的报价，出价最高者获得该标的物并且其支付的价格就是其所报出的价格。

任何一个竞价模型都涉及到两个主体（转让方和受让方）的利益，并且这两个主体的利益是发生冲突的，这里从受让方的角度进行论证第一价位竞价模型。

假设：假设共有n个风险中性的转让方参与竞价，每个投标人i对标的物品的真实心里估价为vi，其参与的报价为Bi服从[0，1]上均匀分布，效用函数为Ui，意向受让方的竞价者的收益为y，其效用函数通过Ui（y）=y所确定。

根据在线产权交易的博弈模型可知，参与产权交易的主体是产权交易所和意向受让方（不同的意向受让方的竞价风险均为中性）。根据密封一级价格拍卖的基本理论可知受让方的效用函数为：

U（vi-Bi）=u（vi-Bi）Bin-1

通过对上式的求导并且将Ui（y）=y代入，最后求解得：

受让方的报价为：Bi=vi

（二）第一价位竞价模型缺点分析

从受让方方面来看，在第一价位竞价机制下，参与竞价的受让方之间的报价竞争属于不完全信息下的静态博弈，为了使受让方的报价达到最优，每个标的物的竞价中的受让方的数量应该控制在6～9人，最多不能超过15人，并且在不限制参与竞价者人数的情况下，这种竞价机制不能保证参与竞价的受让方的报价是最优价格。

从转让方方面来看：根据以上模型可以知道，当n无限增大到无穷时，受让方的报价趋向于自己心里的真实估价，此时转让方的收益最高，可以得到受让方的全部价值，并且这种机制下的理想的模式与现实的距离差距很大；现实中转让方在产权转让的竞价方式在挂牌公告之前就已经确定，并且意向受让方的征集是由产权交易所通过在线产权交易平台进行征集，征集到的意向受让方的数量不受转让方的控制，并难以保证每次进行电子竞价的意向受让方的数量控制在6～9人。

三、次高价竞价模式

（一）次高价竞价模式概述

所谓的次高价竞价是根据第二价格密封拍卖延伸过来的竞价机制，目前在我国第二价格密封拍卖方式具体的应用和时间相对较少，从理论上来看，它确实是一种在体现公平的同时也考虑效率的有效的竞价机制。它与第二价格密封拍卖的相同点在于都是以最高价获得竞价成功的标准，以第二高价格作为最后的支付价格；不同点在于，次高价不存在密封情况。在线产权交易中的次高价竞价是指意向受让方们同时提交竞价的价格，由产权交易所同时对所提交的竞价结果进行验看，并最后确定真正的受让方的活动。

单从最后的竞价结果来看，次高价竞价模式相对于最高价竞价模式最后的竞价结果会让转让方没能够得到最优的价格。但是综合考虑，最高价竞价的结果不一定是意向受让方真正的心理价格，通过次高价竞价方式能够获得转让方心理的真实价格，并且可以把最高价和次高价之间产生的差价作为对意向受让方报出自己真实心理价格的一种奖励。

（二）次高价竞价模型推论

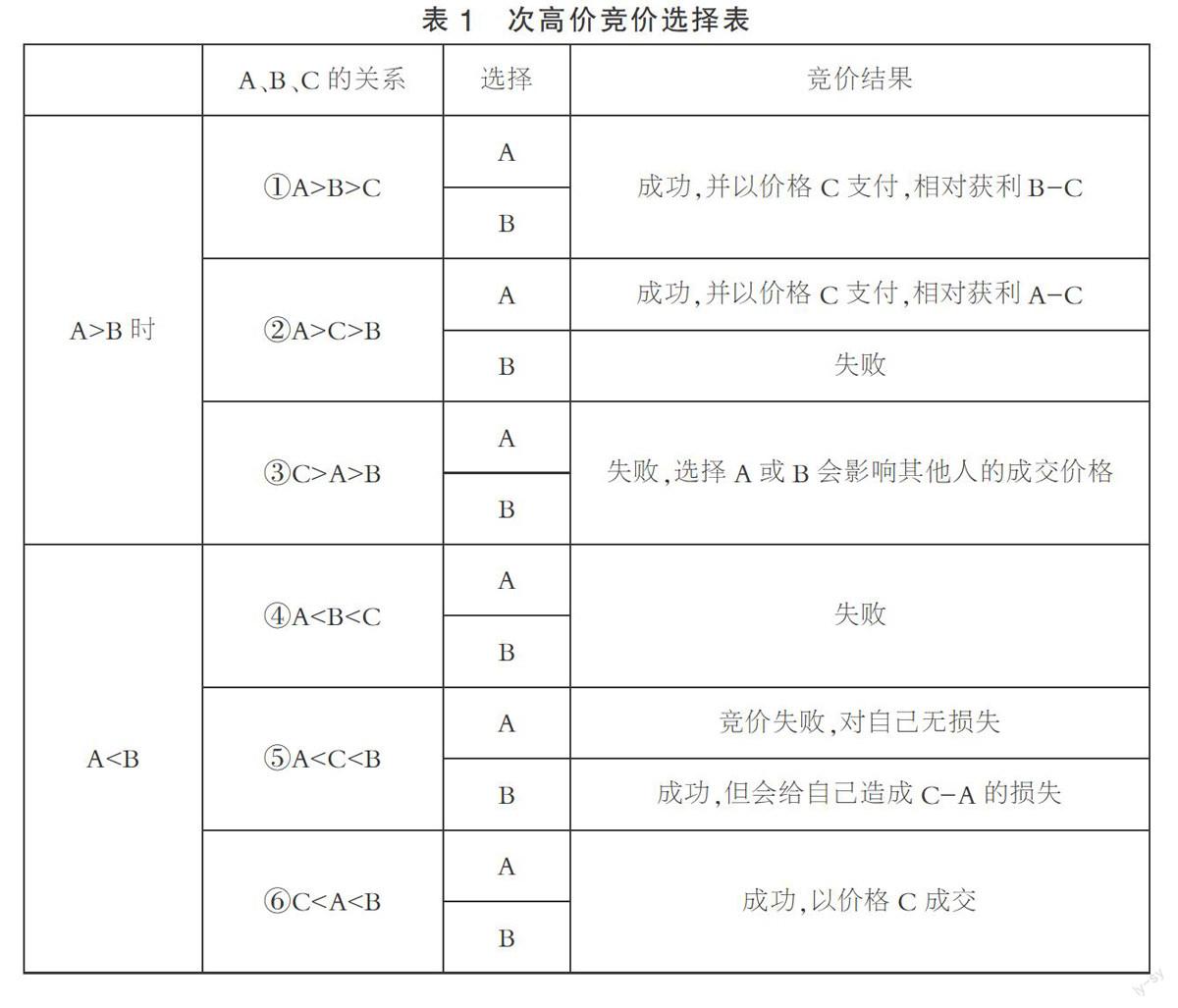
假设：参与竞价的意向受让方均是风险中性的且私人价值模型均独立，竞价过程中不存在破坏竞价现象，并且仅考虑标的物的价格因素。可以令甲竞价者对某标的物的真实心理价格为A，所提交的报价为B，其他所有竞价者中的最高价为C，如表1所示。

根据表1分析可知，当真实心理价格高于报价高于其他人最高价时，无论选择真实心理价格还是报价都会竞价成功，并且会以价格C进行支付，相对获利B-C或A-C；当真实心理价格高于其他人最高价高于报价时，此时如果选择真实心理价格作为提交的报价的话会竞价成功，并且以价格C支付，相对获利A-C，否则竞价失败；当其他人最高报价高于真实心理价格高于报价，此时无论选择何种价格作为报价均会竞价失败。

当真实心理价格低于报价低于其他人最高价时，此时无论选择何种价格作为报价均会竞价失败；当真实心理价格低于其他人最高价低于报价时，选择真实心理价格作为报价虽然会导致竞价失败，但不会给自己带来损失，如果选择高于心理真实价格的报价的话虽然会竞价成功，但会给自己造成损失；当其他人最高价低于真实心理价格低于报价时，无论选择何种价格作为报价，均会赢得竞价并且会以价格C进行支付。

经过分析以上的6种情况可知：选择高于真实心理价格的报价则会有竞价失败的风险，选择低于真实心理价格的报价则会有亏损的风险。综上所述，基于次高价竞价方式的前提，本着有利于意向受让方的原则，作为意向受让方的竞价者必定会选择自己真实心理价格进行报价。也就是说在次高价竞价方式下，竞价者会把自己的心理真实的价格作为报价。

四、连续多次增价竞价模式

所谓的连续多次增价竞价方式即英式拍卖的引申，由多人连续、多次、递增的方式进行竞价，最后出价最高的竞价者竞价成功，并且以其所出的价格进行支付的竞价方式。考虑到在竞价过程中的时间、效率等问题，在这种多次增价模型中的涉及到一个关键的部分即竞价梯度的设计问题。

模型假设：参与竞价的意向受让方每次出价梯度不得小于a，在所有n（n≧2）个参与竞价的意向受让方m的估价为Vm，Vi是最高估价，Vj是次高估价。

则一定会有：Vi>Vj

设第K个意向受让方出价为Yk时，其他受让方不再参与竞价，则成交价格为Yk，则有：

Yk≦Vi（受让方的出价必定不会高于自己的心理估价）

根据受让方出价Yk与最高估价Vm和次高估价Vj的关系得到表2。

根据表2可知：

1. 当k≠i时即第k个意向受让方所出报价不是所有意向受让方中的估价最高者时：一定会有Yk+a>Vi，否则一定会有人再次出价，并且会高于Yk；根据这项关系式可以推导出 Yk>Vi-a ；当Yk>Vj 时即第k个意向受让方出价高于所有人中的次高估价时，此式成立的前提是Yk一定是最高估价的出价，并且这与k≠i相悖，所以Yk>Vj不存在，因此只有Yk≦Vj 即第k个意向受让方出价一定是不大于所有人的次高估价的。

2. K=i时即第k个意向受让方所出报价是所有意向受让方中的估价最高者时：①当YkVi即受让方的出价Yk再加一个竞价梯度a就会高于次高估价Vi，由于Yk是最后的成交价格即报价最高，否则次高估价者一定会再次出价。②当Yk≧Vj即第k个意向受让方所出报价不小于次高估价时， Yk≦Vj+a即第k个意向受让方所出报价不大于次高估价于竞价梯度之和。基于第k个意向受让方所出报价不小于次高估价的前提，并且K就是最高估价人，因此如果想在产权转让的电子竞价中获胜就必须所报价要不小于次高估价者的估价。在Vi>Vj的情况下，如果最高估价者想获得竞价成功，最多出价Vj+a即可赢得竞价。基于以上的分析：Yk≦Vj+a。最高估价的竞价者在竞价时一定会在不大于自己估价的前提下，在目前最高报价的基础上再加一个竞价梯度的价格即可获胜，否则与现实买方帕累托最优不符。

根据以上分析：

Vj-a

当竞价梯度a→0时，Yk=Vj。即在连续多次增价竞价方式下，随着竞价梯度的逐渐缩小，最终的产权交易的电子竞价成交价格逐渐收敛于次高估价。

五、结论

通过对一口价、第一价格竞价模式、次高价竞价模式和连续多次增价竞价模式等在线产权交易的竞价方式的分析比较可知道，在这四种竞价方式下基于转让方的最优期望收益，最终收敛于次高估价。基于时间、效率等方面的考虑，当在线产权交易进行竞价方式时为了使转让方获得最大的收益，应该选择次高价的电子竞价方式。

参考文献：

[1]Friedman L A competitive biding strategy[J]operations Research， 1956（01）.

[2]Milgrom P R ，weber R J .A theory of auctions and competitive bidding[J].Econometrica，1982（05）.

[3]刘树林，汪寿阳，黎建强.投标与拍卖的几个数学模型[J].管理科学学报，1998（02）.

[4]Leszczyc P .Qiu C . Hey Empirical testing of the reference-price effect of buy-now price in intemet auctions [J].Journal of retailing，2009（02）.

[5]吉吟东.网上英式拍卖中的卖方策略研究[D].电子科技大学，2006.

[6]Budish E B.Takeyama L N. Buy prices in online auctions Irrationality on the intemet [J].Economic Letters，2001（03）.

[7]倪冠群，徐寅峰，郑斐峰.网上一口价在线拍卖的定价策略设计[J].管理科学学报，2011（03）.

[8]杨兴丽，陈霞，吕廷杰.一口价网上拍卖方式中卖方收益分析[J].北京邮电大学学报（社会科学版），2007（04）.

[9]Brand F . Full private Auctions in a Constant Number of Rounds [C]//Proc. Of the 7th .Annual conference on Financial Cryptography.Munich，Germany：[s.n]，2003.

[10]陈德湖.基于一级密封拍卖的排污权交易博弈模型[J].工业工程，2006（03）.

[11]张帆，孙卫.报价-购买博弈分析[J].预测，2002（06）.

[12]张利荣，王素梅.一级密封招标的最优报价策略研究[J].系统工程理论与实践，2005（06）.

[13]刘树林，戎文晋.搜索引擎广告的机制设计理论与实践[M].科学出版，2010.

[14]吕慧娟.略论第二价格密封拍卖[J].当代经济，2007（09）.

[15]Tang F. Equilibria Y O. In second price auctions with participation costs[J].Journal of theory，2006（130）.

[16]Vickrey W . Counter-speeulation .auctions ，and competitive sealed tenders[J]. Journal of Finance，1961（01）.

[17]洪宇.应用第二价格密封拍卖理论的招标模式研究[D].天津大学，2005.

[18]诚然，吴文升，孙卓睿.第二价格密封拍卖理论框架下政府投资项目招投标模式改进研究[J].工业技术经济，2011（03）.

[19]邹英.企业国有产权交易方式选择研究[D].贵州大学，2007.

[20]李文童.企业国有产权交易中的拍卖机制研究[D].苏州大学，2009.

*基金项目：国家自然科学基金项目“客观知识体系中的语义传递模型研究”（71073017）。

（作者单位：辽宁师范大学）