整体思想的应用

陈德前

数学思想是数学基础知识的重要组成部分，是解决数学问题的灵魂和精髓.

在数学学习中，一定要重视对常用数学思想的挖掘、提炼、应用.下面举例说明整体思想在解决方程组问题中的应用，供同学们学习时参考.

点砰：本题考查二元一次方程组的解的定义和解二元一次方程组，解题的关键是理解二元一次方程组解的定义和解二元一次方程组的方法.具体求解时，用代人法或加减法求出a、b的值，即可得到答案.如果巧妙运用整体思想，可使解法更简捷.

点译：将方程组中相同的部分看作一个整体（如本例中的3x+2y）代入消元，往往有意想不到的效果.

三、解应用题

1.直接整体处理，

例3（2014年苏州）某地准备对一段长120m的河道进行清淤疏通.若甲工程队先用4天单独完成其中一部分河道的疏通任务，则余下的任务由乙工程队单独完成需要9天：若甲工程队先单独工作8天，则余下的任务由乙工程队单独完成需要3天，设甲工程队平均每天疏通河道xm，乙工程队平均每天疏通河道ym，则x+y的值为_____.

解析：根据条件“若甲工程队先用4天单独完成其中一部分河道的疏通任务，则余下的任务由乙工程队单独完成需要9天”与“若甲工程队先单独工作8天，则余下的任务由乙工程队单独完成需要3天”中隐含的相等关系，建立关于x、y的方程组，并应用整体思想，即可求得x+y的值，由题意，列方程组，得：

2.变形后整体处理.

例4 （2014年滨州）某公园“六一”期间举行游园活动，成人门票和小孩门票均有较大的折扣.张凯、李利都随他们的家人参加了本次活动，王斌也想去，就打听张凯、李利买门票花了多少钱.张凯说他家去了3个大人和4个小孩，共花了38元钱；李利说他家去了4个大人和2个小孩，共花了44元钱，王斌家计划去3个大人和2个小孩，请你帮王斌算一下，需准备_____元钱买门票.

点译：本题考查了二元一次方程组的应用，解答此类问题的关键是找到相等关系，列出方程组.问题需要求3个大人和2个小孩所需要的门票费用，因此不需要求出方程组的解，从整体上变形求解即可得到答案.

2.（2014年黔东南）某超市计划购进甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元，求每件甲种、乙种玩具的进价分别是多少元.

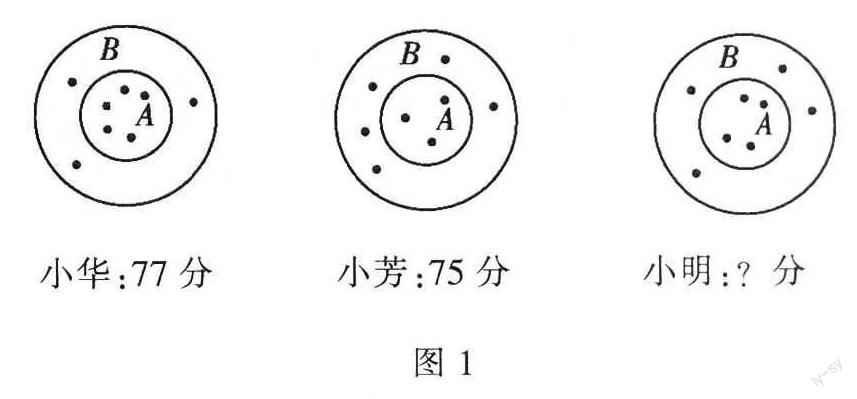
3.在学校组织的游艺晚会上，掷飞镖游艺区游戏规则如下：如图1，掷到A区和B区的得分不同，A区为小圆内部分，B区为大圆内小圆外的部分，现统计小华、小芳和小明掷中情况与得分情况如图1所示.

依此方法计算小明的得分为多少分.

参考答案：

1.A

2.每件甲种玩具的进价是30元，每件乙种玩具的进价是27元.

3.小明的得分为76分.