等腰三角形最怕啥
李林明


小朋友,等腰三角形是三角形中的“另类”,它仰仗着自己的优势“打家劫舍,胡作非为”,这也许让你很头痛。其实,等腰三角形是只“纸糊的老虎”,只要你懂得要领,向它的“软肋”轻轻一戳,它就会应声倒地!
招法1——擒“角”
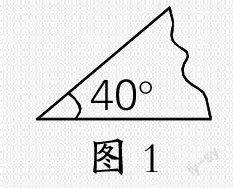
例1.图1是从一个等腰三角形上撕下来的一个角,问原等腰三角形的其他两个角可能是多少度?我是这样解的。
由于等腰三角形具备两个底角相等的性质,所以根据三角形内角和的关系,可借助“顶角+底角×2=180°”来表达。这个公式,就是我们擒“角”的利器!
因为题目给出的“角”并未确定,所以在解答时就要考虑到这样的两种情况:
情况1:当所给的角为等腰三角形的顶角时,每个底角的度数是:(180-40)÷2=70(度)。
情况2:当所给的角为等腰三角形的一个底角时,它的顶角度数为:180-40×2=100(度)。
这样,这个等腰三角形余下的两个角的度数分别为:70度、70度;40度、100度。
招法2——捉“腰”
例2.在图2的方格图中选一个交叉点(用C表示),连接ABC使它成为一个等腰三角形。问:一共可连出多少个等腰三角形?我是这样解的。
在等腰三角形的“边”中,两腰相等。只有在极特殊的情况下,如等边三角形(属于特殊的等腰三角形)底边的长度才与两腰相同。理清了它们之间的这层关系,在应对上面问题时也就增添了必胜的信心。
情况1:当AB为等腰三角形的“底”时,可以得到△C1AB、△C2AB(如图3、图4)两个等腰三角形。情况2:当AB为等腰三角形的一个“腰”时,我们采用发散思维,向每个方向顺次连接,就可得到△C3AB、△C4AB、△C5AB、△C6AB(如图5-8)四个等腰三角形。综合两种情况,一共可以连出6个等腰三角形。“卡通数学”参考答案
车的速度是35千米/时,步行的速度是4千米/时。

