博弈论在大学生活中的应用
谢平


[摘 要]博弈渗透到人们生活当中的点点滴滴,无数场博弈便构成了人生。每个理性的经济人都力图在博弈中获得最大支付,实现自身利益最大化。纵观国内外,博弈的思想在古代就已被人们熟练运用。《孙子兵法》,“囚徒困境”等无不印证了博弈论的精髓。直至今天,从石油之战,到股票买卖,再到日常人际关系等现象均可用博弈论分析。总之,博弈论涉及经济、政治、文化等方方面面,具有极强的实用性。文章拟探讨大学生活中的博弈论,贴近实际又不失趣味。
[关键词]博弈论;大学生活;经济人
[DOI]10.13939/j.cnki.zgsc.2015.45.214
1 静态博弈:混合策略纳什均衡
在纯策略博弈中,通过画下划线的方法可以找到纳什均衡。然而并不是所有纯策略博弈都有纳什均衡。但倘若给参与人的每个策略附加一定概率,构成混合博弈,此时运用混合策略曲线法,结合数学推导,就必然能找到纳什均衡。假设A,B同学分别以“a1,a2”,“b1,b2”的概率选择自习和看电影,其支付矩阵为:
在此图形中,A,B同学混合策略曲线的两端点分别为(0,1),(1,0)和(0,0),(1,1)。两曲线唯一的交点(1/2,3/4)表示A,B同学以(1/2,1/2)和(3/4,1/4)的概率选择自习,看电影时,博弈达到均衡。此时双方均没有单独改变策略的动机,期望支付也最大。
2 静态博弈下的古诺模型
一个大学食堂的优劣直接关系到同学们的生活质量水平。现假设某大学有两个食堂,第一食堂自主经营,第二食堂对外承包,现研究其在静态博弈下的策略选择问题。
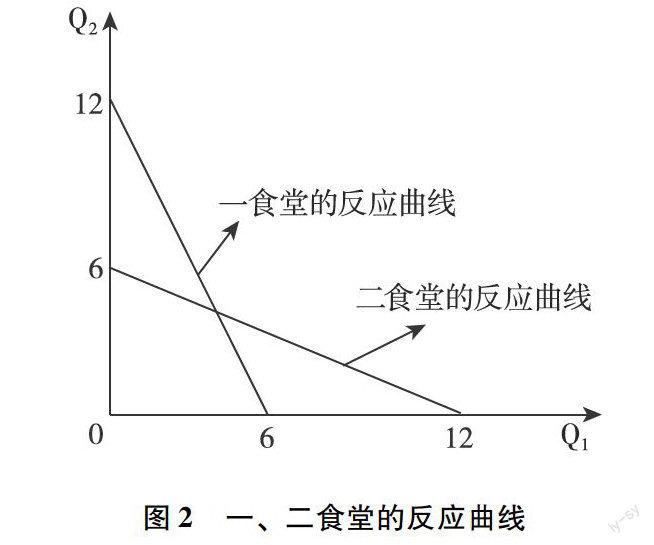
静态博弈要求双方参与人同时采取行动,有古诺模型和伯特兰德模型,这里讨论前者。古诺模型下假定市场只有两个厂商,生产相同产品等等。一,二两个食堂可视为两个寡头厂商,他们提供相同的饭菜。为简单起见,假设成本为0,面临的反需求函数为P=24-2Q:
因此,当两个食堂均以8元的平均价格供应饭菜时,双方销量均为4000份,此时达到了静态博弈下的纳什均衡。联系实际生活,上外食堂一顿饭菜的平均价格还不足8元,比较符合学生的利益。
其实,上述案例若在动态博弈下,也可根据斯塔克伯格模型找到均衡点。如果一食堂先采取行动,二食堂在一食堂已经制定的产量上选择策略。其他条件不变时,最终会在Q1=6,Q2=3,P=6 处达到纳什均衡。与古诺模型相比,两种都是产量竞争下的垄断模型,不考虑市场价格的影响。但在斯塔克伯格模型中,先行动的参与人不再有反应函数。并且在一食堂先行动的情况下,其产量是二食堂产量的2倍,相比两者同时行动下的产量(Q1=Q2=4),一食堂提高了2000份,而二食堂则降低了1000份。这实际上也与经济学中的“先动优势”遥相呼应。
笔者以案例作为骨架,支撑起全文脉络,易于理解。相关案例更是从大学生活中找寻灵感,贴近实际,适用性强,便于引起读者共鸣。文章遵循由浅入深的原则,循序渐近,步步为营。通过将经济学知识,数学知识,博弈论和大学生活四者有机结合,挖掘出简单生活背后的奥秘,希望能进一步提高读者对博弈论的认知和感悟,巧妙运用到以后的学习生活中。总之,学好博弈论,就不会在面临众多选择之时感到手足无措,就会始终站在理性经济人的角度认真思考,做最正确的选择,实现利益的最大化。
参考文献:
[1]胡希宁,贾小立.博弈论的理论精华及其现实意义[J].中共中央党校学报,2002(2).
[2]黄韬,易宪容,高占军,等.博弈论的发展与创新——1994年诺贝尔经济学奖获得者成就介绍[J].财经问题研究,1995(5).

