企业激励下的员工行为选择

王海 唐崇

[摘 要]在现代企业的管理中，员工作为企业发展中的重要因素，在一个假设完全信息的情况下，企业如何与长期合同制与短期雇佣者的员工进行不同的博弈，从而实现双方的最优选择，即企业合适的激励措施引导员工做出正确的行为选择，对整个企业的发展至关重要。

[关键词]企业激励；完全信息；动态博弈

10 13939/j cnki zgsc 2015 51 209

1 引 言

升职激励（Promotion Incentive）是一种广泛应用的人力资源管理模式，已被众多案例证明能够有效晋升企业人力资。升职激励就是企业领导将员工从低一级的职位晋升到新的更高的职务，同时赋予与新职务一致的责、权、利的过程，往往也伴随着工资薪酬的提高。作为企业一种重要的激励措施，企业职务晋升有两大功能，一是选拔优秀人才，二是激励现有员工的工作积极性。企业从内部提拔优秀的员工到更高、更重要的岗位上，有利于激励人才价值的发挥和潜在价值的晋升，能更好地从企业内部培养各岗位的接班人，对人力资源价值的形成与发挥有重要的引导作用，从而对员工和对企业发展都有重要意义。

但由于受制于机会缺失、能力不济、动机匮乏等原因，员工在工作中可能得不到合适的晋升机会，由此在工作产生悲观的态度，难以有效激励员工充分发挥聪明才智，从质量上对公司的人力资本的晋升产生负面影响，甚至进而可能导致的员工离职则从数量上对公司的人力资本的晋升产生负面影响。

作为平等的市场与法律主体，双方均有互相选择的权利，短期内员工是否努力、企业对员工是否晋升，长期内员工是否离职，都是双方基于完全信息博弈的结果。本文试图通过短期与长期时间内企业与员工的晋升博弈，探究是否存在对双方均有利的均衡结果，以达到改善资源配置、实现企业与员工共同发展、晋升社会福利、加速形成我国人力资本的作用。

2 短期雇佣员工的博弈行为选择

完全信息动态博弈是指博弈参与人的行动有先后顺序，且后行动者在自己行动之前能够观测到先行动者的行为，并相机而动。在应用中，习惯于用扩展式表述来描述和分析，相比于静态博弈的战略式表述，它扩展了参与人的战略空间，给出了每个战略的动态表述：谁在什么时候行动，每次行动时有些什么具体行动可供选择，以及知道些什么。

2 1 纯战略纳什均衡

短期内员工能否得到晋升是员工与企业的博弈过程，即员工在工作中表现得是否努力以寻求晋升，而企业在考察员工之后做出是否晋升的决定。

并做如下假设：假设员工和企业是参与人，双方都是“理性经济人”，即决策的目标都是利益最大化。员工个人追求效用最大化，企业追求润最大化。员工的效用最大化的考虑有：努力工作可带来更大的晋升机会，但会损失闲暇时间，两项构成效用。企业利润最大化的考虑有：晋升员工带来的人力资本提高进而企业营收提高，但会增加薪酬支出成本和其余未晋升员工的内部关系协调成本，两项构成利润。员工的策略是努力或不努力，企业的策略是对晋升员工或不晋升员工。同时假定，员工不努力会降低企业的利润；员工不努力却能获得晋升也是可能出现的，可能是企业基于激励员工等的考虑，并不违背理性经济人假设。

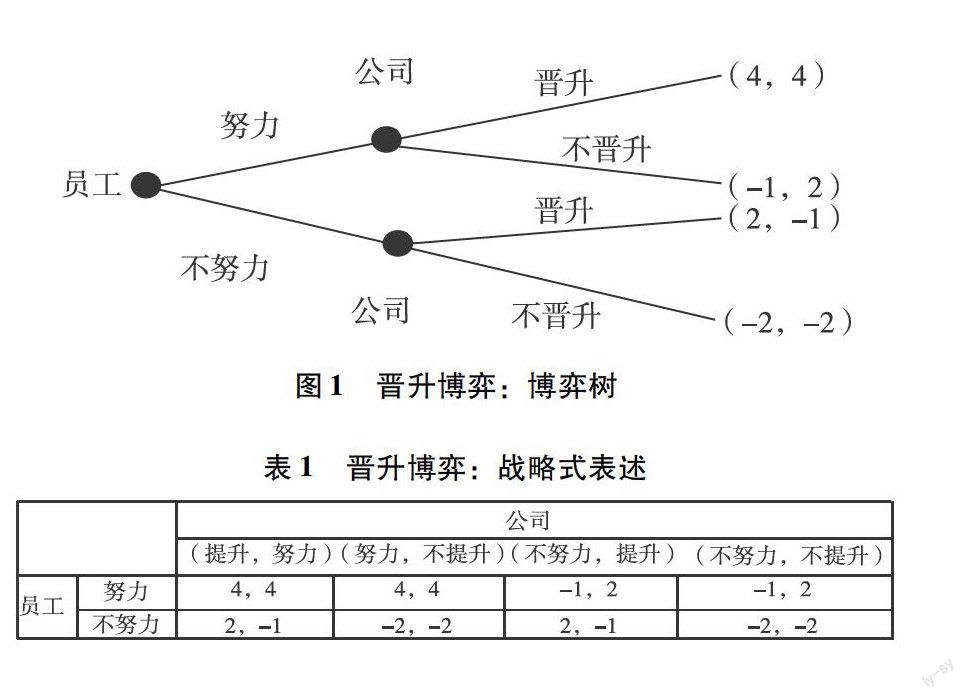
应用完全信息动态博弈来分析短期内员工的晋升博弈是指：员工（参与人1）先行动，企业（参与人2）后行动，且员工清楚自身和企业在各种情形下的收益，企业也清楚自身和员工在各种情形下的收益。假设员工可选择的行动集合是A={努力，不努力}，企业可选择的行动集合是B={晋升，不晋升}。晋升博弈的顺序：员工从其行动可选集A中选择一个行动a，企业观察到员工这一行动后从其行动可选集B中选择一个行动b。员工和企业的不同行动组合决定了二者在各自不同情形下的收益。晋升博弈的博弈树如图1所示，战略式表述如表1所示。

图1 晋升博弈：博弈树

表1 晋升博弈：战略式表述

短期内员工与企业的博弈中，员工在每个信息集上有两个选择，因而企业有四个纯战略，分别为：一是不管员工努不努力，都晋升；二是员工努力，就晋升，不努力，就不晋升；三是员工努力，就不晋升，员工不努力，却晋升；四是不管员工努不努力都不晋升。

從战略式表述中我们可以看到，在这个博弈中存在三个纳什均衡，分别为（努力，（晋升，努力））、（努力，（不晋升，努力））和（不努力，（晋升，不努力）），在每一个均衡中，给定对方的策略自身的选择都是最优的。第一个和第三个均衡结果是员工努力，企业晋升，员工不努力，企业不晋升。第二个结果是，员工努力，但是企业不晋升。

这里的纳什均衡解具有多重性，我们采用逆向归纳法提出严格劣战略，求出什么战略式表述的子博弈精炼纳什均衡。首先，员工知道企业是理性的，如果自己努力工作，给企业带来很大的经济收益，企业为了留住自己，必然会选择晋升，使双方都得到4单位的支付，而不是自己不努力，企业也不会给自己晋升的希望，此时双方都得到-2单位的支付，用博弈论的角度来说，此时纳什均衡（不努力，（不晋升，不努力）），是一种严格劣战略，因此可以进行剔除。然后，我们再看纳什均衡（不努力，（晋升，不努力））在这个均衡解中员工不努力，企业晋升，企业增加成本支出，虽然可能对员工有一定的激励作用，但自身来说确实负的效用，不是其最优的选择。因此最后一个纳什均衡（努力，（晋升，努力））是这个博弈中唯一的子博弈精炼纳什均衡。即此时存在唯一的均衡路径“员工—努力—企业晋升—（4，4）”

2 2 子博弈精炼纳什均衡

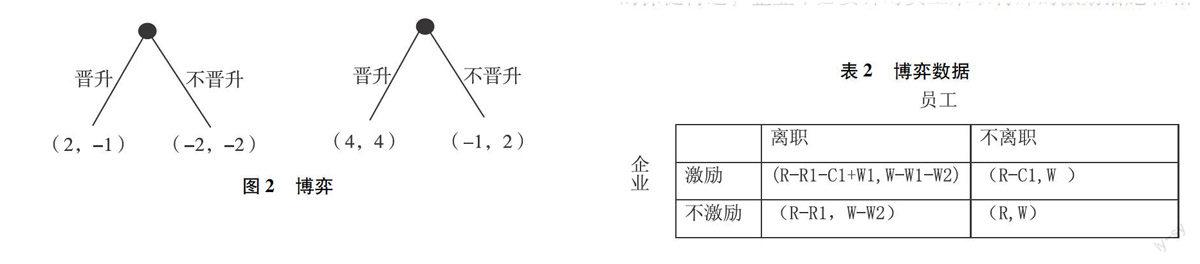
下面我们从子博弈精炼纳什均衡的定义上来（努力，（晋升，努力））是满足唯一的子博弈精炼纳什均衡的要求。从子博弈1来看，企业最优选择是晋升，达到4单位支付，子博弈2来看企业的最优选择是晋升，企业损失更小。现在让我们分析一下，上面的三个纳什均衡，是否满足子博弈精炼纳什均衡的要求，纳什均衡（不努力，（晋升，不努力））中企业的最优选择是（晋升，不努力）在子博弈2上构成纳什均衡，但是在博弈1上不是纳什均衡，再看（努力，（不晋升，努力））企业的最优选择是（不晋升，努力），在子博弈1和2都不是纳什均衡，最后我们看（努力，（晋升，努力）），即不管员工是否努力，企业都晋升实现更大的激励，带来更大的潜在收益，留住人才同时激发积极性。此时晋升是1和2上的纳什均衡，满足子博弈精炼纳什均衡的定义，因此，（努力，（晋升，努力））是唯一的子博弈精炼纳什均衡。详见图2。

图2 博弈

2 3 经济内涵

根据上述博弈过程与分析，晋升博弈唯一的子博弈精炼纳什均衡为（努力，晋升），即员工努力工作，公司给予他晋升机会，这也是为多数成熟公司所采用的晋升制度，在实践中也得到了证实。员工倾向于努力工作争取晋升机会，而公司也会满足员工的晋升需求。甚至即使员工可能工作程度努力不够，但公司出于保险起见，依然会从工龄等角度测评并对其予以晋升，因为如果公司不予晋升而导致员工的积极性下降、人力资本与知识要素在于其他公司竞争中处于劣势，从而损失更大。因此，晋升是公司的占优策略。综合起来，员工的努力、公司的晋升，二者形成良性互动，推动企业更好的长期发展。

3 中长期合同员工的完全信息动态博弈

前面我们基本分析在完全信息动态的情况下，短期雇佣员工与企业之间进行的博弈。但是企业中也存在很多的长期合同的员工，即我们所说的“铁饭碗”，这类员工与企业之间在完全信息博弈，其中长期企业先做出的激励和不激励的措施，员工根据企业是否激励选择离职或者不离职，且这类群体与企业在博弈时更多时候进行的不是单次博弈而更倾向有限次的重复博弈甚至无限次的重复博弈。

3 1 有限期合同的完全信息重复博弈的行为选择

我们首先分析，有限次的重复博弈下的长期合同员工的行为选择，现在假定企业与员工签订合同为期10年，这样博弈企业与员工之间就变成了完全信息下的10次重复博弈。此时企业先选择是否进行激励，然后员工相应做出离职或者不离职的决定，即长期中仍然假定员工的行为有两种选择即（离职，不离职）企业的行为也是两种选择即（激励，不激励）。假设员工作为博弈的参与者在的企业中能够获得的收益为W；但是员工做出离职的决定，其将面临着失去企业给予的保健因素W2；在企业采取签订合同等激励和约束措施防止员工流失的情况下，员工离职将交纳违约金W1。另外，企业激励下员工为企业创造的收益为R；而员工离职给企业带来的损失为R1；企业为防止员工流失采取的激励和约束措施，包括日常监管成本和阶段性给员工的激励，付出的成本为C1， 企业从自身角度考虑，其采取的针对员工离职倾向的约束措施必须能够弥补相应的激励成本，即 W1>C1。

如表2所示可知，博弈的纳什均衡为企业不采取激励和约束措施、员工不离职的（R，W）。表明在外部劳动力市场竞争激烈，由于企业提供给员工稳定的就业收入、和谐的人际关系以及比较适应的工作条件和良好的晋升机会等基本的保健待遇，企业不必要针对员工采取特殊的激励措施和相应的约束手段，员工队伍也将保持稳定状态。

表2 博弈数据

我们将长期的企业员工之间的博弈用博弈树进行表示，如图3所示，企业是先行者用A表示，员工用B表示。

图3 博弈数据

为了便于分析，我们对上面的支付矩阵进行定量化设计，假设R=8，R1=4，R2=3 W1=3，W=7，，C1=2，W2=2，如表3所示。

表3 博弈数据

现在我们首先分析10年合同期的有限次博弈，在这个博弈员工选择离职的唯一原因企业所给的激励措施不能满足员工的要求，使企业对自己给予更多的激励措施。但在有限次博弈中离职并不是一个可置信的威胁，因此企业最优的选择就是不激励。根据完全信息动态博弈有限次博弈原理，那么一次性博弈的子博弈精炼纳什均衡，在有限次重复博弈下其最优选择仍然是相同的。

因此，在有期限的合同中，只要企业设置较高的离职赔偿，就可以在一定程度上起到一种承诺作用，员工合同期限内离职的可能性就大大降低，从而保证企业内人员的稳定性，同时也在一定程度上降低了激励所需要的成本。

3 2 终生雇佣下的博弈的行为选择

某些企业会与员工签订终身雇佣的合同，此时这种合同实质上是企业对员工的一种承诺，改变员工在离职或者不离职的选择，此时博弈不再是企业与员工之间的博弈，而转化为这些终身雇佣制的员工之间的博弈，从理性的角度来说，团队中每个人应当都努力工作，实现企业利润的最大化同时也就实现自身的利润最大化，但是总有一些主体会采用非理性的选择，企图“搭便车”，那么在终身雇佣制的条件下，员工做出这样的选择，不会有从企业离职的威胁，但是会导致其他员工采取相同的策略，最终企业的经济收入不断下降，大家都会被离职，因此在终身雇佣制下的激励，更多时候是如何实现团体合作之间的更好的激励，从而才能实现企业的更好的发展。

现在我们结合无限次重复博弈下的囚徒困境下，终身雇佣制员工的囚徒困境的子博弈精炼纳什均衡。详见表4。

囚徒困境模型表明在完全信息情况下短期博弈中参与人会选择不合作行为，但是在无限次重复博弈模型中，参与人有可能为了长期利益而选择合作行为，虽然合作行为并非参与人的单期最优战略。在无限次重复囚徒困境博弈中如果参与人选择冷酷战略，就有可能使得合作作为纳什均衡出现。该冷酷战略是：开始选择抵赖，直到有一方选择了坦白，然后永远选择坦白。根据这个战略，一旦一个囚徒在某个阶段博弈中自己选择了坦白，他以后将永远选择坦白。假设囚徒 B 选择冷酷战略，则可证明囚徒 A 选择冷酷战略也是最优的。令δ为贴现因子，并假定两人的贴现因子相同。如果 A 在博弈的某个阶段选择了坦白，他在该阶段得到0 单位的支付，而不是-1 单位的支付，因此他的当期尽支付为 1 单位。但是他的这个机会主义行为将触发囚徒 B 永远坦白的惩罚，因此 A 随后每个阶段的支付均为-8 单位。因此如果下列条件满足，给定 B 没有选择坦白，A 将不会选择坦白。

表4 数据

0-8δ-8δ2-8δ3-…≤-1-δ-δ2-δ3-…

即-8δ1-δ≤-11-δ

解得，δ≥18。当δ≥18时，给定B选择冷酷战略并且没有首先选择坦白，则A不会首先坦白。

通过上面的分析，我们发现当企业与员工之间签订终身雇佣制合同时，增加员工的稳定性，将企业和员工叠加在一起，此时企业内博弈就不再是企业与员工之间博弈，而是转变为员工之间团体合作的博弈，在无限次重复博弈的条件下，理性的员工必然都会选择努力工作，更有效地调动员工工作的积极性和员工对企业的忠诚度。

4 结 论

综上我们对三种合同期限的员工与企业之间如何进行博弈进行分析，短期临时合同下，由于员工先选择努力工作或者不努力工作，企业在选择是否进行晋升，其均衡的子博弈精炼纳什均衡是，（晋升，（努力，晋升）），因此在短期临时情况下，员工只有通过努力工作，从可以获得更大的晋升可能性，因为此时主动权在企业手中，企业面临的成本相对较小，在有限的合同下的重复博弈，此时员工对企业的整体激励已经理解，因此根据企业的行为作出自己的最优选择，而此时对于企业来说，可以通过设置较高的违约成本抑制员工的离职，而在终身雇佣制的条件下，就不再是企业与员工之间的博弈，而转化为员工团队之间为一个目标的博弈，最终推动企业的发展。因此对于不同的员工企业应当选择合适的激励和约束措施，从而更好实现双方利益的最大化。

参考文献：

[1]蒲勇健，赵国强 内在动机与外在激励[J].中国管理科学，2003（5）

[2]张嫘 企业员工积极性激励方法分析选择[J].经济师，2003（1）