利用MATLAB计算AP1000可靠性数据的初步探索
王瑛 关高
摘 要:可靠性数据分析为核电厂设备的可靠性试验和可靠性维修等可靠性管理工作提供决策依据,在可靠性工程中占有重要地位。该文以AP1000的DTS泵为例,初步探索了AP1000电站设备可靠性数据的采集与处理、可靠性参数的分析计算这一过程。对于可靠性数据的计算,本文在行业通用数据及电站专有设备运行数据的基础上,利用Matlab平台实现了经典概率统计和贝叶斯估计两种方法的算法,摸索出一套可行的可靠性数据分析体系,引领AP1000电站设备可靠性数据分析工作的开展。
关键词:失效率 可靠性数据 MATLAB 贝叶斯估计 AP1000
中图分类号:TL353.13 文献标识码:A 文章编号:1674-098X(2015)03(a)-0033-04
可靠性数据是系统可靠性设计、研究、分析、评定和改进的基本依据,数据分析则是可靠性工作的基础。通过有计划、有目的地收集和分析系统各组成单元的可靠性数据,可定量评定系统的可靠性水平,发现其可靠性的薄弱环节和产生原因,经过改进,使系统的性能与可靠性水平不断提高。
核电厂使用的设备可靠性参数一般为以下四种:设备的运行失效率λ,设备的需求失效概率γ,设备的平均故障维修时间τ,设备由于维修及试验形成的设备总不可用度P。因篇幅和数据所限,该文的计算集中在前两个数据。
可靠性数据的计算和分析,涉及较多概率统计和高等数学计算,较为复杂和繁重,难以人工计算,可靠性数据分析普遍借助专用定制软件完成。MATLAB的统计工具箱是建立在MATLAB数值计算环境上的工具集,具有保证可靠性数据分析工作及时、准确、直观简便完成的能力。该文以全球首堆的AP1000工程的DTS的清水泵为例,利用MATLAB这一在工程上得到普遍应用的数学软件,实现了可靠性数据的核心计算过程。
1 设备基础信息
1.1 设备类及设备选取
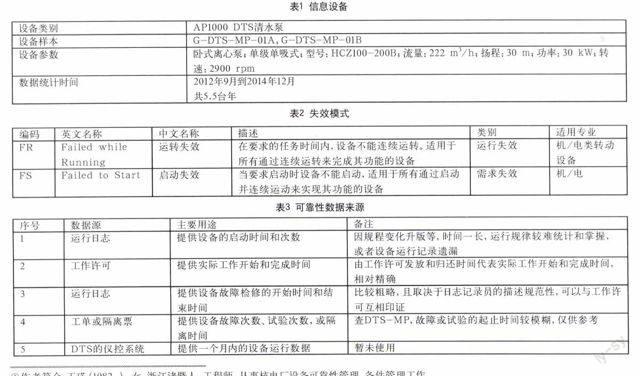
设备可靠性数据的计算均基于设备类进行。一个设备类表示具有相似的工艺性能、相似的功能和相似的运行条件的一组设备。多数情况下,一个设备类相当于一组明确的设备组合,如该文的DTS清水泵类。下表列出了该设备类的基本信息(表1)。
1.2 设备边界
设备边界是可靠性数据库的一个重要属性。定义设备边界主要是为了提高设备失效历史数据的采集质量,同时,设备边界的划分也会影响到设备的失效模式。
该文所涉的DTS清水泵的边界为泵的进出口接管嘴,以法兰或焊缝为分界点。主要装置包括泵本体、润滑装置、冷却装置、以及相应的传动装置,不包括电动机。主要零部件包括泵壳、泵轴、泵轴承、叶片、冷却设备、润滑设备、联轴器。
2 设备失效模式
失效模式是设备失效的表现形式。失效模式可采用多种分类方法。为规范化和标准化,该文将设备的失效模式分为两大类:其一为运行失效,即设备在运行期间或备用期间发生的失效;其二为需求失效,即设备在状态变换时刻发生的失效。表2为基本失效模式定义描述详表。
2.1 设备运行和失效数据
2.1.1 数据源
表3列出了三门核电设备可靠性数据的来源和用途。
2.1.2 清水泵运行数据分析
表4对DTS清水泵的运行数据进行了详细的收集和整理。
综上,清水泵累计投用小时数为19680 h,净运行小时数为1010.35 h,累计启动次数为1354次。
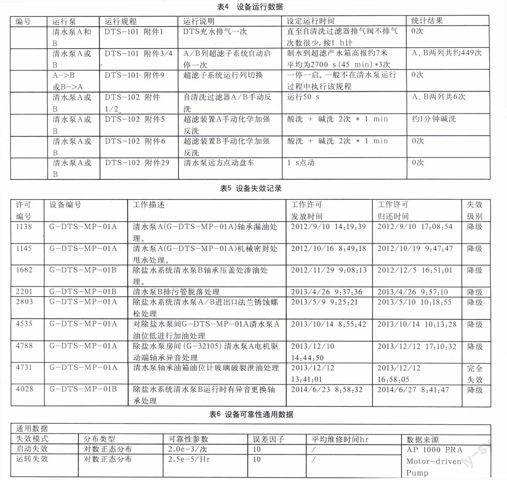
2.1.3 清水泵失效数据分析
清水泵完全失效的标准包括:要求时不启动、非计划停泵、严重外漏、性能丧失、冷却丧失、卡住、卡轴、丧失润滑。
清水泵性能降级的标准包括振动、渗漏油、甩水、异音、油位低、辅助管件脱落、锈蚀等。
表5为清水泵失效记录
综上,清水泵累计运转失效次数为1次,平均维修时间为3.3 h,累计启动失效次数为0次。
3 设备可靠性参数的经典估计及Matlab实现
3.1 大样本空间下的经典估计
经典估计对大样本空间下的可靠性参数估计效果很好。当设备失效样本充分时,Matlab的经典估计按如下步骤进行。
绘制可靠性数据分布的频数直方图。失效概率密度的形状与频数直方图一致,因此可以直观假设可靠性数据服从的分布。Matlab工具箱提供hist(data,k)函数用于作频数直方图。
参数估计。根据直方图的形状,假设可靠性数据服从负指数分布。指数分布可用[muhat,muci]=expfit(data)进行参数估计,该命令用极大似然法完成指数分布的点估计和区间估计。
假设检验,观测样本数据的分布与选定的理论分布之间符合程度。通用的拟合优度检验有2检验和柯尔莫哥洛夫检验。后者可用[H,P,KSSTAT,CV]= kstest(X,cdf,alpha)命令完成。
国外主要的通用设备可靠性数据库的先验分布均来源于大样本空间下的经典估计。
3.2 运行失效率λ的小样本经典估计
设备的运行失效率λ(t)是指在t时刻,残存的Nt台设备在单位时间dt内发生失效的次数dN与残存设备数量Nt的比值,即λ(t)=dN/(Ntdt)。因单体电厂失效样本空间小,难以采用大样本空间的经典估计,因此在经典估计过程中普遍进行小样本估计。根据以往的经验,与国际上对核电厂设备失效的通用做法,在小样本空间下,可假设电厂中设备的寿命服从指数分布,即假设失效率与t无关,保持恒定。
在该前提下,设备运行失效率的点估计:
运行失效率λ=n/T,n=所观察到的运行失效次数、T=设备的累计运行时间。
没有观察到任何一个运行失效的特殊情况,也就是设备的运行失效次数n为0时,根据“2(Khi-2)在50%的规则”,= 250%(2n+2)/2T 1.39/2T 0.7/T
对参数λ的误差因子EF则根据下式计算:
EF=(P上界值/P下界值)0.5
上界值、下界值分别对应95%、5%置信度的值,可由2函数计算。当n为0,下界值为0时,EF取10。
上述算法的Matlab代码如下。其中,求解2函数等于0.95或0.05时的x值这一高等数学计算,在matlab平台通过chi2inv函数就能轻松计算(图1)。
综上,计算可得清水泵的运行失效率为5.0813e-5/H,EF为9.62。值得注意的是,一般而言,只有当设备类的累计运行数据至少等于所对应通用数据的倒数时,且设备类的累计失效次数不少于2次,经典估计方法计算出的电站特有数据才可以使用。
3.3 需求失效概率γ的小样本经典估计
设备需求失效概率γ是指要求设备变换状态(如要求打开、关闭、启动、停机等)时发生失效的概率。在假设电厂中设备的需求失效概率γ与t无关、保持恒定时,需求失效次数服从二项式分布。二项式分布描述了在Ns次独立重复试验中,发生n次故障的概率分布。与指数分布为连续型概率分布不同,二项式分布为离散型概率分布,其他性质与指数分布相似。因此,相关参数与运行失效率的算法类似,简单列示如下:
当n=0时,γ=0.7/Ns=0.7/1354= 5.1699e-4/次
当n=0时,EF=10
4 设备可靠性参数的贝叶斯估计及其Matlab实现
4.1 先验通用数据选取
贝叶斯估计是综合经验信息进行可靠性评估的方法,与经典统计既相互竞争,又相互支持、共同发展。贝叶斯方法假设可靠性指标有一个根据历史资料和经验信息确定的先验分布,根据先验分布和后期观测数据导出后验分布,并从后验分布得出可靠性指标,包括点估计和区间估计。
贝叶斯估计的特点就在于先验分布。由于有了先验分布,不需要很大的样本就可以得到较好的估计,这是贝叶斯方法的最大优点。但同时,如何在多种先验中选取符合实际的分布,缺乏一个较好的、统一的方法。
核电行业目前在国内还缺少具有行业认可度的可靠性数据库,但可选作先验的国外的数据库已较多,比较知名的有:基于法国核工业的欧洲可靠性数据银行、基于日本核工业的WANO核设备可靠性数据系统、基于瑞典核工业的IAEA的用于PSA的设备可靠性数据等。三门核电作为AP1000堆型全球首堆项目,设计院西屋公司的PSA报告提供了基于美国运行电站的可靠性数据,包括设备分类、失效模式及通用设备失效率,在该报告中,假定所有设备的失效分布为对数正态分布。该文的贝叶斯估计将AP1000的PSA可靠性数据用作先验分布,其中电机泵的通用数据如下,见表6。
4.2 运行失效率λ的贝叶斯估计
因伽马分布具有两个参数、的调节,适用范围很广,且在数学上处理方便,被广泛用作可靠性数据的后验分布。当为1时,伽马分布就是参数为的指数分布;当为正整数时,伽马分布可以看做个独立的指数分布之和;当趋向较大数值时,伽马分布则近似于正态分布(n个同分布的独立变量服从正态分布)。
因先验分布为对数正态分布,本文将通过以下步骤求取后验分布参数及运行失效率。
已知先验对数正态分布的均值和EF,求得对数正态分布的参数、和95%分位点。
因对数正态分布的EF=exp(1.645)[4],可得=lnEF/1.645。
根据对数正态分布的均值λ=exp(+ 2/2),可得=lnλ-2/2。
已知对数正态分布的参数后,可求得95%分位点为9.3842e-005。
Matlab代码如图2:
将先验对数正态分布转换为伽马分布,使得这两种分布在均值和95%分位点这两个关键点上重合。也就是说,已知先验伽马分布的均值和95%分位点,求伽马分布的参数、。
该问题可转换为求解如下方程组[3]:
=伽马分布的均值=先验对数正态分布的均值λ
该方程组的数学方法解极为复杂,但在Matlab平台用数值方法却不难解决,通过下面的代码,可以得到先验参数为0.534,为4.6816e-005(图3)。
在上述先验伽马分布的参数的基础上,根据设备运行和失效数据,求得后验伽马分布。
伽马分布为共轭型先验分布,因此后验分布同为伽马分布。其后验参数分别为[3]:
B = +n
B = /(T+1)
λB = (+n)/(T+1)
其中,n=所观察到的运行失效次数,T=设备的累计运行时间。
因此,B=1.5340,B=2.4366e-005,λB =3.7378e-005/H。
4.3 需求失效概率γ的贝叶斯估计
需求失效的似然函数为二项式分布,共轭型先验分布为贝塔分布。因先验分布同样为对数正态分布,求取后验分布参数及需求失效概率γ的步骤与运行失效率的算法相同,即:
已知先验对数正态分布的均值2.0E-3和失效因子10,求得对数正态分布的参数=1.3997,=-7.1943,95%分位点= 7.5e-3。
将先验对数正态分布转换为贝塔分布,使得这两种分布在均值和95%分位点这两个关键点上重合。也就是说,已知先验贝塔分布的均值和95%分位点,可利用Matlab求得贝塔分布的参数=0.53,=264.47。
在上述先验贝塔分布的参数的基础上,根据设备需求次数和失效数据,求得后验贝塔分布,其后验参数分别为[3]:
B=+n
B=+Ns-n
λB=(+n)/(++Ns)
其中,n=所观察到的需求失效次数,Ns=设备的累计需求次数。
因此,B=0.53,B=1.6185e+003,λB= 3.2736e-004/D。
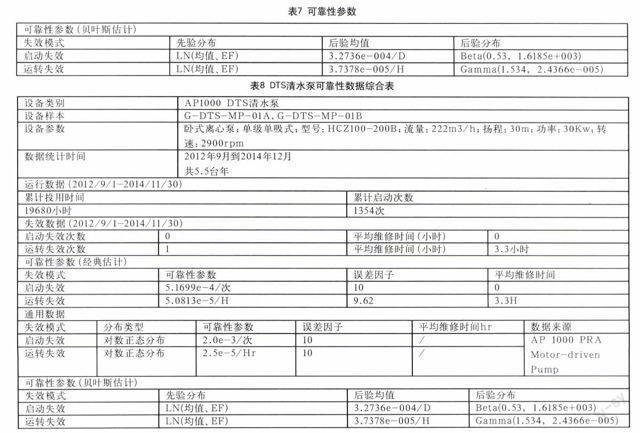
综上,形成可靠性参数如表7。上述算法全部用AP1000的PSA数据检验通过。
4.4 可靠性数据综合表
DTS清水泵可靠性数据综合表见表8。
5 用Matlab进行可靠性数据分析的意义
随着可靠性、维修性工作的深入开展,可靠性数据分析工作越来越显示出其重要的价值和作用。可靠性数据分析为核电厂设备的可靠性试验和可靠性维修等可靠性管理工作提供了决策依据。借助有计划、有目的地收集设备生命周期中的数据,经过有目的的分析,发现电厂设备的重要性和薄弱环节,并利用这些重要信息采取相应的应对措施,改进设计、提升维修策略、改善试验计划、保障备件等,达到最终提升电站设备可靠性的目的。
Matlab这一工程通用数学软件,内置统计工具箱,借助这一平台,可靠性管理工程师可以直观简洁地绘制可靠性分布的图形、产生符合相应规律的随机数据等,加快相关人员对可靠性数据和分析过程的理解和掌握。
Matlab计算准确,在工程计算领域得到广泛的检验,利用Matlab计算的标准正态分布表值、卡方分布表值等,全面符合国家标准,本文的算法,也全部通过欧洲可靠性数据银行等通用可靠性数据进行了验证。
最重要的是,Matlab应用广泛,常用算法代码开源且标准化,如常见插值、函数逼近、解线性方程组的迭代法等算法,均有标准代码实现,借助Matlab,常常使用一两个函数就能解决复杂的统计计算过程,使可靠性数据分析过程高度工程化、平民化,保障可靠性数据分析工作及时、准确、直观简便地完成,促进了电厂可靠性数据分析工作的开展,提高了核电厂设备可靠性管理工作的科学性和定量程度。
参考文献
[1] 赵皓.秦山第二核电厂设备可靠性数据库的研究和开发[D].上海交通大学,2008.
[2] 内部资料.三门核电一期工程1&2号机组概率安全评价.SMG-PRA-GL-001.
[3] Henri Procaccia,Spyros P.Arsenis,Patrick Aufort. EUROPEAN INDUSTRY RELIABILITY DATA BANK[M].Crete University Press, 1998.
[4] Reliability and Preventive Maintenance:Balancing Risk and Reliability.EPRI,Palo Alto, 2002.1002936.
[5] 苏林军.MATLAB在可靠性数据分析中的应用[J].煤矿开采,2007(2).
[6] 赵宇,杨军,马小兵.可靠性数据分析教程[M].北京航空航天大学出版社,2009.
[7] 贺国芳,孙芳.现场可修系统的可靠性数据处理[J].北京航空航天大学学报, 1995(8).