基于四步相移光栅投影的三维形貌测量系统

尚忠义，李伟仙，董明利，段良君

（北京信息科技大学 光电测试技术北京市重点实验室，北京100192）

引言

基于光栅投影测量方法［1－6］是近年来发展起来的具有代表性的一种三维视觉技术。这种测量方法具有非接触、成本低和精度高等优点，广泛应用于光学三维测量领域。在数字光栅投影测量方法中最为常用的算法是相移算法［2－6］。近年来，在条纹投影的三维形貌测量研究中，有跳变面物体的形貌测量，一直是该技术的研究热点之一［1－3］。有采用多频条纹投影结合傅里叶变换或时间相移技术，研究跳变面对相位解调影响的问题［11－14］。然而在单色投影的情况下，需要采集多幅、多频条纹图，之后再解包裹，得到连续相位。另外，傅里叶变换中的频谱混叠是影响相位求解的最重要的因素，傅里叶变换法不适合处理几何形状复杂的物体，尤其有跳变面的物体，当物体边界有较大突变区域时，傅里叶变换法求的相位误差比较大，进而对物体三维形貌的重建及测量有影响。因此，本文采用相移法对物体进行三维形貌重建。相移法是通过对条纹进行相移来获取多个具有不同初相位的条纹图，结合多幅条纹图能够得到位于［－π，＋π］范围的主相位值。相移法具有高分辨率、高精度、算法简单和处理速度快等优点［1－3］。利用相移法测量过程中，在求解相位时要利用反正切函数求解得到相位值，但这些值只是被测物体表面对应点的实际相位在2π主值区间内的值，即［－π，＋π］范围内的截断相位的包裹相位，与其对应点的实际相位差2π的整数倍，求解真实相位值的过程通常称为相位解包裹，或称相位展开。目前，应用相移法测量有跳变面物体形貌时，一般常用的相位展开法有时间相位展开法［15］、灰度编码法［16］、多频相位展开法［4］和双频光栅法［1］等。上述方法测量在三维形貌重建时，需要至少投影和采集6幅条纹图，影响了测量的速度。本文提出了一种新的适合于有明显跳变面物体形貌测量的四步相移法，测量只需要4幅正弦条纹图就能获得可靠的连续相位图，缩短了相移法的测量时间，提高了测量速度。

1 光栅投影测量系统的构成及其工作原理

1.1 光栅投影测量系统硬件构成

图1为光栅投影测量系统硬件构成图。光栅投影测量系统由投影仪、CMOS相机、计算机等3部分组成。此系统首先对系统进行标定，而后通过PC计算机编码正弦条纹图案，由LCD投影机投影4幅正弦条纹图，由CMOS相机获得被调制的图案，之后通过软件进行测量。

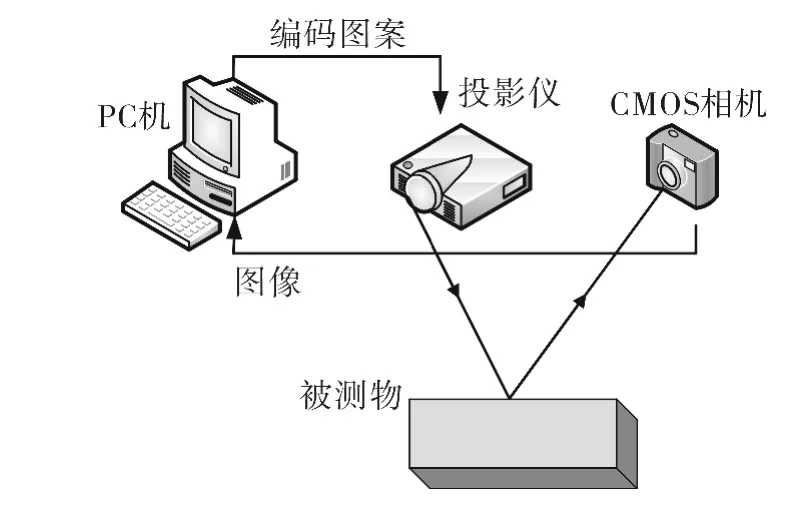
图1 光栅投影测量系统硬件构成图Fig.1 Hardware configuration of grating projection measurement system

1.2 光栅投影测量系统工作原理

该光栅投影测量系统首先通过计算机编码正弦条纹图案，然后通过投影仪投射出来，投射4幅正弦条纹图像，而后CMOS相机采集到4幅图像被调制的图像，接着图像被传输给计算机，计算机通过软件进行测量，具体工作流程如图2所示。

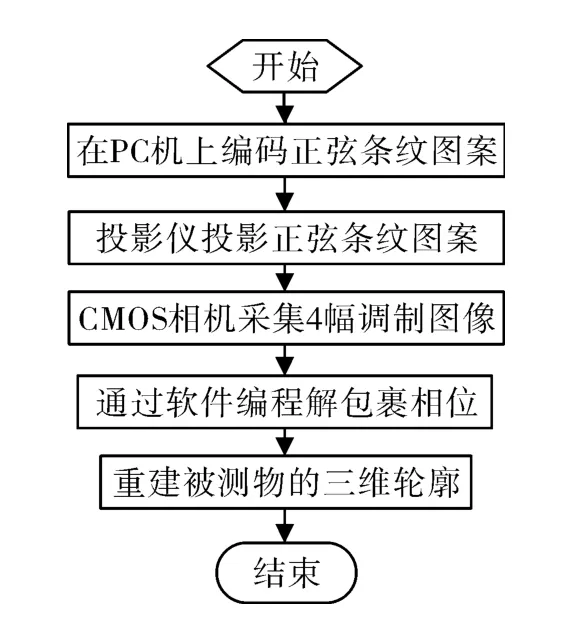
图2 系统工作流程图Fig.2 System working flow chart

2 光栅投影测量系统软件的关键算法

2.1 四步相移相位测量原理

由于本系统是基于四步相移光栅投影的三维形貌测量系统，因此在这里只介绍四步相移法相位测量原理。数字相移正弦光栅由计算机编码产生并投影到漫反射的物体表面时，CMOS相机采集的反映物体表面高度的被调制条纹的灰度可表示为（通过软件依次生成4幅相移为π／2的图像，并且由投影仪投影出来）

（1）式～（4）式中：A（x，y）为背景光强；B（x，y）为物体表面的反射率；f为光栅条纹的空间频率；φ（x，y）为被截断在（－π，＋π］的相位主值。即使条纹图灰度表达式中A（x，y）与B（x，y）不是常数，但对于静态测量各个测点处的值是不变的，因此由（1）式～（4）式，可得：

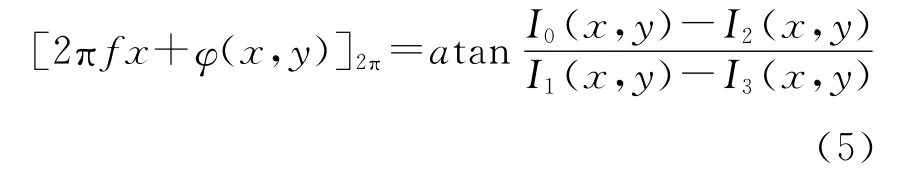
即可得到2πfx＋φ（x，y）的包裹相位。（5）式左端的下标2π表示方括号内的值对2π取余，然而［2πfx＋φ（x，y）］的真实相位值需要通过相位去包裹技术进行还原。得到二维全场的［2πfx＋φ（x，y）］连续相位值后，减去载波相位（即代表参考平面的相位2πfx），即可得到反映物体表面三维形貌信息的相位φ（x，y）。

2.2 明显跳变面测量算法

对于表面连续并且没有明显凹陷或跳变的被测物，不存在阴影的问题，即当得到包裹相位后，进而进行解包裹可得到连续的相位，这样可精确地进行三维重建。然而，在测量过程中，总会有一些被测物表面有跳变或有明显凹陷或突起。条纹投影时会产生阴影或条纹中断的现象，在这种情况下，如果还继续采用四步相移法计算相位，直接运用相位解包裹技术无法得到准确的连续相位图，而得到的相位在阴影区存在尖锐的毛刺信号或不正常的跳跃。

为了解决上述问题，要确定有明显跳变区域和阴影的区域。本文用二值化方法对有明显跳变和阴影区域进行定位提取，具体方法：将4幅相移图相加求和，而后除以4得到平均灰度图，则有

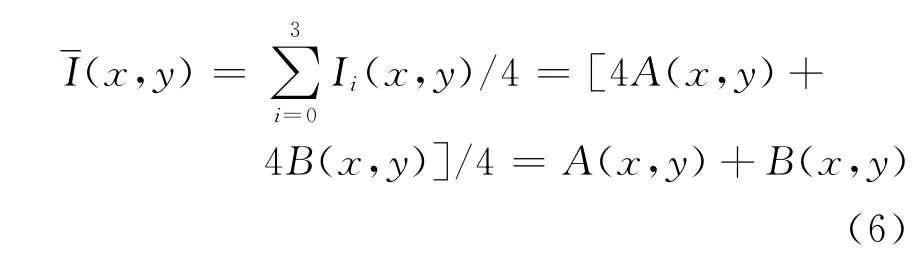
2.3 重建算法流程图

光栅投影测量系统的重建算法流程图如图3所示。首先，通过对4幅相移图算术求和并除以4得到平均灰度图；接着，将平均灰度图二值化处理定位明显跳变面或阴影部分；最后，将二值化图像与包裹相位图卷积，而后对包裹相位图进行解包裹，从而得到正确的连续相位，重建被测物的三维轮廓，见图3所示。

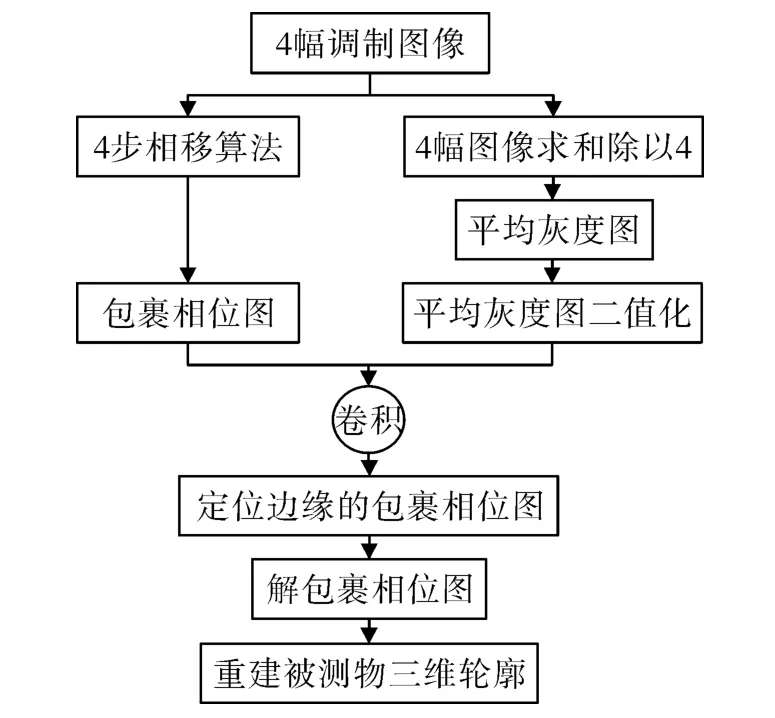
图3 系统重建算法流程图Fig.3 Flow chart of system reconstruction

3 测量实验与结果

3.1 系统标定

在测量前对实验仪器进行系统标定。首先，使用张正友棋盘格标定方法标定摄像机内外参数，像素对应的平面实际尺寸可以由此标定方法得到，此处不作详细说明。然后，使用在表面喷涂一层薄漆的金字塔正四棱锥做三维靶标，见图4所示。由于解包裹得到的连续相位的大小和正四棱锥的高低成线性关系，那么设四棱锥的高为H，解包裹得到的最大相位为Φ，得到Z轴方向的标定量K＝Φ／H，这样相位大小和Z轴方向的实际尺寸就能对应起来，完成系统标定。

图4 金字塔正四棱锥靶标Fig.4 Rectangular pyramid target

3.2 实验结果

在实验中，正弦条纹由爱普生EB－C50W型号LCD投影仪投影得到，投影条纹周期为21pixel／条。采集采用CatchBEST凯视佳的MU3C500M／C（MRYY0）型号的CMOS相机，该相机有效像素为500万像素。系统实物图如图5所示。测量过程：首先进行系统标定，然后将4幅相移图作为标准参考面，通过相机采集图像，图6（a）是相机采集的其中一幅带有条纹的参考平面，通过（5）式计算得到“包裹”相位，再直接应用相位去“包裹”技术得到图6（b）标准参考面的连续相位图。在参考平面上放置被测物（该被测物是一个具有2个明显跳变面的三棱锥橡皮块），再进行相移条纹投影，同时用相机进行采集，结果如图7所示；将上述4幅相移图相加，而后除以4得到如图8所示的平均灰度图；图9为平均灰度图二值化后的图像；图10是图9与包裹相位相卷积的相位图；图11即为带有被测物相位图解包裹后获得的连续相位图减去参考平面解包裹后获得的连续相位图得到的最终解包裹相位图；图12为其三维相位展示。

图5 系统实物图Fig.5 Real system setup

图6 正弦条纹的参考平面Fig.6 Reference plane of sinusoidal fringe

图7 四步相移正弦条纹投影在橡皮块上Fig.7 Four－step phase－shift sinusoidal fringe projection on rubber

图8 四步相移条纹的平均灰度图Fig.8 Average gray image of four－step phase shift stripe

图9 橡皮块二值化灰度图Fig.9 Binary gray image of rubber

图10 二值化灰度图与包裹相位图卷积后相位图Fig.10 Phase map with convolution of binary gray image and wrapped phase map

图11 橡皮块的连续相位图Fig.11 Continuous phase diagram of rubber

图12 橡皮块的三维相位分布图Fig.12 Three－dimensional phase distribution of rubber

3.3 误差分析

对上述被测物（三棱锥橡皮块）的体积进行多次测量，表1给出了测量5次的结果和相对精度。

表1 测量三棱锥橡皮的体积及其相对精度Table 1 Triangular pyramid rubber volume measurementand it's relative accuracy

经过5次测量被测物体积的相对精度在2%以下，5次测量被测物体积均值相对于被测物实际体积的相对误差为0.47%，验证了此文算法的有效性。

4 结论

本文采用四步相移法，通过对4幅相移图求算术和而后除以4得到其平均灰度图，根据平均灰度图中反映被测物灰度与参考平面灰度差异，将平均灰度图二值化，可准确定位有跳变面和阴影区域，而后将平均灰度图二值化得到的结果与带有被测物的包裹相位相卷积，而后再解包裹。此方法避免了传统四步相移的在计算及解包裹过程中由于阴影的存在导致很多毛刺信号以及遇到明显跳变面相位解包裹时对条纹级数的误判而出现的误差。同时也避免了双频以及多频相移测量过程中需要投影和采集多幅条纹图，有效减少了测量时间和图像存储空间，提高了三维形貌测量的效率。实际测量表明该方法用于体积测量的平均相对精度为0.47%。

［1］ DaiI Meiling，Yang Fujun，He Xiaoyuan.3－D shape measurement of objects with discontinuities by dualfrequency color fringe projection［J］.Optics and Precision Engineering，2013，21（1）：7－12.戴美玲，杨福俊，何小元.基于双频彩色光栅投影测量不连续物体三维形貌［J］.光学精密工程，2013，21（1）：7－12.

［2］ Zheng Dongliang，Da Feipeng.Double－step hase－shifting algorithm for fringe－projection measurement［J］.Acta Optica Sinica，2012，32（5）：86－92.郑东亮，达飞鹏.双步相移光栅投影测量轮廓术［J］.光学学报，2012，32（5）：86－92.

［3］ Yang Fujun，Geng Min，Dai Meiling，et al.3Dshape measurement of discontinuous objects based on single frequency fringe projection in 4－step phase shifting profilemetry［J］.Journal of Optoelectronics·laser，2012，23（8）：1535－1538.杨福俊，耿敏，戴美玲，等.基于单频四步相移条纹投影的不连续物体三维形貌测量［J］.光电子·激光，2012，23（8）：1535－1538.

［4］ Huang S，Zhang Z，Zhao Y，et al.3Dfingerprint imaging system based on full－field fringe projection profilometry［J］.Optics and Lasers in Engineering，2014，52：123－130.

［5］ Pinit P，Umezaki E.Digitally whole－field analysis of isoclinic parameter in photoelasticity by four－step color phase－shifting technique［J］.Optics and Lasers in Engineering，2007，45（7）：795－807.

［6］ Pan B，Kemao Q，Huang L，et al.Phase error analysis and compensation for nonsinusoidal waveforms in phase－shifting digital fringe projection profilometry［J］.Optics letters，2009，34（4）：416－418.

［7］ Huang P S，Zhang S.Fast three－step phase－shifting algorithm［J］.Applied Optics，2006，45（21）：5086－5091.

［8］ Ren Tongqun，Zhao Yuehan，Gong Chunzhong，et al.Unconstrained registration of 3－D scattered point clouds for free－form shape measurement［J］.Optics and Precision Engineering，2013，21（5）：1234－1243.任同群，赵悦含，龚春忠，等.自由曲面测量的三维散乱点云无约束配准［J］.光学精密工程，2013，21（5）：1234－1243.

［9］ Xie Jieru，Cui Haihua.Study on four－step phase－shifting decoding algorithm for three－dimensional profilometry［J］.Acta Optica Sinica，2009，29（2）：370－373.谢捷如，崔海华.面向物体表面测量的四步相移光解码技术研究［J］.光学学报，2009，29（2）：370－373.

［10］Jiang Hongzhi，Zhao Huijie，Liang Xiaoyue，et al.Phase－based stereo matching using epipolar line rectification［J］.Optics and Precision Engineering，2011，19（10）：2520－2525.姜宏志，赵慧洁，梁宵月，等.基于极线校正的快速相位立体匹配［J］.光学精密工程，2011，19（10）：2520－2525.

［11］ Wong Jiawen，Zhong Jingang.Application of gabor transform to 3Dshape analysis［J］.Acta Photonica Sinica，200 3，32（8）：993－996.翁嘉文，钟金钢.加窗傅里叶变换在三维形貌测量中的应用［J］.光子学报，2003，32（8）：993－996.

［12］Sun Ping，Zhang Li，Tao Chunxian.3－D shape measurement with fourier transform based on LCD projector［J］.Acta Photonica Sinica，2005，34（8）：1250－1252.孙平，张丽，陶春先.基于LCD数字投影技术的傅里叶变换法测量物体三维形貌［J］.光子学报，2005，34（8）：1250－1252.

［13］Wu Shuangqing，Zhang Yin，Zhang Sanyuan，et al.Analysis of 3－D measurement system and coordinates calibration in fourier transform profilometry［J］.Acta Optica Sinica，2009（10）：2780－2785.吴双卿，张引，张三元，等.傅里叶变换轮廓术物体三维形貌测量的系统分析及其坐标校准方法［J］.光学学报，2009（10）：2780－2785.

［14］Wang Luyang Da Feipeng.3－D shape measurement technique based on complementary color－encoded fringe projection［J］.Acta Optica Sinica，2011，31（6）：106－112.王露阳，达飞鹏.基于互补色编码条纹投影的三维形貌 测 量 方 法 ［J］.光 学 学 报，2011，31（6）：106－112.

［15］Huntley J M，Saldner H.Temporal phase－unwrapping algorithm for automated interferogram analysis［J］.Applied Optics，1993，32（17）：3047－3052

［16］Wang Z，Du H，Park S，et al.Three－dimensional shape measurement with a fast and accurate approach［J］.Applied optics，2009，48（6）：1052－1061.

［17］Zhang Z Y.A flexible new technique for camera calibration［J］，IEEE Trans.Pattern Anal.Mach.Intell，2000，22（11）：1330－1334.