基于诱思探究学习的高中数学课堂教学设计

孙月春

（大连开发区第十高级中学，辽宁 大连 116600）

数学课堂，尤其是到了高中阶段的数学课堂，进入到了抽象的数字和符号为主的学习阶段，很多学生因此产生了抵触和消极的学习情绪。我们知道，教学过程“是现实地生成与开展教学的过程”[1]，课堂是教与学关系开展的主阵地，它承载和体现着教师的教育教学基本理念，也最终决定着教育教学效果的好坏。那么，如何能够让学生在学习过程中产生兴趣，变抽象为形象，变被动学习为主动学习呢？这是笔者经常思考和关注的一个问题。

在长期的教育教学实践中，笔者发现，将“诱思探究”教学模式融入高中课堂教学设计中，会使高中数学课堂有一个“质”的飞跃。那么，什么是“诱思探究学习”呢？又如何运用到高中数学的课堂教学过程中去呢？笔者将以高中数学教学中“指数函数与对数函数的关系”这一堂课为例，来具体分析。

一、诱思探究学习理论概述

诱思探究，就是诱导思维，探索研究。“诱思探究学习”是在教育教学改革过程中涌现的一种基于“情境激疑——诱导探究——迁移运用——检查反馈”教学模式与方法下的学习模式。由陕西师范大学教育科学所张熊飞教授提出的“诱思探究教学”模式认为：（1）教师引导作用的精华归结为“循循善诱”，“诱”字是其外在表现形式的集中表达，教师引导作用的要害就是要“教贵善诱，教贵善导”，这也是发挥教师引导作用的精华。（2）使学生真正地“学”是“教”的真正含义，学生要学会全身心投入到整个教学过程，学会自己去领会、理解所学知识，“学者，所以体验、探究、创新也”。[2]

笔者所在学校进行了“诱思探究”实验研究与学习，并在学科教学中运用“诱思探究学习”理论为指导进行教学。“诱思探究学习”的实现方式对学科教学的应用价值较大，图1可以反映这一过程的本质。[3]

二、“指数函数与对数函数的关系”诱思探究课堂教学设计

结合“诱思探究教学”模式，根据高中数学的教学特点，以高中数学教学中“指数函数与对数函数的关系”这一内容为例，对课堂教学进行了如下的整体设计。

（一）情境设计，导入新课

师生之间正是通过创设的教学情境促进认知、情感、能力的发展。通过情境设计调动学生的知情意行等多方面因素，可以激励学生进行自主学习活动。“以境育情”对数学学科教学有着重大的实践意义，可以变抽象为形象，变复杂为简单，提高学习效果。在“指数函数与对数函数的关系”课堂中，设计“租房子”的故事情境开头——“带孩子的父母”与“带父母的孩子”，谁能租到房子？

一对年轻的父母带着孩子进城打工，着手租房子以备落脚。可是，找了很长时间，房主都以孩子会弄脏、弄坏房间的墙壁家具为由拒绝了——“我们不租给带孩子的住户！”父母很伤心，没有办法。这时候，孩子走到了房主面前，小心翼翼地对房主爷爷说：“爷爷，爷爷，我没有孩子，只带了两个大人，您能把房子租给我吗？”房主被可爱又聪明的孩子打动了，痛快地把房子租给了一家人。

通过这个故事给学生以形象的感受，“倒过来、反过来”思考问题、解决问题也许关系就会柳暗花明、豁然开朗。那么，“指数函数与对数函数”是一种什么关系呢？先让学生计算y=2x和y=log2x的函数y值，并引导学生进入思考，诱导学生在情境的氛围中进行探索和研究。

（二）抛出问题，诱导启发

通过提出问题引导学生自主探究，可以改变“老师滔滔讲、学生默默听”的现状，变被动为主动，让学生在教师的指导下，培养独立研读、独立思考、独立解决问题的能力。学生的自主探究需要教师“画龙点睛”式的指导，以“问题”贯穿“教”的基本思想，将大大促进教学目标的实现。

（1）首先，让学生通过自主学习，计算得到如下结果，让学生仔细观察两个函数对应值表（参见表1、表2），抛出问题1：两组点的坐标有什么关系？

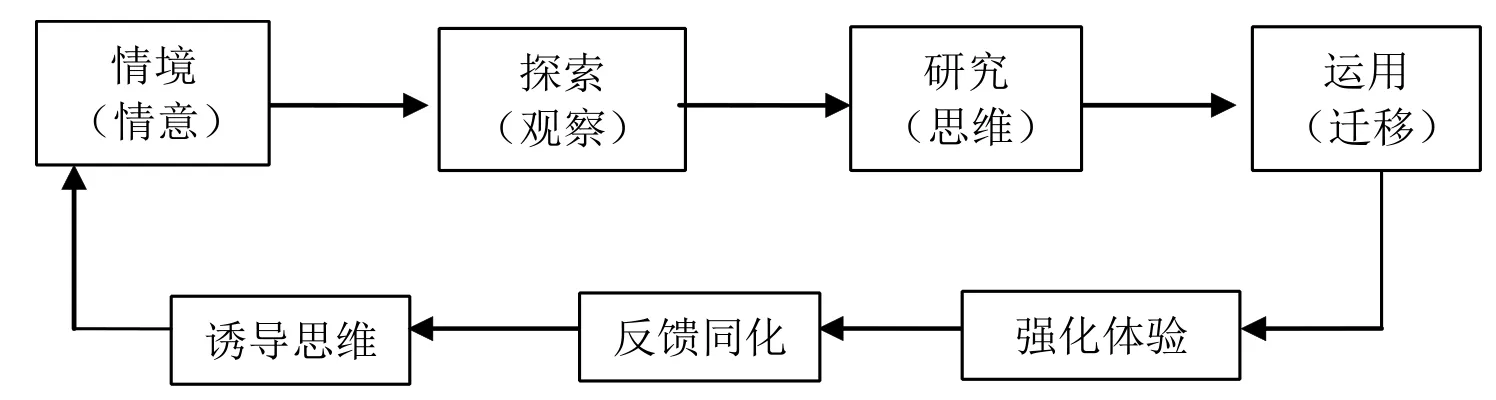
图1 探究学习方式图（简化）

表1

表2

（2）其次，让学生动手，根据x和y值，做函数y=2x与y=log2x在同一坐标系内的图像（参见图2），引导学生探究问题2：两个函数图像之间又有什么关系？通过对比你得到了什么结论？

由此可见，“问题”诱导要符合所教内容本身的内在逻辑，要了解学生的知识储备基础，秉承“循序渐进”的原则进行合理设计，根据教学目标选择有代表性和启发性的问题或习题，才能真正发挥“诱思”的作用，激发和完善学生自主学习的动机。

（三）拓展迁移，探究结论

拓展迁移是学习过程中的关键环节，是指学生对已初步获得的知识和能力进行一般化和更大范围的灵活运用，使学生将已有知识在新情境问题中迁移，进而深化对知识的理解与巩固。针对“指数函数与对数函数的关系”，从函数值的关系和函数图像的关系来进行：

（1）通过对y=2x和y=log2x函数值的观察，主要目的在于拓展到一般形式的指数函数与对数函数值的关系，抛出问题3：指数函数y=ax与对数函数y=logax(a〉0,a≠1)有何内在关系？通过学生之间的讨论，并发表不同看法，进而激发学生的创造性思维，探究得出结论。

（2）通过y=2x和y=log2x函数图像关系的自主学习，主要在于延伸到一般形式的指数函数与对数函数图像的关系，抛出问题4：同底的指数函数与对数函数的图像之间有什么关系?进而将指数函数与对数函数的关系进行抽象提升，形成反函数的概念，并尝试让学生总结反函数的定义。

拓展迁移要求教师引导学生从具体到抽象，对知识进行归纳整理,获得结论,进而逐渐发现并认识反函数的概念、特性及原理，不断在旧知识基础上建构新的知识结构，形成相对完整的知识结构体系。在此过程中，得到学习成功的情感体验，也获得了学会学习的技能，对学生整体素质的提高大有益处。

图2

（四）练习运用，检查反馈

及时强化和运用已获得的教学效果是非常重要的。以练习或测验的方式发现存在的问题，运用课堂练习不断强化之前探究的基本结论，“变学为思、变学为悟”[4]，使教学结果不断得到反馈。在此过程中，学生也可以不断进行自我检查和调整，对学习效果有一个自我评价，从而调整学习方法，学习效果也会得到提高。在“指数函数与对数函数的关系”课堂中，也要不断进行强化和反馈。如，求y=3x+1的反函数，检查学生求反函数的步骤；又如，已知函数y=f(x)图像过点（-2，1），则y=f-1(x)图像必过哪个点？

总之，“诱思探究学习”契合了当前教育教学发展的主流思想和本质，变填鸭式、满堂灌的教育教学模式为启发式教学，充分体现了“教师主导、学生主体”的双边关系；变单一的知识传授为知识、情感、能力等综合素质培养，充分体现了“学生全面发展”的意识，如果可以在学科教育教学中主动运用这一模式，能够达到充分提高课堂教学效果的目的。本文以“指数函数与对数函数的关系”为例进行的课堂教学设计，也仅是运用这一教学模式的初步尝试，笔者也将随着教育教学实践的不断深入，不断进行修正和完善，使学科教学实现“全面育人”的目的。▲

[1]裴娣娜.教学论[M].北京：教育科学出版社，2007：129.

[2]张熊飞.诱思探究学科教学论的研究和实践[J].教育研究，2002（9）：50-60.

[3]张熊飞.“诱思探究学科教学论”研究50年[J].课程·教材·教法，2014（2）：4-13.

[4]吴永熙，张德启.从《学记》及“诱思探究”教学理论谈可持续发展教育[J].教育发展研究，2001（9）：74-77.