斜拉－自锚式悬索协作体系桥梁成桥状态分析

巴卫强，苗战涛，曹恒涛

(河南省交通科学技术研究院有限公司，河南 郑州 450006)

0 引言

悬索桥和斜拉桥是大跨度桥型的首选形式。大多数悬索桥以地锚式为主，这需要巨大且昂贵的锚锭抵抗主缆的强大拉力。自锚式悬索桥主缆锚固在加劲梁上避免建造锚碇，而且还可为加劲梁提供附带的预应力。斜拉桥、悬索桥单一桥型表现出了各自的缺点和不足，已不能满足实际工程要求。因此斜拉－自锚式悬索协作体系桥应运而生。它既体现了两者的优点，又弥补了两者的不足。缆索体系桥的设计过程中，塔梁截面形式及尺寸确定后，由于荷载是由梁、塔和索共同分担的，合理地确定它们分担的比例至关重要。因此此类桥的设计首先是确定合理的成桥状态，即合理的线形和内力状态。而斜拉－悬索协作体系桥是一种新桥型，其成桥状态研究较少。本文通过分段悬链线理论计算无应力索长，在通过影响矩阵法和几何非线性理论进行迭代，进而确定成桥状态。利用该法对某斜拉－悬索协作体系桥进行了计算，得到的线形和索力符合实际要求。

1 成桥设计状态的确定

悬索桥的主缆在施工过程中几何非线性突出，自锚式悬索桥还存在主塔与加劲梁的梁柱效应，它们对结构内力和整体变形影响很大。悬索桥初始平衡状态分析的重点为缆索系统的计算分析。

1.1 自锚式悬索桥段成桥状态确定

当前，悬索桥成桥主缆线形的确定方法主要有抛物线法、以悬链线索元为基础的递推法、虚拟梁法等。抛物线法计算简单，但精度不高，适用于悬索桥的初步设计;悬链线法精度高。根据背索斜拉索所分担的加劲梁梁段的自重及二期恒载计算出背索索力，由副塔背索作用点形心点处的力矩平衡可得出主缆对副塔的水平力H 及竖向力V。设全桥沿水平均布的结构自重和活载的总和为q，则边跨主缆的水平分力H 为:

由上式可计算得出矢跨比λ。

考虑到具体情况，主缆成桥时所承担荷载为沿主缆弧长均布的主缆自重及吊索传递的集中力，因此悬索桥的主缆受力图式可简化为承受沿弧长均布荷载设有集中力的柔性索，各吊点之间的主缆线形为受主缆自重作用的悬链线，即整个主缆可以视为按吊点划分的多段悬链线的组合，如图1所示。

对于任意第i 段悬索，其方程为:

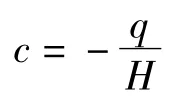
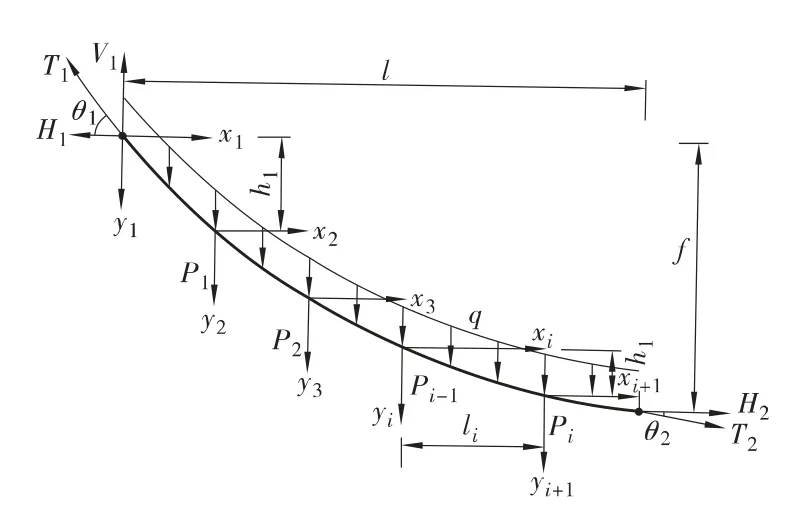
图1 主缆受力分析

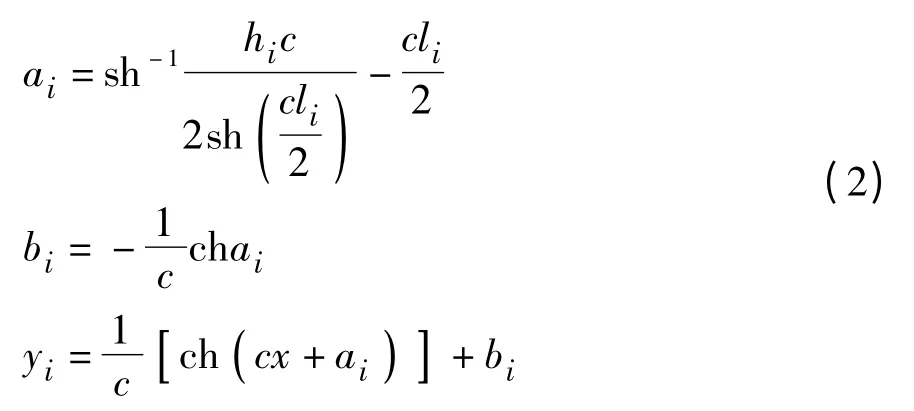
对于主缆整体有如下平衡方程:

式中:si为第i 段的索长，可表达为

而各段之间在集中荷载作用点处满足如下受力平衡条件:

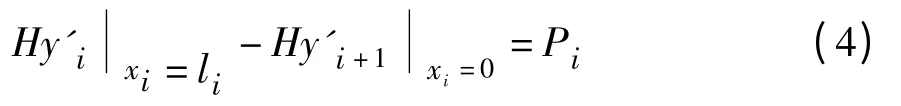
其中Pi为集中力，包括索夹和吊索自重以及由吊索所承担的加劲梁、桥面系等荷载，l、H 为主缆两端的水平距离和高差。计算时需要先给一定的初始值，进行迭代得到精确的线形。

1.2 斜拉桥成桥状态确定的方法

密索体系使斜拉桥成为高次超静定结构，且在施工中结构体系在不断转换，如何确定在施工过程中斜拉索的初张力和体系完成之后的调索力，以达到合理的成桥受力状态，国内外学者提出了很多理论及计算方法，主要包括:刚性支承连续梁法、零位移法、内力平衡法、最小弯曲能量法、最小弯矩法、最小用索量法和影响矩阵法等方法进行调索。但上述索力优化方法都有各自的局限性，本文采用一种综合方法。

1.2.1 用最小弯曲能量法确定成桥状态

首先将斜拉索、主梁、主塔的轴向刚度增至足够大，进行一次成桥计算，这样能得到一个在主梁和塔内弯矩均比较小、目标索力也基本均匀的成桥状态。这种成桥状态下，少数索的索力可能不太合理。但该成桥状态并不是最终目标，而是进行成桥状态调整的基础。

1.2.2 影响矩阵法索力调整

通过索力调整，使初步确定的成桥状态的主梁和塔中弯矩以及索力合理化。

式中:［A］为索力调整对控制目标的影响矩阵;{ ΔT }为待求的成桥索力调整量;{ ΔR }为成桥状态控制目标需调整的量。

以每根索的张拉延伸量作为变量，以成桥状态的所有索力以及主梁和塔中所有控制截面的弯矩作为目标，在上一步的基础上进行一次全桥的索力调整。其中索力目标和控制截面弯矩目标应根据设计要求进行设定，索力的调整可根据加劲梁弯矩均匀性，同时考虑使主塔变位和弯矩，控制截面弯矩可综合考虑截面抗弯能力以及活载内力来进行索力调整。采用最小二乘法求解，解出 { ΔT }后，即得到调整后的控制目标值:

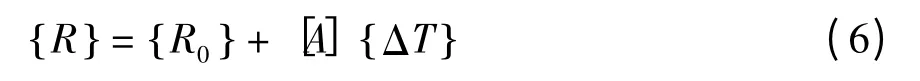
式中:{ R }为调整后的控制目标值;{ R0}为控制目标在调整前的值;［A］、{ ΔT }同上。在采用最小二乘法求解时可引入加权系数，通过调整加权系数来改变调整后的成桥状态。

2 精确平衡状态分析

对于自锚式悬索桥，由于其主缆和主梁是连接在一起，主梁将受到很大的轴力，加劲梁的两端和主塔顶部会产生相应的位移，即主缆体系将发生变化，严格意义来说上述初始平衡状态分析计算得到的主缆线形和无应力索长与实际并不相符，所以必须对整体结构重新进行精确分析，这样的问题可通过杆系单元输入初始内力来解决。到结构的初始平衡状态后，把计算的主缆和吊杆的反力作为外力施加在杆系单元上，计算加劲梁和索塔墩的初始内力，并将其作用在整体结构上，通过反复计算直至收敛，以获得精确整体结构的初始平衡状态。

获得所有缆索单元的无应力长度、梁和塔的初始内力后，并把这些结果应用于整体模型对模型进行几何非线性分析计算，进行局部调整，最终得到自锚式悬索协作体系桥的成桥状态。

3 工程算例

某斜拉－悬索桥主桥长555 m，为三塔斜拉－自锚式悬索组合体系桥，包括主塔斜拉索体系段与自锚式悬索体系段。主桥跨径组合为:25 m+90 m+2 ×162.5 m+90 m+25 m=555 m。

斜拉索体系段为双索面斜拉桥结构体系，自锚式悬索体系段为自锚式悬索斜拉背索组合结构体系，副塔靠近河堤侧设置自锚式悬索，悬索为空间三维线形。

本文采用有限元专用程序MIDAS/Civil 来对三塔斜拉－自锚式悬索协作体系桥进行三维建模，结构由加劲梁、主塔、副塔、主缆、斜吊索、吊杆组成。

主梁的模拟:采用“单梁式”(即鱼刺骨模型)即主梁的刚度(竖向、横向挠曲刚度和扭转刚度)、质量精确模拟主梁的刚度和质量，将质量都集中在中间节点上，中间节点和吊杆采用刚臂或主从关系横向连接。全桥模型如图2。

图2 全桥计算模型示意

3.1 成桥线性分析结果

该桥副塔左右结构不对称，在恒载作用下，主缆拉力和背索拉力对副塔根部将产生不平衡弯矩，为保证副塔安全故需控制此弯矩在一定范围内。据此原则，确定主缆拉力及吊杆承担的加劲梁重量比例。进行非线性有限元平衡迭代计算，确定合理成桥状态。成桥状态计算得到副塔最大弯矩为－419 635 kN·m，最大轴力为－115 519 kN(均为塔根处)，加劲梁最大弯矩为－159 137 kN·m，最大轴力为－323 872 kN。自锚式悬索段主缆线形如图3、表1。成桥状态下加劲梁的内力图如图4所示，副塔内力图如图5所示。

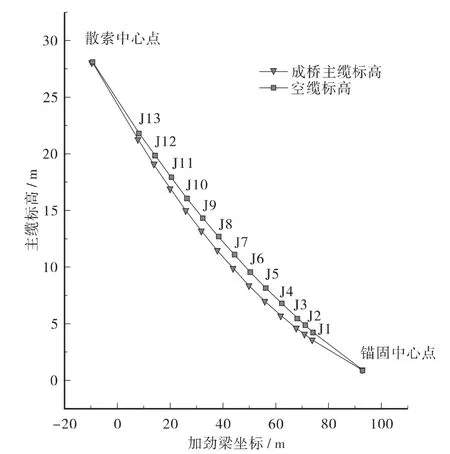
图3 主缆成桥和空缆线形

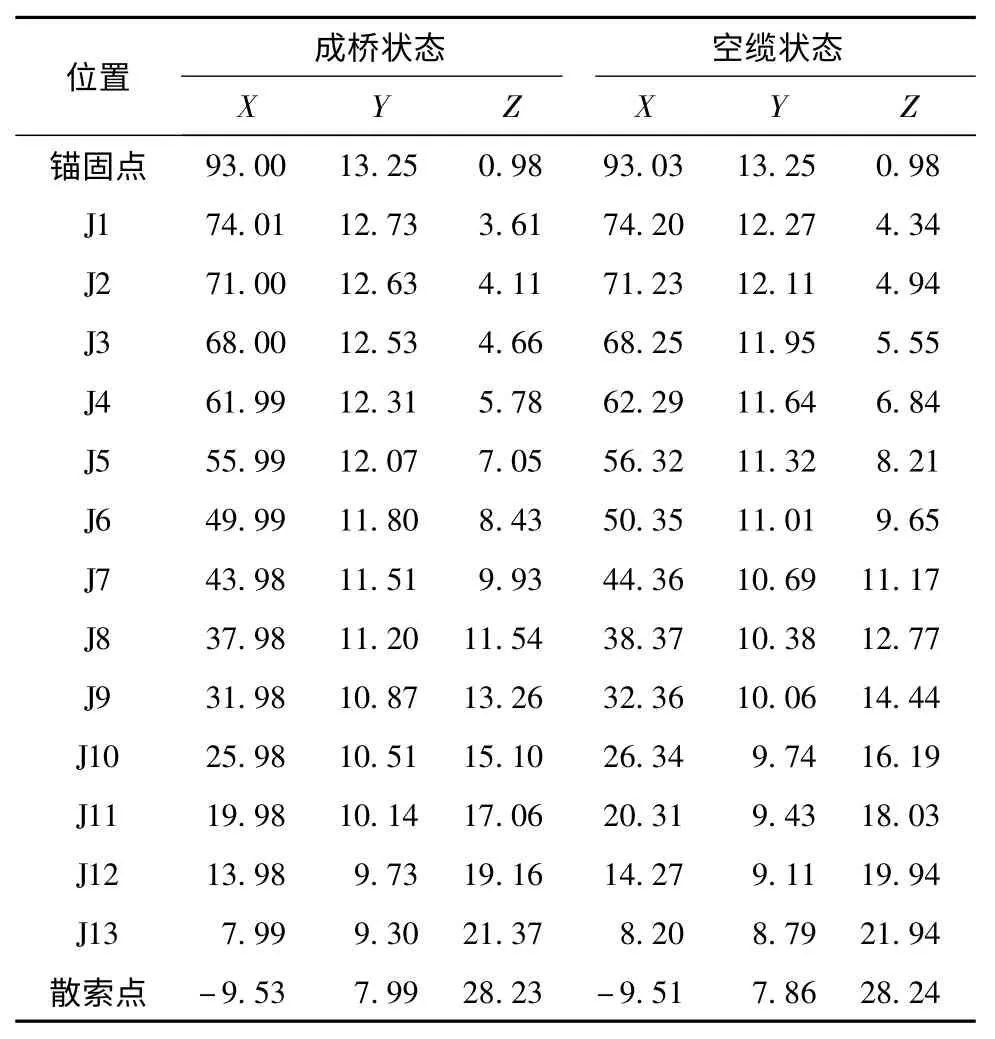
表1 主缆成桥和空缆坐标 m

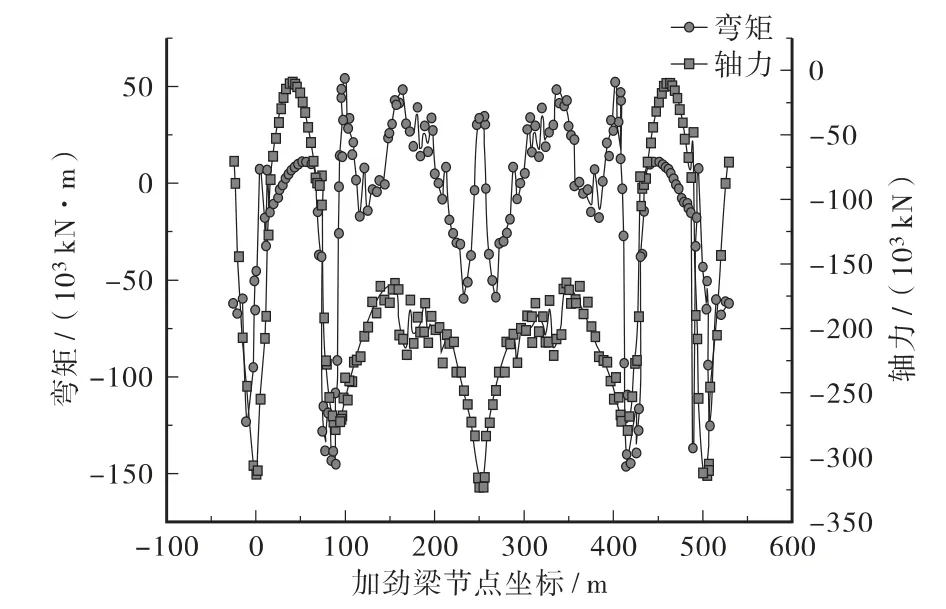
图4 成桥状态加劲梁轴力和弯矩图

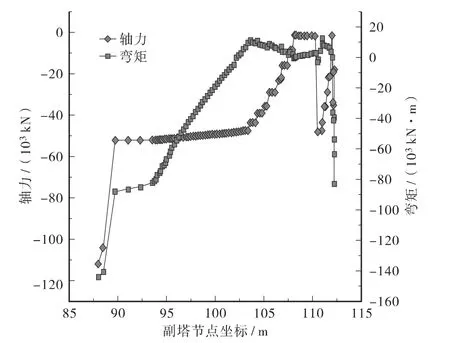
图5 成桥状态副塔轴力和弯矩图

3.2 成桥斜吊杆、背索及拉索内力分析结果

斜吊杆内力见图6、表2，斜拉部分斜拉索内力见图7。

成桥状态下背索索力见表3所示。

图6 斜吊杆内力

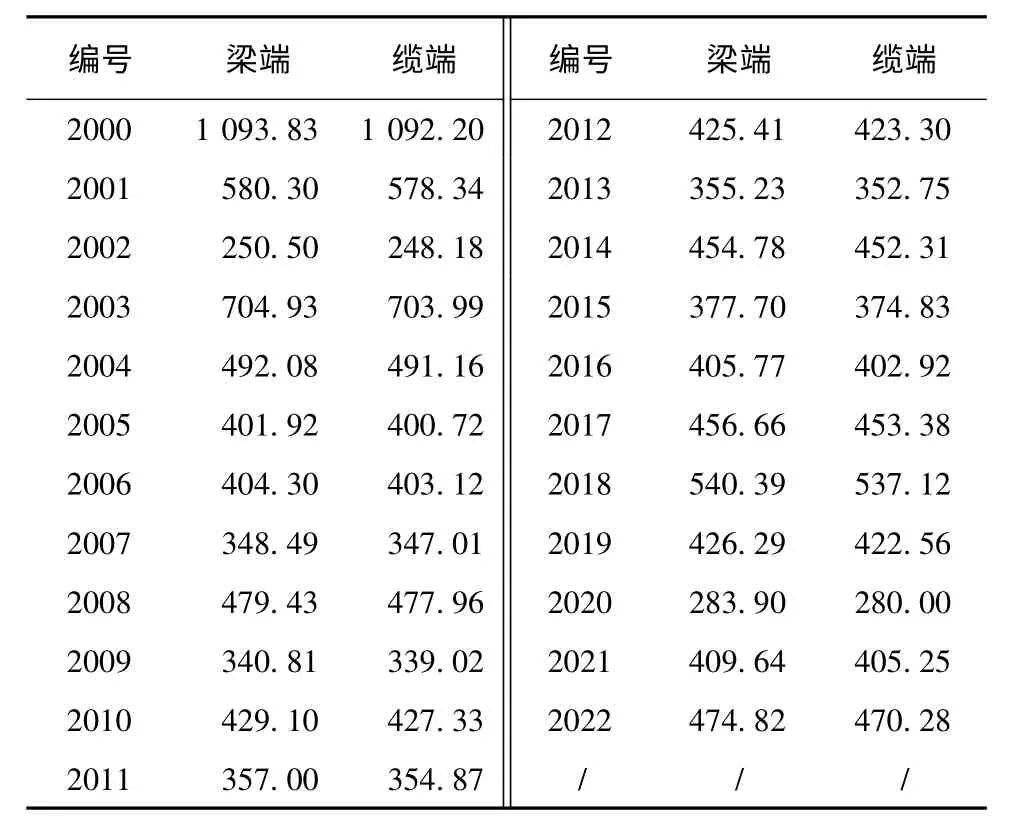
表2 斜吊杆内力 kN

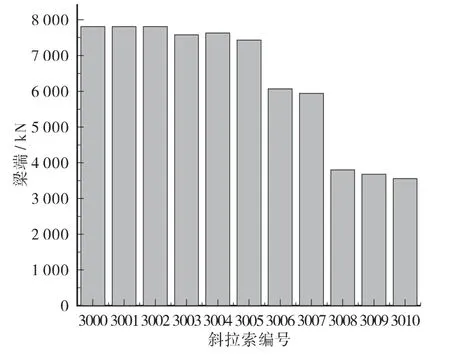
图7 斜拉部分斜拉索内力

从上表可见，成桥状态下背索索力基本在6 200～6 600 kN 之间，索力比较均匀。

成桥状态下斜拉索索力见表4所示。

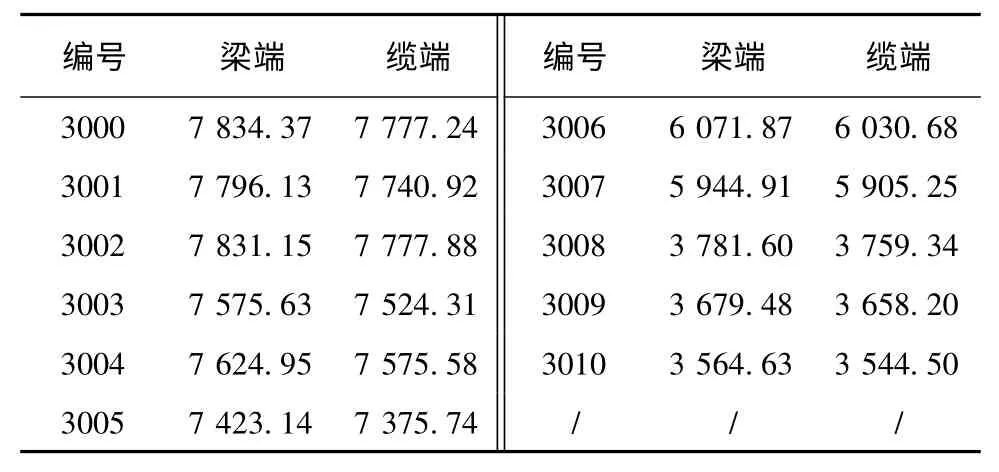
表4 斜拉索内力 kN

从上表可得，成桥状态下索力分为两部分，单元编号 3000～3007 的索力在 6 000～7 800 kN 之间，单元编号3008～3010 的斜拉索索力在3 500～3 800 kN 之间，索力符合大跨斜拉桥的设计要求。

4 结论

1)本文对采用空间主缆、吊索及斜拉索体系的三塔斜拉－自锚式悬索连续协作体系桥进行受力分析。首先利用分段悬链线法迭代计算其合理线形，再利用有限位移理论计算吊杆和加劲梁内力，进而迭代出空缆状态线形，主缆无应力索长，最终得到合理成桥状态。

2)提出了对于副塔两侧不对称时成桥线形及内力的迭代计算方法，通过该方法能迅速找到全桥的合理的平衡状态。

3)结合工程实例，利用上述方法进行分析计算，加劲梁最大弯矩为－159 137 kN·m，最大轴力为－323 872 kN，主缆水平分力最大为20 571 kN，吊杆索力均匀。实例验证该方法可行，可用于同类桥梁成桥状态的计算。

［1］蔡迎春，万 超，郑元勋.中国自锚式悬索桥发展综述［J］.中外公路，2013(4):143 －147.

［2］陈明宪.对我国公路桥梁建设创新的思考［J］.长沙理工大学学报(自然科学版)，2006(3):113 －117.

［3］李传习，柯红军，刘海波，等.空间主缆自锚式悬索桥成桥状态的确定方法［J］.工程力学，2010，27(5):137 －146.

［4］张 哲.混凝土自锚式悬索桥［M］.北京:人民交通出版社，2005.

［5］胡建华.现代自锚式悬索桥理论与应用［M］.北京:人民教育出版社，2008.

［6］刘士林，梁志涛.斜拉桥［M］.北京:人民交通出版社，2002.

［7］杨美良，何恒波，谭海亮，等.斜度对多梁式连续斜交小箱梁桥力学性能的影响［J］.长沙理工大学学报(自然科学版)，2014(1):30 －36.

［8］李 熠，颜东煌，李学文.混凝土斜拉桥合理成桥状态研究［J］.重庆交通大学学报，2008，27(6):1017 －1023.

［9］陈建英.响应面有限元法在既有混凝土桥梁可靠度分析中的应用［D］.长沙:长沙理工大学，2005.

［10］刘厚军，刘 钊.自锚式悬索桥吊索张力及主缆线形的设计研究［J］.土木工程学报，2008(3):79 －83.

［11］吴关良.高墩大跨连续刚构桥设计计算分析及合龙方案优化研究［D］.长沙:长沙理工大学，2007.

［12］李东斌.桥梁结构拓扑优化方法及其应用研究［D］.长沙:长沙理工大学，2007.

［13］阳 斌.桥梁结构的精细计算及软件开发研究［D］.长沙:长沙理工大学，2013.