中央扣对大跨悬索桥行车激励响应的影响

吴海军

(湖南省交通科学研究院，湖南 长沙 410015)

0 引言

悬索桥是为减小悬索桥跨中挠度和加劲梁伸缩量，可以采用中央扣的方法，即在主跨跨中处将主缆和加劲梁直接固结，相当于增加了一个半刚性支承点［1］。悬索桥在车列荷载作用下，加劲梁和主缆将产生纵向位移，且缆、梁位移不同步，极易引起吊索弯折，而加设中央扣能有效地改善跨中附近短吊索的受力性能和抗弯折能力［2］，同时可以限制主缆与加劲梁之间的纵向水平位移，从而提高悬索桥的纵向刚度［3］。悬索桥采用设置中央扣的方法可以减小非对称荷载作用下的挠度［4］，提高纵桥向位移复原力，降低正常情况下活载引起的振动以及风和地震作用引起的纵桥向位移［5］。

中央扣是改善悬索桥受力状态的常用构造，自1959年法国的坦卡维尔悬索桥(主跨608 m)首次设置中央扣以来［6］，许多悬索桥均采用了这种方法。中央扣可以采用钢结构三角桁架构成的刚性中央扣，也可以采用斜拉索构成的柔性中央扣，如国内的润扬长江大桥(主跨1 490 m)采用的是刚性中央扣，矮寨特大悬索桥(主跨1 176 m)则采用柔性中央扣［7，8］。

本文以澧水特大桥位为研究背景，基于ANSYS建立了该桥的3 种中央扣模式和未设置中央扣的空间动力模型，分析了单辆55 t 标准重车匀速通过悬索桥时桥梁结构的动力响应，较为深入地讨论了中央扣形式的不同及车辆移动速度的不同对悬索桥结构动力响应的影响，为悬索桥的设计提供了参考。

1 背景工程

澧水特大桥为张家界至花垣高速公路上的一座特大型桥梁，桥位区地处张家界永定区与湘西自治州永顺县的交界处，属构造侵蚀低山丘陵地貌，桥位横跨澧水河峡谷［5］。

澧水特大桥主桥采用单跨简支钢桁架悬索桥，主缆跨径布置为(200+856+190)m，主缆矢跨比为1/10，2 根主缆横向间距为28 m，在花垣岸边跨为适应路线线形的变化，避免锚碇与路线冲突，主缆中心间距由28 m 变化到 38 m，在平面上呈八字形［6］。全桥采用69 对吊索，吊索标准间距为12.0 m，端吊索至索塔的距离为20 m。钢桁梁全长为854 m，桁高6.5 m，桁宽28.0 m，节间长度6.0 m，在桥塔下横梁处设竖向支座及横向抗风支座，跨中设柔性。大桥全宽为24.5 m，组成为0.5 m(防撞栏杆)+11 m(行车道)+0.5 m(防撞栏杆)+0.5 m(中央分隔带)+0.5 m(防撞栏杆)+11 m(行车道)+0.5 m(防撞栏杆)。设计荷载为公路－Ⅰ级，设计时速80 km/h。桥面纵坡0.9%，横坡2.0%。如图1。

钢桁加劲梁由主桁架、主横桁架、上下平联及抗风上稳定板组成。主桁架为带竖腹杆的华伦式结构，由上弦杆、下弦杆、竖腹杆和斜腹杆组成。上弦杆、下弦杆采用箱形截面，除支座处腹杆采用箱型断面外其余均采用工字型截面。主桁桁高6.5 m，桁宽28 m，标准节间长度6 m。一个标准节段长度12.0 m，由2 个节间组成，在每节间处设置一道主横桁架。主横桁架采用单层桁架结构，由上、下横梁及竖、直腹杆组成，其中上下横梁采用箱形截面，腹杆均采用工字型截面。上、下平联均采用K 形体系、工字型截面。

图1 澧水特大桥桥型布置图(单位:cm)

2 分析说明

2.1 汽车车辆

背景项目采用公路－Ⅰ级为设计荷载，故本文采用公路－Ⅰ级车辆荷载作为研究荷载，即5 轴共55 t重车，其轴重分布如图2所示。

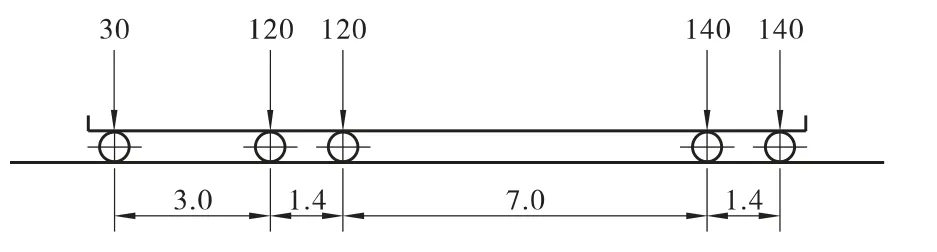
图2 分析中采用的汽车模型(长度单位:m，轴重单位:kN)

2.2 分析工况说明

由于背景工程设计时速为80 km/h，故选取4个正常行驶车速和1 个超速行驶车速作为分析车速，同时为确定汽车作用下桥梁的实际响应情况，进行了汽车考虑冲击系数的静态布载分析，分析工况如表1所示。

表1 分析工况一览表

2.3 分析方法说明

本文采用分析软件为通用有限元软件ANSYS。加劲梁、主塔采用空间梁单元(BEAM189)模拟;主缆及吊索采用空间杆单元(LINK10)模拟，并利用Ernst 公式对其弹性模量进行修正［7］;桥面板采用弹性板单元(SHELL63)模拟。主塔底部及主缆端部边界条件考虑为固结，加劲梁与主塔间边界条件考虑为非线性刚度的支座连接。建立的ANSYS 模型如图3所示，模型共1 776 个节点，4 217 个单元。

由于悬索桥几何非线性效应明显，在计算中必须考虑构件的几何刚度，因此在模型中根据成桥状态的内力状况赋予了各单元的几何刚度初始荷载和初始单元内力，以便形成结构刚度进行后续计算。

在对大跨度悬索桥进行行车动力分析时，由于车辆本身的质量、刚度相对于主桥来说影响很小，故可以忽略不计，从而减小了求解微分方程的难度，同时计算出来的桥梁动力响应也是准确的［7］。故可以把移动车辆处理为移动荷载进行分析，动力平衡微分方程为［8］:

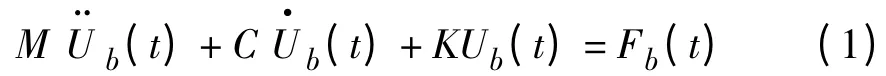
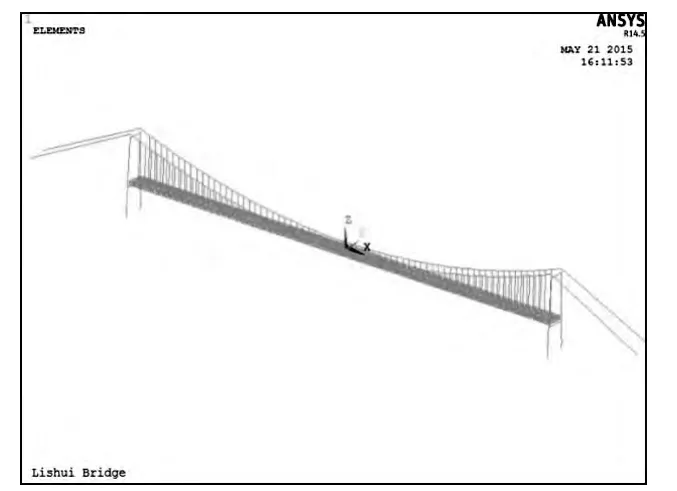
图3 澧水特大悬索桥有限元模型图

其中:Ub(t)为桥梁的自由度向量;M、C、K 分别为桥梁的质量、阻尼和刚度矩阵;Fb(t)为桥梁所受车辆的外力列向量。

在结构的动力响应分析，尤其是长时间的振动响应分析中需要考虑阻尼的作用，本文采用悬索桥结构的阻尼是 Rayleigh 阻尼［9］。Rayleigh 阻尼模型是广泛采用的一种正交阻尼模型，其数学表达式如下:

其中，α、β 为 Rayleigh 阻尼常数。

基于ANSYS 瞬态动力学非线性分析功能，时程分析采用HHT 法。HHT 递推格式以 Newmark 方法为基础，其基本递推公式如下［9］:

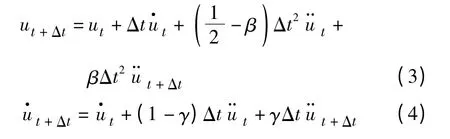
3 分析结果

3.1 位移分析结果

根据计算结果，主梁节点最大竖向位移并不是出现在跨中位置，下面给出其最大竖向位移具体结果，如表2所示。

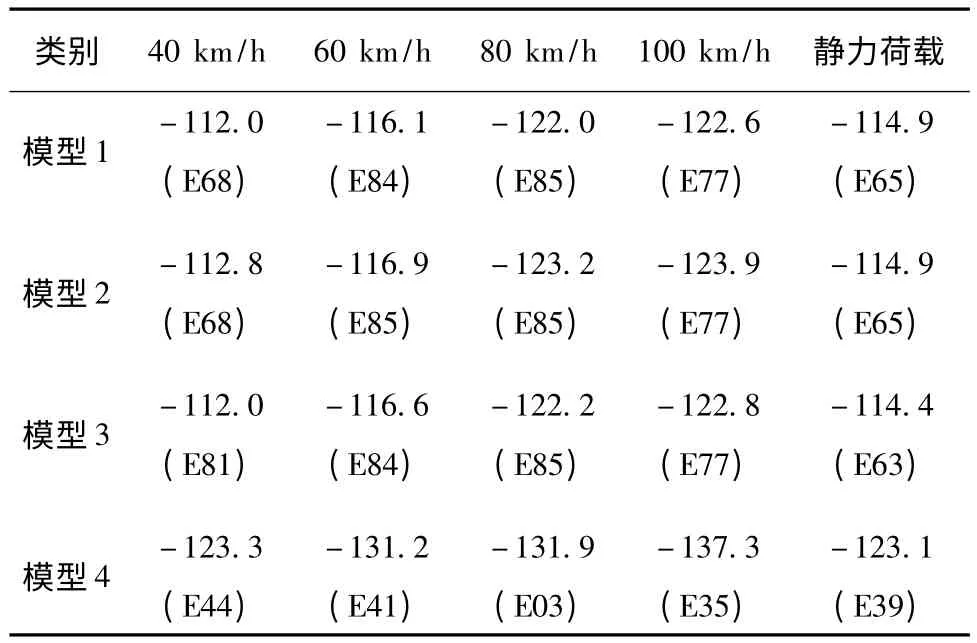
表2 主梁最大竖向位移结果 mm

从表2中可以看出，在不同车速情况下，车速越大同一模型中的位移值也越大，且呈非线性增长;模型1 与模型3 在相同车速下的最大位移值相差较小，模型 2 最大位移值较模型 1、3 大，且模型 1、2、3的值均比模型4 小，说明刚性中央扣与3 对柔性中央扣对桥跨的刚度贡献比1 对柔性中央扣大。在设计车速下，主梁各节点的最大竖向位移如图4所示。

从图4中可知，在设计车速下，无中央扣时竖向位移最大值出现在中跨的1/4 跨附近，设置了中央扣后，1/4 跨附近的竖向位移明显减小，且有无中央扣对跨中的竖向位移最大值影响并不显著。

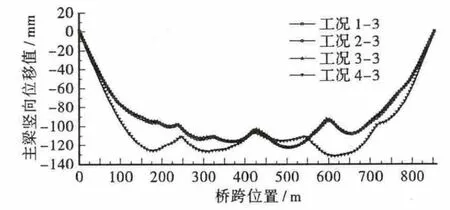
图4 主梁节点最大竖向位移图

3.2 钢桁梁内力分析结果

取跨中附近单侧两个节段作为研究对象，进行中央扣对钢桁梁局部内力响应的分析，钢桁梁、中央扣及主缆、吊索的编号见图5。

图5 主梁跨中区段杆件编号

为综合考虑中央扣对杆件的拉压效应的影响，此处采用轴力幅值的方法对结果进行分析。图6给出了主梁跨中区段主要杆件的轴力幅值，由于跨中区段杆件内力极值基本是关于跨中截面对称的，故此处仅给出了一半的内力幅值。

由图6可知，在不同车速情况下，车速越大同一模型中的杆件轴力幅值也越大，且不同杆件的内力幅值有大有小，说明不同构件对车速的敏感性不同;模型3 的轴力幅值较其他3 个模型的要小，这是因为模型3 的中央扣有3 对斜吊索，其余的斜吊索能很好地分担跨中斜吊索的轴力。

模型1、2、3 的斜吊索轴力时程图如图7所示，限于篇幅，此处仅给出了设计时速下斜吊索的轴力时程曲线。

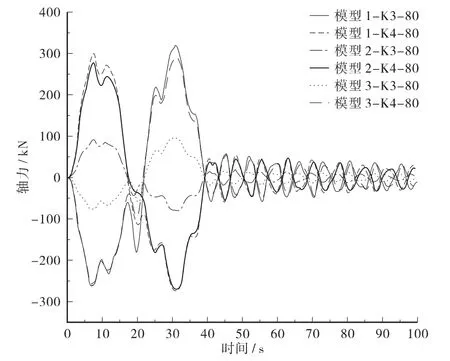
图7 设计时速下斜吊索轴力时程图

由图7可以看出，模型1 与模型2 的相同斜吊索轴力时程曲线较接近，且模型2 的峰值较模型1的低;对于模型2，在整个加载历程中始终有1 根一直处于受拉状态，由此可见，采用1 对柔性中央扣时，其一侧柔性斜吊索已退出工作，降低了中央扣作用，因此宜采用刚性中央扣或3 对柔性中央扣。

3.3 钢桁梁冲击系数

根据计算模型推算出全桥钢桁梁的冲击系数曲线如图8所示，钢桁梁最大冲击系数见表3。

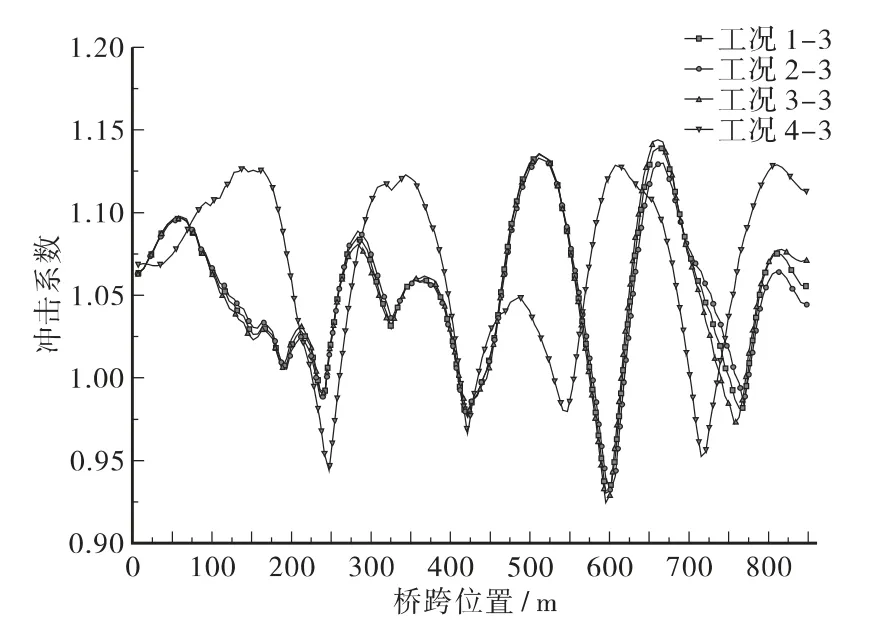
图8 设计时速下钢桁梁冲击系数

从图8给出的全桥钢桁梁冲击系数变化规律可以看出，车辆激励对不同钢桁梁位置所产生的冲击效应不同，其最大值均超过了规范值1.05;模型4冲击系数波动更大，说明中央扣对降低钢桁梁的冲击系数有着积极的作用;图中模型1、2、3 的曲线不关于跨中对称，这说明了中央扣显著改变了左右半跨的动力响应。

从表3给出的数据可以看出，车速越高同一模型的冲击系数也就越大，在有中央扣的模型中，模型2 相同车速下的冲击系数越大，表明1 对柔性斜吊索的效应较1 对刚性和3 对柔性斜吊索的要小，同时，模型4 在相同车速下的冲击系数越大。

表3 钢桁梁最大冲击系数

4 结论

通过以上的分析比较，可以得出如下结论:

1)对于钢桁梁悬索桥，中央扣的设置能显著减小1/4 跨附近的竖向位移，且在不同车速情况下，车速越大相同模型中的位移值也越大，并呈非线性增长。

2)中央扣宜设置为刚性中央扣或3 对柔性中央扣，设置1 对柔性中央扣时实际运营中会出现一侧柔性斜吊索退出工作的现象，降低了中央扣作用，是不可取的。

3)钢桁梁位置的不同，车辆激励所产生的冲击效应也不同，且其最大值均超过了1.05，中央扣对降低钢桁梁的冲击系数有着积极的作用，且改变了左右半跨的动力响应。

4)车速越高，对钢桁梁的冲击系数也就越大。

［1］严国敏.现代悬索桥［M］.北京:人民交通出版社，2004.

［2］雷俊卿.悬索桥设计［M］.北京:人民交通出版社，2002.

［3］丰 硕，项贻强，谢 旭.超大跨度悬索桥的动力特性及地震反应分析［J］.公路交通科技，2005(8):31 －35.

［4］聂利英，叶爱君，胡世德.大跨度悬索桥地震动力分析中高阶振动的影响［J］.同济大学学报，2001，29(1):84 －88.

［5］苏维映.大跨度悬索桥自振特性及列车过桥响应的研究［D］.成都:西南交通大学，2010.

［6］宋 晖，林 恰，唐茂林，等.中央扣对不同悬吊结构体系悬索桥的影响分析［J］.中国工程科学，2010，12(7):22 －27.

［7］李 瑜.澧水特大桥总体构思及方案比选［J］.公路工程，2011(5):100 －107.

［8］程丽娟.澧水大跨度悬索桥结构设计及受力分析［J］.公路工程，2011(2):111 －114.

［9］王新敏.ANSYS 结构动力分析与应用［M］.北京:人民交通出版社，2014.

［10］蒋 望.钢桁加劲梁悬索桥施工与成桥阶段仿真计算分析［D］.长沙:长沙理工大学，2008.

［11］刘 斌.三塔悬索桥振动特性的研究［D］.成都:西南交通大学，2009.

［12］万 超.中央扣对大跨径自锚式悬索桥动力特性的影响［J］.公路工程，2014(4):103 －106.

［13］许红胜，颜东煌，等.不中断交通进行斜拉索更换施工中车速的影响性分析［J］.中外公路，2014(1).

［14］李永乐.大跨度公轨两用悬索桥风－车－桥耦合振动及抗风行车准则研究［J］.工程力学，2012(12):114 －119.

［15］徐 勋.大跨悬索桥动力特性的敏感性分析［J］.东北林业大学学报，2009(2):44 －45.

［16］JTG/T D60 －01 －2004，公路桥梁抗风设计规范［S］.