感应耦合与谐振耦合无线电能传输的 比较研究
刘红伟 张 波 黄润鸿 肖文勋 郭上华
(1.珠海许继电气有限公司,广东 珠海 519060;2.华南理工大学电力学院,广州 510640)
早在大规模有线电能传输之前,无线电能传输在一百多年前就由伟大的发明家Nikola Tesla 提出,并且申请了专利[1]。但此后并没有突破性进展,一直停留在可分离变压器模型[2]。直到20 世纪90年代,新西兰奥克兰大学的学者提出了ICPT 技术的概念[3],并且在轨道电车非接触充电方面取得了实质性的进展[4],才引起了国际上的广泛关注。2007年,MIT 的Marin Soljačić 教授及其研究团队运用电磁近场谐振耦合的原理,成功点亮了2m 多外的一个60W 的灯泡,并且传输效率达到40%左右,在1m 的位置甚至达到90%的惊人效率[5],此项技术的突破为中等距离的无线电能传输提供了一个可能的方式[6]。
感应耦合电能传输的基本原理与普通变压器类似,但又有根本的区别。首先,感应耦合是非接触式的,原副边不存在铁心连接。其次,因原副边存在较大的气隙,造成很大的漏磁。并且感应耦合工作在高频的条件下,很多技术问题与传统变压器有根本区别。
谐振耦合无线电能传输有别于以往的感应耦合电能传输,它是利用非辐射电磁近场的储能场的性质,基于光子隧道效应的机理[7],通过共振的方式将高频功率源发出的渐逝波“捕获”,从而实现电能的无线传输。这种强耦合的共振模式不仅仅局限于磁共振,而且存在于光共振、声共振、核磁共振等中[8]。在非辐射近场的范围内,任何发生共振的物体能够实现全方位、高效的能量传输,而很少的能量会向外辐射,并且不受一般外物的阻碍,即能量很少损耗在非谐振物体中[9],显示出此项技术在中等距离无线电能传输诱人的前景。
然而,感应耦合和谐振耦合两种无线电能传输方式在理论模型、电路结构和参数设计上存在诸多相似之处,导致了工程技术人员对二者概念的混淆,已有的文献[10-11]只是从实验上说明两者的区别,并没有从理论上分析,在一定程度上阻碍了无线电能传输技术的发展。本文从两种无线电能传输方式的基本原理和模型出发,阐释了它们的区别和应用场合,为两种无线电能传输系统的设计和应用提供一定的参考和借鉴。此外,在谐振耦合无线电能传输的研究中,物理学家趋向于用耦合模理论来解释,而电气工作者则偏向于电路理论,而本文则统一考虑,研究它们之间内在的联系。
1 感应耦合电能传输
目前对感应耦合电能传输的建模主要有可分离变压器模型和互感模型[12],因感应耦合电能传输是松散耦合的结构,用互感模型来建模比较合适。
1.1 基本原理和模型
感应耦合电能传输系统由分离变压器构成,基本原理是基于电磁感应定律,其基本结构如图1所示,T 型等效电路[13]如图2所示,L1、L2为漏磁参数,M为励磁参数。此种等效电路比较适合于紧密耦合的非接触电能传输系统,作为早期研究非接触式电能传输的模型起到了指导的作用。

图1 感应耦合结构

图2 等效电路图
感应耦合与传统的变压器的不同之处在于:感应耦合电能传输是松散耦合的系统,原边与副边线圈没有直接的铁心连接,存在较大的气隙,在有些系统中,原、副边甚至是没有铁心的空心线圈,因此造成很大的漏磁,磁路的磁动势大部分降在气隙上。解决此问题的办法在于大幅度提高交流功率源的频率。早期的研究工作受变压器强耦合系数的影响,大部分工作注重于如何提高感应耦合电能传输系统的耦合系数,如文献[14]在0.2mm 的范围内效率可以做到92%。近期的研究工作表明在大幅度提高电源频率的同时,在原边和副边线圈引入补偿电容可以大大提高感应耦合电能传输系统的传输功率和效率,并且在理论和实验上证明要实现最大功率传输并不是耦合系数越大越好,而是有一个最优的耦合系数[15]。
感应耦合电能传输突破了传统非接触电能传输系统距离在1cm 以内的限制,达到十几厘米级的传输距离,因此是松散耦合系统,适合用互感模型来描述,主要有 4 种谐振拓扑结构[16],分别为 SS(series-series,串-串),PS(parallel-series,并-串),SP(series-parallel,串-并)和PP(parallel-parallel,并-并)型,其中SS、SP 又称为电压型,PS、PP 又称为电流型[17],其结构如图3所示。

图3 补偿谐振拓扑结构
在此 4 种结构中,都是通过副边谐振频率ωs=1/(LSCS)1/2来决定系统工作频率ω的。文献[12]指出副边补偿电容是为了提高原边向副边传输电能和带负载的能力,原边补偿则是减小无功容量和电源尺寸。并且引入反射阻抗的概念,即副边回路阻抗和互感抗通过互感反映到原边的等效阻抗,可得副边串联补偿的反射阻抗为Zr=(ωsM)2/RW,并联反射阻抗为Zr=ωsM2[RW/(ωsLS)-j]/LS。
据此,以SS 型拓扑结构为例,得到等效电路如图4所示,分析感应耦合电能传输系统的传输功率和效率特性。设原边输入电压为U˙1,电流为I˙1,副边电流为I˙2,其中Zeq=(ωM)2Y11+RS+j(ωLS-1/ωCS)。

图4 SS 型等效电路图
根据等效电路图可得输出到负载的功率

令导数dPo/dM=0,可得系统在最大传输功率目标下的优化互感值
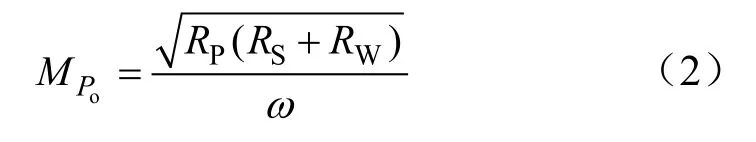
得到的互感优化值对提高系统的功率传输和系统参数的设计具有指导意义。文献[18]给出了不忽略原边线圈电阻RP时4 种谐振拓扑结构在最大功率传输目标下的优化参数。从分析可知,除SS 型外,其他结构的原边谐振频率都不是单个线圈的固有频率。实际此优化参数对固定位置传输电能比较适用,对于向移动设备无线供电,如果要满足此条件将会使控制方法非常复杂甚至无法实现。
分析系统的效率:考虑副边线圈内阻RS,SS型原副边都补偿谐振时,效率为

理论研究表明,SS 型系统当传输功率最大时,效率只有50%[18]。
1.2 关键问题
感应耦合电能传输系统首要解决的是系统的可靠性、安全性和稳定性问题,并且为了实用化,必须提高电能传输功率和效率,降低装置的成本。同时要解决无线传输电能的距离和负载的变化问题以及原副边发生错位和存在障碍物时导致效率明显降低的问题。大量的文献在电压稳定控制[19]、频率稳定控制[20]、负载识别等方面做了卓有成效的研究。文献[21]提出了系统稳定运行的条件,指出要保证系统的稳定高效运行,初级和次级的补偿谐振频率必须相等并且是惟一的,以阻抗相角为零作为谐振的判据。
1.3 应用场合和前景
感应耦合电能传输弥补了传统接触式电能传输的固有缺陷,因此具有很好的应用前景。文献[2]总结了感应耦合电能传输的几种应用,主要应用于不适宜接触连接的危险环境,如潮湿、水下、危险气体和灰尘环境中;植入医疗设备的供电,如人造器官如肾、肝和心脏,听力辅助设备,心脏起搏器等;非接触电池充电以提高可靠性,如电动剃须刀、电动牙刷、以及机器人的非接触供电,新西兰奥克兰大学在电动汽车非接触充电方面作出了卓越的贡献[4],并且与英国一家公司合作,已经进入工程应用的实验阶段;在轨道交通,甚至于磁悬浮列车等大功率非接触供电领域都具有良好的应用前景。
但感应耦合电能传输受传输距离、空间位置和障碍物等的影响而限制了它的应用场合,比较适合于固定负载和距离的情况,特别是在电动汽车充电与智能电网结合方面有很好的前景。
2 谐振耦合无线电能传输
在物理学的定义中,共振是指两个或多个振动频率相同的物体,当一个发生振动时,引起另外物体以最大振幅振动的现象。谐振耦合无线电能传输正是基于这种原理的电能传输方式,在电路上习惯叫谐振。
2.1 近场区的概念
电磁辐射源产生的交变电磁场可分为性质不同的两个部分,其中一部分电磁场能量在辐射源周围空间及辐射源之间周期性地来回流动,不向外发射,称为感应场;另一部分电磁场能量脱离辐射体,以电磁波的形式向外发射,称为辐射场。一般情况下,也分成感应近场、非辐射近场和辐射远场。非辐射近场在λ/2π范围以内,电场强度与磁场强度的大小没有确定的比例关系,相位相差90°,电磁能量在场源和场之间来回振荡,在一个周期内,场源供给场的能量等于从场返回场源的能量,所以没有能量向外辐射,类似于回音壁模式[7],是一个储能场。谐振耦合无线电能传输正是利用近场性质的无线电能传输方式,在中等距离内实现电能的高效传输。
2.2 基本原理和模型
谐振耦合无线电能传输利用电磁近场共振耦合,把能量以“隧道”的形式从一个谐振器高效地传输到另外一个谐振器,而不与或很少与非谐振物体发生能量交换。理论上未被负载吸收部分的能量会返回发射端,从而不会对效率造成影响[22]。耦合模理论(Coupled-Mode Theory,CMT)是适合于分析中等距离近场高品质因数谐振耦合规律的方法,但不适用于非常近距离的耦合和远场的辐射耦合[9]。可以用一组一阶微分方程来描述[5]:
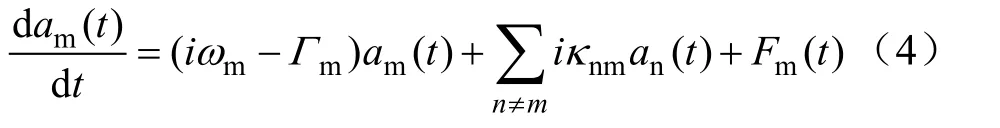
式中,场值am(t)用来表示谐振器m含有的能量|am(t)|2;ωm表示谐振器m的角频率;Γm表示损耗率;κnm表示耦合率,体现能量的传输速率;Fm(t)表示驱动源。Γmam体现了损耗的能量,κnman体现了两个谐振器之间的能量交换。
典型的耦合谐振无线电能传输系统如图5所示。其中,发射线圈S 和接收线圈D 参数完全相同。所谓中等距离指的是无线电能传输的距离至少是装置尺寸的2~3 倍[5]。此系统中,可以通过调节距离改变κS、κ和κd实现阻抗匹配来进行优化。MIT 研究表明,如果能够实现阻抗自动匹配,发射线圈和接收线圈可以分别与驱动源和负载直接连在一起,取消驱动线圈和负载线圈[5]。只考虑发射和接收线圈,此系统可以描述为

式中,ω0为单个线圈的固有频率,且ΓS=ΓD=Γ,可得到场值的表达式为

由d|aD|/dω=0 可知当ω=ω0±(κ2-Γ2)1/2时,场值|aD|有最大值,此时系统发生谐振。由此可见,系统的谐振频率偏离了单个谐振器的固有频率,并且随着耦合率κ的变化而变化。两个频率点对应于MIT的奇模式和偶模式[10],如图6所示。仿真参数为:固有谐振频率f0=10MHz,损耗率Γ=400/s,ΓW=2×104/s,耦合率κ=0.2×106/s。当耦合率κ较小时,不会出现裂频的现象,两个频率点合为一条曲线。

图5 谐振耦合无线电能传输系统
系统的效率的表达式为

相应的效率-频率曲线如图7所示。
由图7可见,当工作频率ω=ω0时,效率最大。把式(6)代入式(7),或根据能量守恒(发射线圈传输到接收线圈的能量等于接收线圈和负载损耗的能量),即
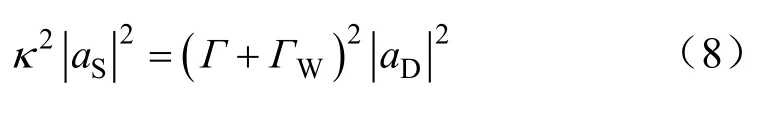
可得


图6 频率分裂

图7 效率-频率曲线
当ΓW/ΓD=[1+κ2/(ΓSΓD)]1/2时,效率最高。可见,最高效率只与强耦合参数κ/Γ有关[10],则
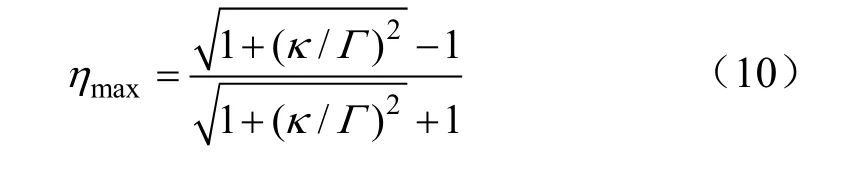
显然,提高效率的关键在于使κ/Γ>>1,即所谓的强耦合条件[5]。κ/Γ是距离和频率的函数,其典型范围为1~50,相应的效率曲线如图8所示。可见,最低效率大于17%,具备一定的实用价值。

图8 最大效率曲线
以磁谐振为例,对于空间螺旋线圈,可以用一个集总参数电感L和电容C来描述线圈的分布参数,则可以确定线圈的自谐振频率(ωS=ωD=ω0)为:ω0=1/(LC)1/2。
线圈的损耗主要是欧姆电阻损耗Ro和辐射损耗Rr,则可得到参数Γ=(Ro+Rr)/(2L)和线圈的品质因数Q=ω0/(2Γ)。
根据耦合模理论,可得耦合率κ=ωM/[2(LSLD)1/2]。利用以上的分析结果,对欧姆电阻损耗和辐射损耗做了平衡优化,确定系统的理想频率范围为1~50MHz[5]。
把Γ=(Ro+Rr)/(2L)和κ=ωM/[2(LSLD)1/2]的参数代入式(9),得到效率的表达式为

式中,R=Ro+Rr,RW为等效到接收线圈的电阻。分析结果与SS 型的结论一致。
再次根据式(7),得到负载功率的表达式
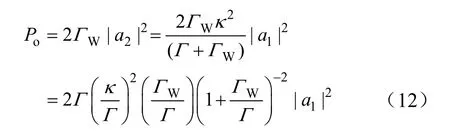
上式对ΓW/Γ求导,可得当ΓW/Γ=1 时,即RW=R,输出功率最大

此时对应的传输效率为

由式(14)可以得出结论,传输功率最大时,随着FOM 的增大,效率最大为50%,结论与SS 型的结论一致。
从上面我们证明了SS 型可以作为研究谐振耦合无线电能传输的模型。文献[23]、[24]分析了多个谐振线圈的模型。以4 个线圈为例,由于发射线圈S 和接收线圈D 之间的距离比较远,因此它们之间的耦合系数kSD是非常小的。假设驱动线圈与发射线圈之间的耦合系数为kPS,接收线圈和负载线圈之间的耦合系数为kDL,根据文献[24],如果参数kPSkDL/kSD=1,那么耦合效率将达到100%(注意不是无线电能传输效率)。因此,虽然kSD由于距离比较远而很小,但可以通过调整kPS和kDL使参数kPSkDL/kSD=1。这就是谐振耦合在线圈距离较远甚至线圈相互垂直时仍然能够实现能量高效传输的原因。
2.3 关键问题
谐振耦合无线电能传输存在以下关键问题:
1)选择适当的谐振频率确定线圈的尺寸。系统频率波长λ、传输距离D和线圈半径r之间存在相互制约关系[25],是设计无线电能传输系统必须考虑的问题。由于目前的空心线圈的高频参数的计算不太准确,导致谐振频率的偏差,只能通过实验来进行调整。用Ansoft 软件进行仿真或通过网络分析仪来得到线圈的参数也是可行的方法。
2)阻抗匹配对系统的传输效率有很大的影响。文献[26]通过阻抗匹配网络来提高系统的传输效率,可以进一步设想:如果能够实现自动阻抗匹配,不仅能够提高效率,而且能够简化系统装置[22]。
3)谐振耦合无线电能传输系统同样存在可靠性的问题,而且系统失谐会导致效率的急剧下降。文献[27-29]提出频率跟踪控制的方法,较好的解决了这个问题。
4)必须解决系统的辐射和电磁干扰问题,并且MHz 级频率是个难控制的公用频段[25]。为了提高效率而增大强耦合参数κ/Γ的代价是提高了系统的辐射水平。文献[8]在量子干涉现象的电磁感应透明原理的启发下,通过引进中继线圈和有规律的旋转发射和接收线圈,使耦合率κ随时间变化,在提高传输效率的同时大大降低了辐射水平。
2.4 应用场合和未来前途
谐振耦合无线电能传输方式不受空间角度、位置,中间障碍物的影响,可以同时给多个负载供电,并且可以设计中继线圈以提高传输距离和效率。因谐振耦合的频率是亚波长,在空间中产生的主要是磁场,对人体基本上没有反应,适合在家居中可构成小型的无线充电网络,随时可以为移动设备,如手机、笔记本电脑、MP3 播放器等充电。在自动化工厂中可以为机器人提供电源,甚至可以为纳米机器人供电。而且应用于植入式医疗设备也优于感应耦合方式。甚至人们设想在公路两旁装设共振天线,向过往的汽车供电[30]。随着技术的不断进步,谐振耦合无线电能传输的应用将会给人们的生活带来巨大的变革。
3 两种无线电能传输方式比较总结
以下对两种无线电能传输方式进行总结:
1)原理不同。感应耦合基于电磁感应定律,采用互感模型,系统工作是因为电流的变化产生磁场耦合的结果。而谐振耦合是基于电场或磁场的共振原理,从物理的耦合模理论出发,推导了高效电能传输的条件,而把电气参数当作中间变量。文献[27,31-32]认为谐振耦合是感应耦合的特例,也就是说谐振耦合是感应耦合当系统线圈处于谐振状态时的情况,并建立了互感电路模型,得到与SS 型感应耦合相同的实验规律。
2)谐振耦合必须满足发射线圈和接收线圈都处于自谐振的状态,而感应耦合只是从减小系统无功容量的目的出发,推导出了优化的补偿电容取值,此时的谐振频率并不是单个线圈的固有频率,而谐振耦合的工作频率是线圈的固有频率。在SS 型中推导出了与谐振耦合相同的条件,与MIT 推荐的电路模型一致,但是此时的SS 型电路是谐振耦合,偏离谐振频率则为感应耦合。这是感应耦合与谐振耦合的重要的区别。
3)传输距离的差异。感应耦合发生在比较近的距离,1cm 内实现高达几百kW 的电能传输,几十厘米也已经能够实现,但发射和接收线圈处于同轴并且之间不能有障碍物;而谐振耦合发生在非辐射近场范围内,不受空间位置和角度以及障碍物的影响,突破了感应耦合电能传输距离的限制,但是传输的功率相对较小。
由以上分析可知,正因为存在以上的不同,导致感应耦合和谐振耦合应用场合的差异。理解两种无线电能传输的区别对无线电能传输装置的设计提供很好的参考价值,对于不同场合采用哪种无线电能传输方案提供一些建议。
4 结论
感应耦合和谐振耦合是极具实用性和发展前景的无线电能传输方式。本文分析了两种无线电能传输方式的基本原理和模型,并推导了相应的数学关系,指出它们在设计时存在的关键问题和之间存在的差异。感应耦合更适合在非常近距离实现能量的高效非接触传输,而谐振耦合因不受空间角度和障碍物的影响,适合于在中等距离范围内的谐振装置之间的能量传输。分析的结果为两种无线电能传输系统的设计提供了一定的指导意义。
[1] Tesla N.Apparatus for transmission electrical energy: U.S.Patent,1,119,732[P].1914.
[2] Fernández C,García R,Prieto R,et al.Overview of different alternatives for the contact-less transmission of energy[C]//Proceedings of the 28th Annual Conference of the IEEE Industrial Electronics Society,10,2002: 1318-1323.
[3] Green A W,Boys J T.10kHz inductively coupled power transfer-concept and control[C]//Proceedings of the 5th International Conference on Power Electronics and Variable-Speed Drives,10,1994: 694-699.
[4] Elliott G J,Boys J T,Green A W.Magnetically coupled systems for power transfer to electric vehicles[C]//Pro- ceedings of the International Conference on Power Electronics and Drive Systems,2,1995: 797-801.
[5] Kurs A,Karalis A,Moffatt R,et al.Wireless power transfer via strongly coupled magnetic resonances[J].Science (New York,N.Y.),2007,317(5834): 83-86.
[6] Soljačić M.Wireless energy transfer can potentially recharge laptops,cell phones without cords[M].San Francisco: Massachusetts Institute of Technology,2006.
[7] 周剑英,戴密特,郝寅雷,等.圆碟中回音壁模式的耦合条件[J].光子学报,2009,38(2): 264-267.
[8] Hamam R E,Karalis A,Joannopoulos J.Efficient weakly-radiative wireless energy transfer: An EIT-like approach[J].Annals of Physics,2009,324(8): 1783- 1795.
[9] Karalis A,Joannopoulos J D,Soljacic M.Efficient wireless non-radiative mid-range energy transfer[J].Annals of Physics,2008,323(1): 34-48.
[10] Ho S L,Wang Junhua,Fu Wn,et al.A comparative study between novel witricity and traditional inductive magnetic coupling in wireless charging[J].IEEE Transactions on Magnetics,2011,47(5): 1522-1525.
[11] Wang Junhua,Ho S L,Fu Wn,et al.A comparative study between witricity and traditional inductive coupling in wireless energy transmission[C]//Electromagnetic Field Computation (CEFC),2010 14th Biennial IEEE Conference on,2010: 1-1.
[12] Chwei-Sen W,Stielau O H,Covic G A.Load models and their application in the design of loosely coupled inductive power transfer systems[C]//Proceedings of the International Conference on Power System Technology,12,2000: 1053-1058.
[13] Hirai J,Tae-Woong K,Kawamura A.Wireless transmission of power and information and information for cableless linear motor drive[J].Power Electronics,IEEE Transactions on,2000,15(1): 21-27.
[14] Esser A.Contactless charging and communication system for electric vehicles[C]//Industry Applications Society Annual Meeting,1993.,Conference Record of the 1993 IEEE,10,1993: 1021-1028 vol.2.
[15] Li Hl,Hu Ap,Covic G A,et al.Optimal coupling condition of IPT system for achieving maximum power transfer[J].Electronics Letters,2009,45(1): 76-U25.
[16] 夏晨阳.感应耦合电能传输系统能效特性的分析与优化研究[D].重庆: 重庆大学,2010.
[17] 孙跃,夏晨阳,赵志斌,等.电压型ICPT 系统功率传输特性的分析与优化[J].电工电能新技术,2011,30(2): 9-12,25.
[18] 孙跃,夏晨阳,戴欣,等.感应耦合电能传输系统互感耦合参数的分析与优化[J].中国电机工程学报,2010,30(33): 44-50.
[19] 赵志斌,孙跃,翟渊,等.电压型CPT 系统动态负载恒压输出研究[J].华中科技大学学报(自然科学版),2011,39(9): 66-71.
[20] 孙跃,王智慧,戴欣,等.非接触电能传输系统的频率稳定性研究[J].电工技术学报,2005,20(11): 56-59.
[21] 武瑛,严陆光,徐善纲.新型无接触电能传输系统的稳定性分析[J].中国电机工程学报,2004,24(5): 63-66.
[22] Stewart W.The power to set you free[J].Science,2007,317(5834): 55-56.
[23] Sample A P,Meyer D A,Smith J R.Analysis,experi- mental results,and range adaptation of magnetically coupled resonators for wireless power transfer[J].IEEE Transactions on Industrial Electronics,2011,58(2): 544-554.
[24] Kiani M,Uei-Ming J,Ghovanloo M.Design and optimization of a 3-coil inductive Link for efficient wireless power transmission[J].IEEE Transactions on Biomedical Circuits and Systems,5(6): 579-591.
[25] 野泽哲生.蓬田宏树,林咏.伟大的电能无线传输技术[J].电子设计应用,2007(6): 42-54.
[26] Beh T C,Imura T,Kato M,et al.Basic study of improving efficiency of wireless power transfer via magnetic resonance coupling based on impedance matching[C]//Industrial Electronics (ISIE),2010 IEEE International Symposium on,7,2010: 2011-2016.
[27] 傅文珍,张波,丘东元,等.自谐振线圈耦合式电能无线传输的最大效率分析与设计[J].中国电机工程学报,2009,29(18): 21-26.
[28] 谭林林,黄学良,黄辉,等.基于频率控制的磁耦合共振式无线电力传输系统传输效率优化控制[J].中国科学: 技术科学,2011,41(7): 913-919.
[29] Kim N Y,Kim K Y,Kim C W.Automated frequency tracking system for efficient mid-range magnetic resonance wireless power transfer[J].Microwave Opt Technol Lett,2012,54(6): 1423-1426.
[30] Soljačić M,Rafif E H,Karalis A,et al.Coupled-mode theory for general free-space resonant scattering of waves[J].Physical Review a,2007,75(5): 1-5.
[31] Yu Chunlai,Lu R,Mao Yinhua,et al.Research on the model of Magnetic-Resonance based wireless energy transfer system[C]//2009 IEEE VEHICLE POWER AND PROPULSION CONFERENCE,VOLS 1-3,9,2009: 374-378.
[32] Cheon S,Yong-Hae K,Kang S Y,et al.Circuit-Model- Based analysis of a wireless Energy-Transfer system via coupled magnetic resonances[J].Industrial Electronics,IEEE Transactions on,2011,58(7): 2906-2914.

