一种新型非线性压电阵列式能量收集器的仿真

沈 威，陶孟仑，陈定方，刘红俊，李鹏辉，明廷鑫

(武汉理工大学 物流工程学院，湖北 武汉430063)

近年来，无线传感网络被广泛应用于军事、智能交通、环境监控、医疗卫生等领域，但是网络节点中的传感器寿命受到了其电源寿命的限制，传统的化学电池的寿命有限，电池的更换工作量大，提高了无线网络的维护成本，而利用环境振动能量为无线网络传感器供电成为解决该供电问题的一个有效途径［1-2］。将振动能量转换为电能有以下3 种常见模式：电磁式、压电式和静电式［3］，其中，压电式能量收集器凭借其尺寸小、易加工、机电能量转换率高和易与电路集成等优点，更适合为无线网络传感器供电。

传统的压电能量收集器是单悬臂梁形式的，文献［4 -6］设计了双稳态压电能量收集器，在一定程度上提高了输出功率。文献［7 -8］设计了压电阵列式能量收集器，与单悬臂压电能量收集器相比，输出功率提高了数倍。但是，以上研究并没有从机电能量转换率的角度对压电能量收集器进行分析和改进，且在输出功率上还存在提高空间。

笔者在线性的压电阵列式能量收集器基础上，引入了非线性磁力，建立了非线性压电阵列式能量收集器的机电耦合模型，并将模型无量纲化，通过Matlab 对线性和非线性的能量收集器模型分别施加白噪声激励，对比分析其输出功率、机电能量转化率。

1 非线性压电阵列式能量收集器模型

1.1 基本结构

图1、图2 所示为笔者设计的非线性压电阵列式能量收集器(nonlinear piezoelectric beam array vibration energy harvester，NPBAVEH)，其有3个相同的悬臂梁阵列式排布，悬臂梁根部粘结有压电片和电路部分。悬臂梁基底材料为铜，压电片材料为PZT，PZT 因具有压电常数大和灵敏度高的特点［9］，成为压电能量收集器中应用最为广泛的压电陶瓷。压电片工作模式为d31 模式，d31模式下应力的方向与电场的方向相互垂直。3 个悬臂梁的端部粘结有同一个磁铁块A，与另外一个固定在基座上的磁铁块B产生非线性磁力，B对A的磁力在x轴方向上的分量为FM;磁铁A在x轴方向上的位移为X;A与B在y轴方向的中心距为d。如图3 所示，将3 个压电片串联，其输出电压比并联高。

图1 非线性压电阵列式能量收集器结构示意图1

图2 非线性压电阵列式能量收集器结构示意图2

图3 非线性压电阵列式能量收集器的电路示意图

1.2 机电耦合模型

外部振动激励通过基座传递到悬臂梁根部，由于3 个形状、结构相同的悬臂梁粘结同一个磁铁块，因此，3 个悬臂梁振动形式一致，振动响应相同，只要求出其中一个压电悬臂梁的电压输出，就可以得出3 个压电悬臂梁的总电压输出。在简谐激励下，求出第i个悬臂梁在一阶模态下的机电耦合模型(i=1，2，3)：

式中：X为磁铁A的垂直位移;Vi为第i个压电悬臂梁的输出电压;m、c、k分别为单个悬臂梁的等效质量、机械阻尼系数和等效刚度;m=M/3 +33/140m1，其中M为磁铁A的质量，m1为单个悬臂梁的质量;Cp为压电片的等效电容;R为外部负载;每个悬臂梁所受的磁力在x轴方向上都是相同的，因此Fmi=FM/3;κc、κV均为机电耦合系数。

为了便于仿真，进行无量纲变换，令x=X/l，则式(1)和式(2)的无量纲形式分别为：

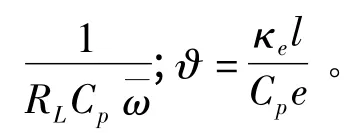
现实中环境振动往往是随机的，因此为了模拟实际情况，在研究NPBAVEH 振动响应时，输入的幅值服从标准正态分布高斯白噪声，即n(t)～N(0，1)，它是压电发电系统研究中最常使用的随机激励。则式(3)可变为：

其中，f为无量纲的激励幅值。

因为3 个压电片串联，所以系统总的输出电压为：

表1 所示为部分物理参数，笔者所取参数值主要参照文献［10 -11］。其中，L为悬臂梁长度;hb、hp分别为悬臂梁和压电片的厚度;le为压电片的长度;l为磁铁A中心到梁根部的水平距离;MA、MB分别为磁铁A、B的磁化强度;VA、VB分别为磁铁A、B的体积。

表1 物理参数表

2 数值计算与仿真分析

2.1 总势能分析

根据式(4)和式(5)，计算NPBAVEH 系统中的a、b、γ、μ、ζ、ϑ 的值分别为1.20、0.30、0.05、0.05、0.01、0.50。

能量收集器系统的总势能包括系统的弹性势能和磁铁在磁场中的势能，可表示为：

a、b取不同值时，系统的总势能图如图4 所示。当a=1.2，b=0.3 时，NPBAVEH 系统势能函数有两个稳定的奇点和一个不稳定的奇点，在两个稳定的奇点附近出现两个势阱。当FM=0时，相当于无磁力耦合作用，即可把能量收集器系统看成线性的压电阵列式能量收集器(piezoelectric beam array vibration energy harvester，PBAVEH)，此时a= -1.5，b=0，势能函数有一个稳定的奇点，且只有一个势阱。

图4 总势能图

2.2 输出功率的对比分析

算得输入激励-fn(t)的方差为σ2，通过Matlab 对式(4)和式(5)进行仿真，得到随σ2变化的输出功率图，如图5 所示。当σ2从小至大取不同值时，对NPBAVEH(a= 1. 2、b= 0. 3)和PBAVEH(a=1.5、b=0)输出电流的平均功率进行对比，当σ2＜1.1 时，NPBAVEH 和PBAVEH 输出的功率相差较为近似，而当σ2＞1. 1 时，NPBAVEH 的输出功率明显大于PBAVEH。

图5 随σ2 变化的输出功率图

2.3 机电能量转换率的对比分析

能量收集器的机电能量转换率可以表示为：

式中：无量纲参数pe、pm分别为输出电流的平均功率、输入机械能的平均功率分别为其相应的瞬时功率。根据式(4)～式(6)的计算式为：

通过Matlab 仿真得到机电能量转换率随σ2变化的曲线图，如图6 所示。PBAVEH 的机电能量转换率基本不随σ2的改变而改变;而NPBAVEH 的机电能量转换率随着σ2的变大而逐渐增加，最后趋于平缓。当σ2＜1.1 时，PBAVEH 的机电能量转换率较高;而当σ2＞1.1 时，NPBAVEH的机电能量转换率较高。

图6 随σ2 变化的机电能量转换率图

取σ2=0.5 时，NPBAVEH 与PBAVEH 无量纲响应x的时域图如图7 所示。由于激励的能量较小，NPBAVEH 的响应还在单个势阱中做小幅振荡。取σ2=2.5 时，NPBAVEH 与PBAVEH 无量纲响应x的时域图如图8 所示，NPBAVEH 的响应不断在两个势阱中跃迁振荡。无论σ2取多少，PBAVEH 的响应都只是在单个势阱中，而随着σ2的增大，激励的能量输入越来越高，使得NPBAVEH 的响应从单个势阱中做小幅振荡逐渐变为在两个势阱中大幅度跃迁振荡，最终使得NPBAVEH 机电能量转换率逐渐升高。

图7 σ2 =0.5 时NPBAVEH 与PBAVEH 的响应x 时域图

图8 σ2 =2.5 时NPBAVEH 与PBAVEH 的响应x 时域图

3 结论

为了提高压电能量收集器的输出性能，笔者设计了一种新型非线性压电阵列式能量收集器，该能量收集器将压电悬臂阵列排布，并将悬臂梁的输出电压串联。增加两个永磁铁对结构进行改进，建立系统的机电耦合模型，通过输入白噪声激励，并从输出功率和机电能量转换率的角度，与线性压电阵列式能量收集器进行仿真对比。仿真结果表明，在激励强度较大时，相对于线性压电阵列式能量收集器，所设计的该压电能量收集器有效提高了输出功率和机电能量转换率。

［1］ BOZIDAR M.Piezoelectric wide -bandwidth vibration energy harvester-smart Sand［D］.Yale：Yale University，2011.

［2］ 刘祥建，陈仁文.压电振动能量收集装置研究现状及发展趋势［J］.振动与冲击，2012，31(16)：169-176.

［3］ 王青萍.基于压电悬臂梁的振动能量收集器的研究［D］.武汉：华中科技大学，2011.

［4］ ERTURK A，INMAN D J.Broadband piezoelectric power generation on high-energy orbits of the bistable duffing oscillator with electromechanical coupling［J］.Journal of Sound and Vibration，2011，330(10)：2339-2353.

［5］ 崔岩，王飞，董维杰，等.非线性压电式能量采集器［J］.光学精密工程，2012，20(12)：2737 -2743.

［6］ STANTON S C，OWENS B A M，MANN B P. Harmonic balance analysis of the bistable piezoelectric inertial generator［J］. Journal of Sound and Vibration，2012，331(15)：3617 -3627.

［7］ 佘引，温志渝，赵兴强，等.MEMS 压电阵列振动能量收集器［J］.传感技术学报，2014，27(8)：1033-1037.

［8］ WEN Z Y，DENG L C，ZHAO X Q，et al. Improving voltage output with PZT beam array for MEMS-based vibration energy harvester：theory and experiment［J］.Microsystem Technologies，2015，21(2)：331 -339.

［9］ 陈定方，孔建益，杨家军，等.现代机械设计师手册［M］.北京：机械工业出版社，2014：1326 -1328.

［10］ 孙舒.双稳态压电悬臂梁发电系统的动力学特性研究［D］.天津：天津大学，2013.

［11］ 高毓璣，冷永刚，范胜波，等.弹性支撑双稳压电悬臂梁振动响应及能量采集研究［J］. 物理学报，2014，63(9)：62 -74.