基于无源鲁棒控制的单相电弧炉 电极调节系统

赵 爽 刘小河

（北京信息科技大学自动化学院，北京 100192）

随着时代的进步，科技的发展，国家对于特种钢需求也越来越大。目前，对于特种钢的冶炼方法主要是电弧炉炼钢。由于特种钢的冶炼对于温度的稳定性要求极高，故对于电弧炉电极的稳定性以及跟踪反应能力要求极高。目前，大多数电极调节系统采用可控硅-交流力矩电机式电极调节器，其最大的优势在于电极提升速度快，反应快，能更好的应变电弧炉炼钢时出现的随机性问题[1]。

近年来，很多学者将非线性控制方法引入电弧炉电极调节系统。如非线性系统的微分几何方法，智能控制理论，以及模型参考自适应和反馈线性化等。非线性系统的微分几何方法主要是将控制系统的状态方程看做光滑的向量场，将所有的状态转变成状态空间而不再是一个微分流行。智能控制方法中包括模糊控制和神经网络控制，然而，智能控制方法是通过模仿人的思维过程建立的，对于复杂多变的系统，不能及时有效的改变，反应能力较差。模型参考自适应和反馈线性化是当今理论比较成熟、应用广泛的算法，但是在抑制外界抗干扰方面不是很好，所以在实际工业中难以应用[2]。

故本文将无源鲁棒控制方法应用于电弧炉电极控制系统，该方法是一种构造性方法，它利用系统的结构特性构造出整个系统的存储函数，当存储函数满足耗散不等式时，系统稳定，为了增加系统的抗干扰性以及灵活性，故又加入了鲁棒控制理论，所以系统控制器的设计过程有较强的系统性、灵活性和结构性，而且保留系统中有用的非线性项。

1 电弧炉系统描述

三相电弧炉电极调节系统是一个存在强耦合的复杂系统。为了简化三相电弧炉电极调节系统的复杂性，本文从单相电弧炉开始研究，为三相电弧炉理论研究打下基础。单相电弧炉电极调节系统主要由整流滤波环节、比较器、调节器以及执行机构组成。其中，整流滤波环节用来将检测的主电路电压、电流信号变换为相应电平的直流信号，比较器将转换成的直流电压信号与给定输入进行比较，它们的差值信号通过调节器进入触发回路来控制晶闸管整流电压，由这个电压控制的直流或交流电动机来带动机械传动机构，使电极上下移动来调节电弧长度，维持电弧电流和电压在某一个设定值上。为使系统稳定运行，通常引入速度反馈环节可以使系统稳定运行[3]。

在电弧炉电极调节系统中，电极调节器可以用线性传递函数来描述，如图1所示。其中执行机构主要由伺服电机完成。电弧炉主电路可视为一个将电弧弧长映射为电弧电流的非线性环节。根据数据可以理想的认为是一个反比例函数，其非线性函数关系可表示为

式中，L为电弧弧长，I为电弧电流，为常数，u是待定的控制信号，z代表电弧电流输出，为电弧弧长，y为滤波后的电弧电流输出[4]。

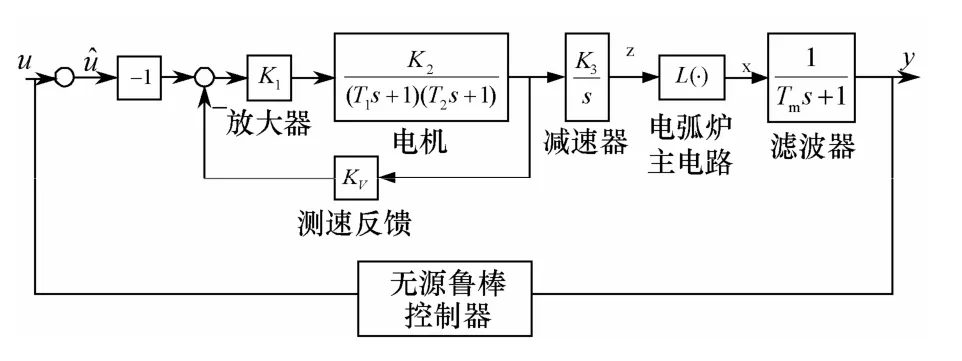
图1 基于无源鲁棒理论的单相电弧炉电极 调节系统框图

对于电弧炉这个复杂的非线性系统，为了更好的控制，本文须先将其线性化。线性化过程如下，由各状态变量之间传递函数的表达式可得

将放大器、电机、减速器、速度反馈，构成内环传递函数 ()sφ：

在前项通路中，由图可得

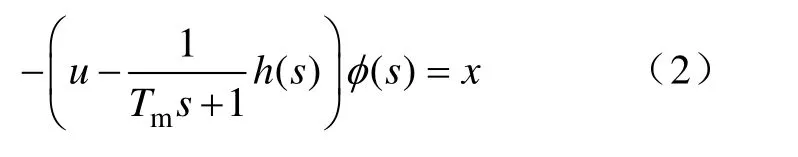
代入内环传递函数φ(s)，变形，化简可得

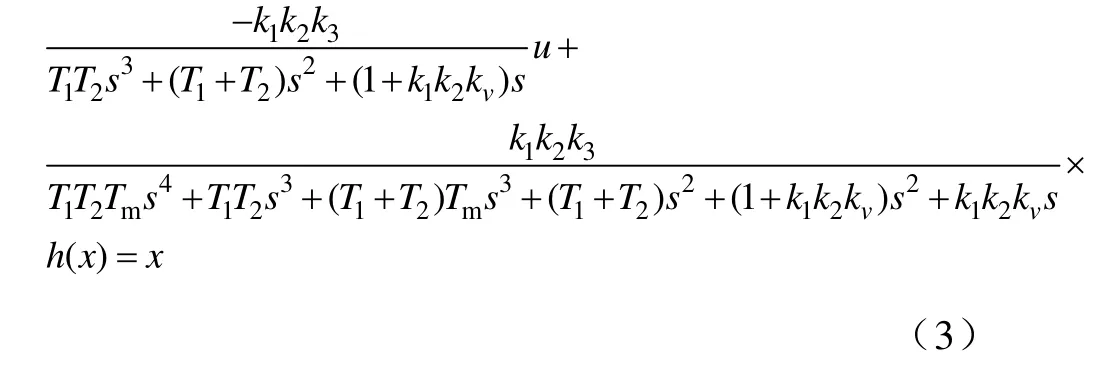
进一步整理，两边同取反拉氏变换得

代入公式（4）可得

系统可写成相应的仿射非线性系统的形式如下：

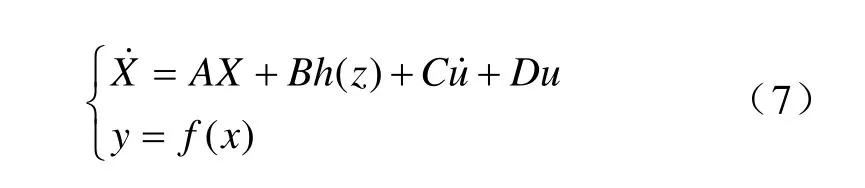
2 电弧炉电极调节系统的无源鲁棒控制

无源性理论是耗散性理论的一个特例。无源性概念经Kalman、Popov、Yakuboeieh、willems、Moylan 以及Hill 等著名学者的发展，形成了系统的无源性理论，现己成为控制理论研究的重要分支。但由于无源控制理论相对阶为1 的限制，无源控制理论很难单独应用于复杂系统，故需要鲁棒控制方法与其结合。近年来，该方法也被许多学者用于各个控制领域，并得到了很好的结果[5]。

对于一个系统，如果我们能定义一个表示能量的正定函数，使得其值为零的充分必要条件是该系统的所有状态变量均为零，且其值始终小于外界能量输入的总和，那么该系统就是稳定的。无源性的概念就是基于这种思路来考察系统自身的稳定性和对外界输入的响应的。若系统的能量总是小于或等于初始时刻系统所具有的能量与外部提供的能量之和，那么这类系统就成为是无源的。

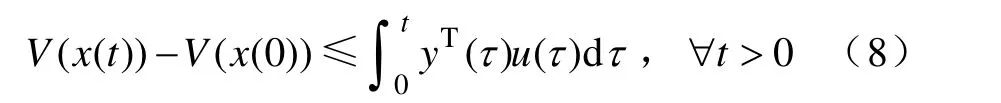
对于系统，若存在正定的函数V(x)，使得 对任意的输入信号u∈ Rn都成立，则称系统是无源的，V(x)称为能量存储函数。

对于无源系统和能量存储函数V(x)，若存在正定函数Q (x)，使得无源不等式

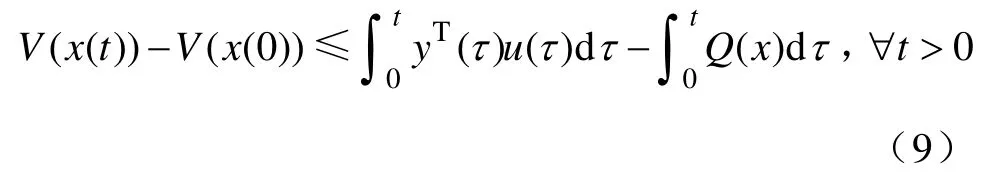
对任意的输入信号u∈ Rn都成立，则称该系统是严格无源的。

无源鲁棒控制的基本思路是将非线性系统分解成不超过系统阶数的子系统，然后为每一个子系统设计构造函数，并一步步反推到整个系统，算出存储函数使其满足严格无源定理，最终得到控制律U。无源鲁棒控制不仅适用于线性系统，也适用于具有参数不确定的非线性。

无源鲁棒控制理论设计如下考虑如下系统：

式中，x∈Rn为状态变量，y∈R表示输出变量，η(x,t)表示有界的扰动，u∈R表示控制率，θ= (θ1,θ2…θm)T表示不确定扰动，φi(x)，ξ(x)为光滑矢量场。

第一步：设理想状态输出变量(x)，实际输出变量xi(x)。

那么

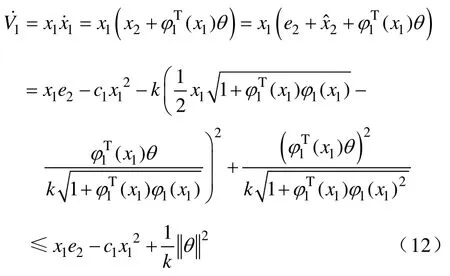
定义：x1=e1

代入式（12），可得

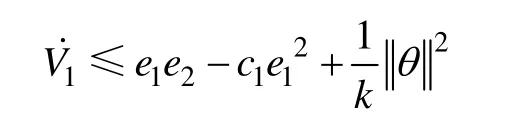
第二步：

根据式（13）、式（14）得

则

代入得

定义：

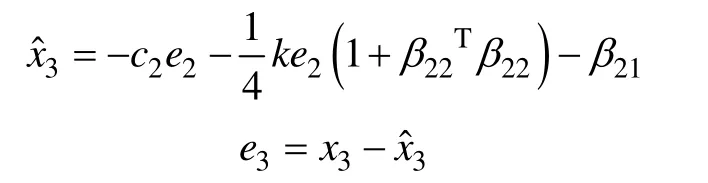
代入得

第i步：同理可得

第n步：

根据电弧炉特性以及前人的实验证明，令

式中，Δx为弧长扰动，主要是由于实际工业中，钢水的沸腾造成的。η为进入电弧炉主电路的外加扰动，主要是电极之间的耦合造成的。

将上述方法，代入到单相电弧炉电极调节系统：

代入公式得

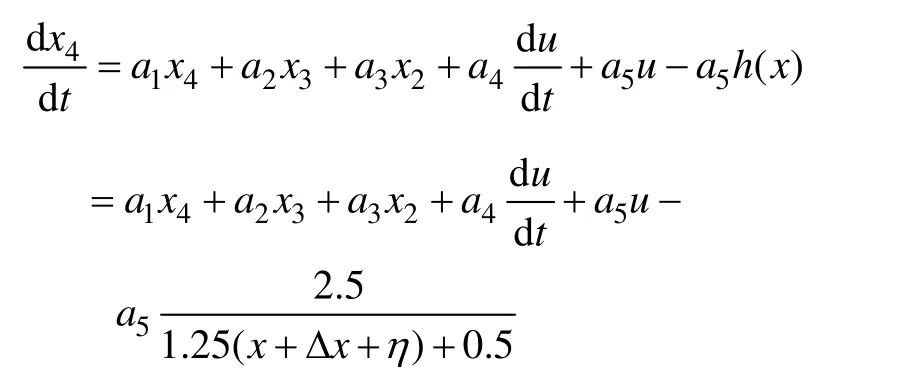
根据泰勒级数展开式，令Δx=Qx1，Q∈(-0 .2,0.2)，η=w(t)将h(x)展开得

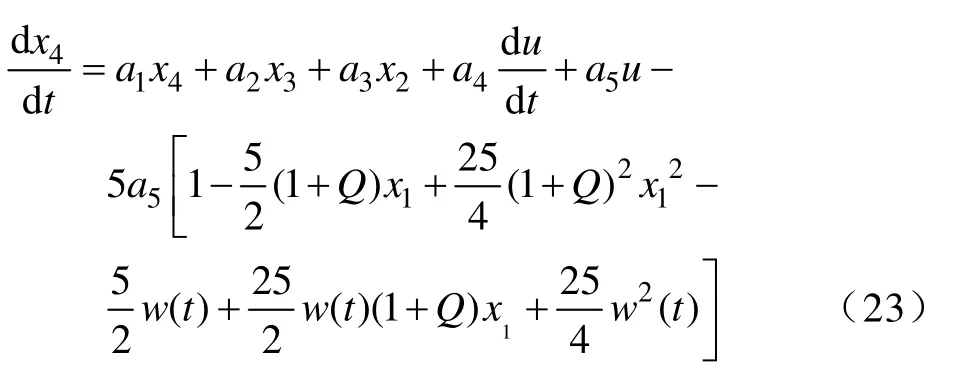
其中：

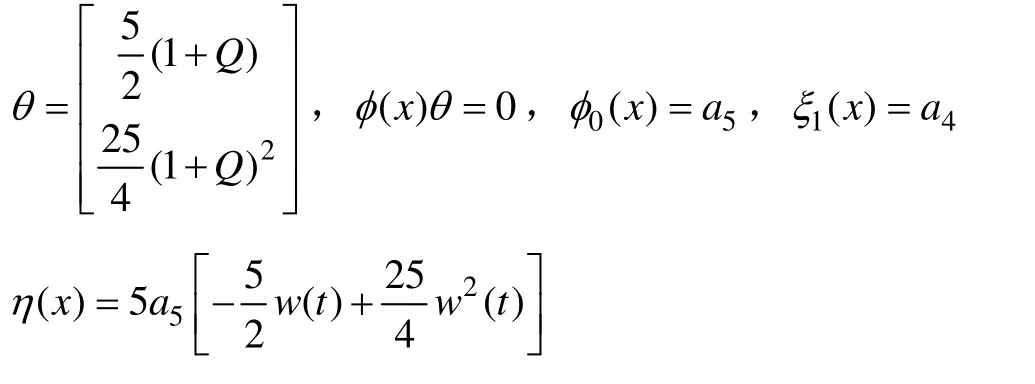
最终的控制率为

3 Simulink 仿真

经过仿真调试和前人的经验设置各参数数值如下：

3.1 搭建Simulink 仿真图

如图2、图3所示。

图2 基于无源鲁棒控制的单相电弧炉仿真图

图3 无源鲁棒控制模块图

3.2 模拟结果

根据搭建的模拟图，运行Simulink，结果如图4所示。

图4 基于无源鲁棒控制理论的仿真结果

仿真实验表明：基于无源鲁棒理论控制方法，可以适用于电弧炉电极调节系统，通过单相电弧炉电极调节系统模拟结果可以看出，调节过程较短，超调量较小，跟踪效果良好，对弧长扰动抑制效果好，为实现基于无源鲁棒控制法的三相电弧炉电极调节系统控制，打下基础。

4 结论

本文介绍了将无源鲁棒控制应用于电弧炉电极调节控制系统的推导过程，并验证了对电弧炉电极调节系统的控制效果。结果表明该控制方法具有很好的跟踪性能，且对弧长扰动产生的影响有很好的抑制能力。该仿真结果为研究新一代的电弧炉电极调节系统提供了全新的研究思路和方案。在以后作者将继续研究基于无源鲁棒的控制器三相电弧炉电极调节系统。

[1] 吴定高.我国电弧炉炼钢的发展[J].广州化工,2013,41(12): 63-65.

[2] 李磊,毛志忠.基于近似模型的电弧炉解耦控制器[J].控制理论与应用,2013(1): 101-110.

[3] 刘小河.电弧炉电气系统的模型、谐波分析及电极调节系统自适应控制的研究[D].西安: 西安理工大学,2000.

[4] 陈庆.电弧炉自适应伪微分反馈电极控制器的设计[J].电工电气,2011(6): 22-24,45.

[5] 曾蓉.基于无源性理论的状态反馈控制[D].哈尔滨: 哈尔滨理工大学,2009.

[6] Taslimian M,Shiraz Univ,Shiraz Iran,et al.Fuzzy type-2 electrode position controls for an Electric Arc Furnace[J].Information Reuse and Integration(IRI),2012 IEEE 13th International Conference on.8-10 Aug.2012.498-501.

[7] 花皑,王莉莎,王华,等.实时跟踪过程参数式电弧炉电极调节系统[J].工业加热,2013,42(1): 1-4.

[8] 于丰,毛志忠.电弧炉系统电弧模型的建立与参数辨识[J].东北大学学报(自然科学版),2013,34(2): 178-181.

[9] Mirkin B,Gutman P O.Robust Output-Feedback model reference adaptive control of SISO plants with multiple uncertain,Time-Varying state delays[J].Automatic Control,IEEE Transactions on,2008,53(10): 2414-2419.

[10] 朱贺,韩星,姜子晴.电弧炉电极调节器的参数自整定[J].工业加热,2013,42(1): 18-20.

[11] Mohammad-Hoseini S,Farrokhi M,Koshkouei A J.Robust adaptive control of uncertain non-linear systems using neural networks[J].International Journal of Control,2008,81(8): 1319-1330.