电流互感器取电的最大功率点跟踪 控制算法的研究
徐质彬 王 武
(福州大学电气工程与自动化学院,福州 350116)
随着智能电网的发展,电力系统在线监测变得越来越重要。通常有三种方式给这些监测设备供能,分别是光伏发电供能、电流互感器(CT)取电供能、分压电容取电供能。光伏发电的控制电路相对简单,但PV 电池对于环境的变化非常敏感,并且需要备用电池[1];通过分压电容取电利用高压导线对地分布电容来取电,该方法需要隔离取电电路和后续电磁兼容设计并且输出的功率有限;对于一般的CT取电,对于一次侧电流的较大变化下,无法稳定的输出功率[1-4]。
本文针对以上不足,根据文献[5]中P-I 波形,在实际的CT 取电系统中,加入MPPT 控制策略,通过调整控制器的占空比,改变负载的等效阻抗,使得其始终与电流互感器的匹配阻抗等效,从而实现CT 取电的最大功率点的跟踪。
1 CT 取能的模型
传统的CT 取电模型,它包括铁心、取能线圈、二次侧负载等,如图1所示。文献[6]所述的二次侧输出通常输出是使用阻性负载,其输出的电压是一个正弦波。然而实际二次侧输出所连接的是一个整流后的负载。这种差异导致了CT 取电模型的不准确性。

图1 CT 取电原理图及改进的CT 取电的原理
文献[7]在CT 取能模型的负载侧加入容性与感性的负载。本文在传统的CT 取电模型上引入整流桥及电容器,提高了CT 取电模型的准确性,如图2所示。然后本文对CT 取电模型中的磁芯结构、电容电压、负载等相关参数分流的波形如图3所示。输出电压u(t)与im(t)的波形如图4所示。
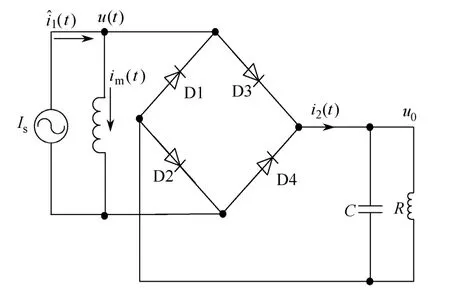
图2 简化电路

图3 临界电流的波形
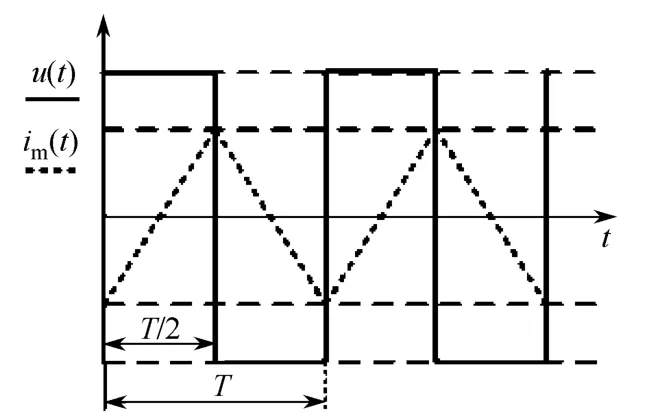
图4 u(t)与im(t)的波形
析研究,根据文献[8]对CT 取电模型的参数关系的数学公式的推导,加入MPPT 控制策略以获得最大的功率输出。
将图1中的参数换算至二次侧,则得到等效电路图2。
根据互感器的磁平衡原理,可得到等式:
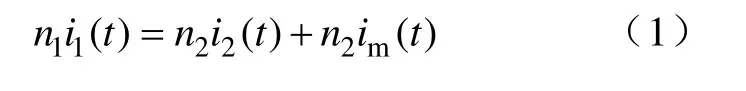
式中,n1、n2分别表示为一次侧绕组的匝数和二次侧绕组的匝数;Is是转换到二次侧的正弦电流源;Lm为励磁电感;im(t)为励磁电流;u(t)为次级绕组电压;i2(t)为全桥整流后电流;C为稳压电容;u0为负载电压;
2 CT 取电特性曲线
假设电容器C足够大:

当i2(t)=0,所有的电流都用来励磁,此时im(t) =(t),CT 取电工作在断续条件下。本文研究的重点是在当一次侧电流足够大时且磁心不处于深度饱和状态下,i2(t)始终大于零条件下的连续导通模式。(t)与im(t)临界。
由法拉第电磁感应定律可知

式中,φ、B、S分别为磁通量、磁感应强度、横截面积。
对式(3)在0 至T/2 内积分

在式(4)中,u为方波电压的绝对值,同时u也满足

由式(3)、式(4)可得

令Ip为一次侧正弦交流电的峰值,则一次侧正弦交流电Is=Ipcos(ωt+φ),其中ω周期为2πT,φ为交流电初相。由式(2)、式(3)可知,当t=0 时:
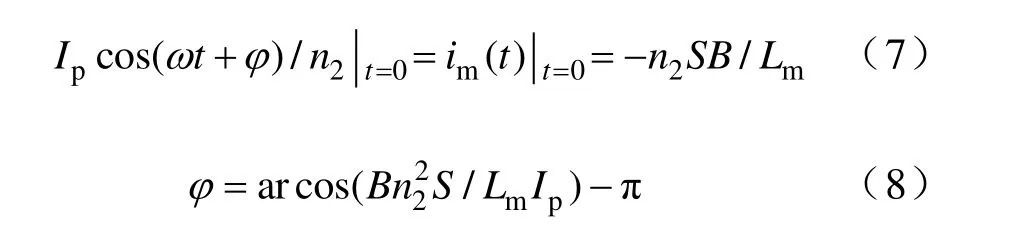
负载端一个周期内的平均电流为

忽略整流桥后的压降,该负载的平均功率PAV为

或
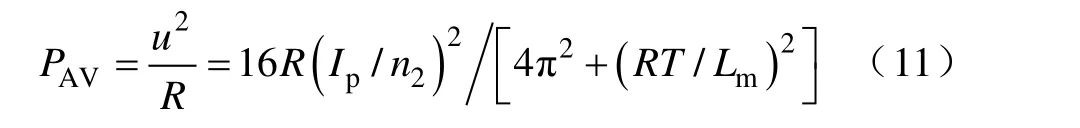
由式(10)、式(11)可得最大功率Pmax为

其中:

式中,μ为磁导率,l为磁极长度。
式(12)、式(13)、式(14)可用式(15)表示:

通过式(18)可知,电流互感器的最大功率输出与磁导率、磁极长度、横截面积有关,与二次侧绕组匝数无关。
将上式转化为工程化数学模式,加入适当补偿因子。可建立CT 取电的软件仿真模型。该模型通过Simulink 仿真,并且参考PSIM 软件对此模型的可行性论证,仿真结果如图5所示。
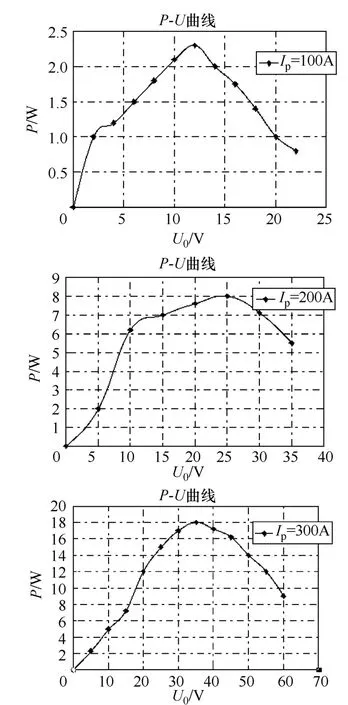
图5 一次侧电流不同P-V 曲线
从图6中可以看出:CT 取电的输出特性呈现出典型的非线性特性。输出功率与输出电压受一次侧电流变化影响很大。一次侧电流一定时,每条P-U曲线都存在最大功率输出点。输出功率随着负载电压增大而增大,达到最大功率点后开始下降,此时最大功率点Pmax即取能效率达到最高。
3 MPPT 控制机理
3.1 MPPT 算法
MPPT 扰动观察法的基本原理是在CT 取电二次侧输出电压上加一个扰动,然后观察其输出功率的变化,若功率增大,则继续正向扰动,反之则反向扰动,至追踪到最大功率点。本文提出的变步长扰动观察法是在此基础上通过不断调整扰动量Δu,将步长S设为与du/dt成正比的关系,即

通过控制占空比来实现MPPT,即
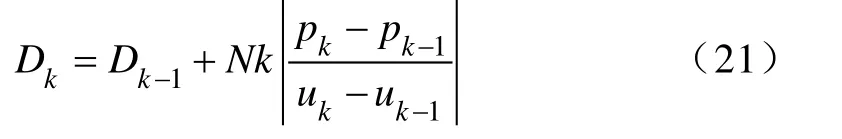
式中,N=±1 。当距离最大功率点较远时,选取较大步长,保证其快速性,当距离最大功率点较近时,选取较小的步长,保证其稳定性,抑制波形振荡。流程图如图7所示。
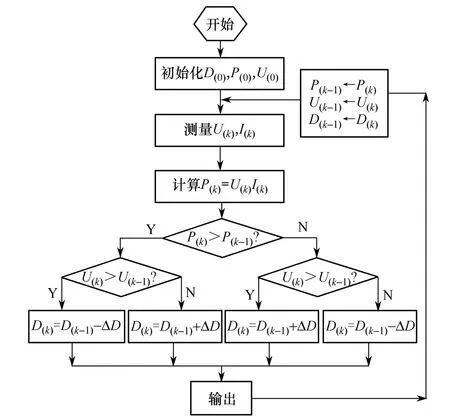
图6 变步长MPPT 流程图
3.2 系统控制电路
由于一次侧高压输电线的电流是不断变化的,为了能保持在CT 取电的最大功率点输出。本文在现有的CT 取电模型中加入最大功率点跟踪的算法。通过调整Buck-Boost 电路的PWM 占空比来调节输出电压,进行负载阻抗匹配,使得CT 取电工作在最大功率点。文中设计的控制结构如图7所示。

图7 基于Boost-buck 的MPPT 控制系统
前级Boost 电路将输入电压升高,使得后级电路能获得更多的能量而且能防止磁心深度饱和;后级Buck 电路,减小电压纹波。另一方面,对后续的负载供能提高稳定性。
3.3 系统仿真实验与分析
在Matlab/Simulink 下建立CT 取电仿真模型,系统工作在连续模式下。设Boost 变换器开关频率fs=20kHz,主电路负载50Ω,使占空比从0~1 变化。当t=0.12S时电流从70A 突变到100A。图中曲线分别为CT 取电实际输出功率P,输出电压u,输出电流i的仿真波形。由仿真波形可以看出,在系统运行中,变量P、u、i的变化均与理论分析相一致。当一次侧电流发生变化时,CT 取电系统能够实时确保最大功率点的跟踪,在最大功率点附近系统有微幅振荡。

图8 仿真波形
4 结论
针对传统的电流互感器取电的物理数学模型不足的地方,加以改进。并且根据输入电流的波形推导出输出功率与电压的数学关系式。并且通过实验仿真出CT 取电的P-U特性曲线,通过P-U曲线的特性对CT 取电的输出功率运用MPPT 算法。设计Boost-Buck 两级电路实现MPPT。从仿真结果看运用该算法提高了CT 取电的输出功率,并有效抑制电压纹波,提高输出电压稳定性。
[1] Andrew C.Corney.Simple Absolute Method for Current Transformer Calibration.IEEE,transactions on Instrumentation and measurement,2001,50(2): 278-281.
[2] Jae Kap Jung,Jeon Hong Kang,Sang Hwa Lee,et al.A New Method for Calibrating Standard Current Transformers up to 20kA.Meas.Sci.Technol,2007(11): 3309-3315.
[3] Ali Hooshyar and Majid Sanaye-Pasand,CT Saturation Detection Basedon Waveform Analysis Using a Variable-Length Window IEEE Trans.Power Del.,vol.26,no.3,pp.2040-2-50,2011.
[4] 刘亚东,王葵,陈家伟,等.基于相角控制法的电流互感器取电电源设计[J].电力系统自动化,2011,35(19): 72-75.
[5] 刘亚东,王又佳,陈静,等.基于功率控制法的电流互感器取电电源设计[J].电力系统自动化,2010,34(3): 70-74.
[6] Yuwei Shang,Huayang Li,Jinhua Wang,Jiande Wu,Xiangning He “Analysis and Design of a Current Transformer Fed Power Supply from High AC Voltage Cable.sponsored by the NationalNatureScience Foundation of China IEEE,2012: 177-182.
[7] 周健瑶.结合超级电容和锂电池的电流互感器取能电源研究[D].重庆: 重庆大学,2013.
[8] 李志先,杜林,陈伟根,等.输电线路状态监测系统取能电源的设计新原理[J].电力系统自动化,2008,32(1): 76-80.

