关于一类图的邻点可区别全染色*
胡凤凤,刘家保
(1.安徽大学数学科学学院,合肥 230601;2.安徽新华学院公共课教学部,合肥 230088)
关于一类图的邻点可区别全染色*
胡凤凤1,刘家保2
(1.安徽大学数学科学学院,合肥 230601;2.安徽新华学院公共课教学部,合肥 230088)
图G的一个正常全染色f称为是邻点可区别的,如果G中任何相邻点及其关联边的颜色集合不同;对一个图G进行邻点可区别的正常全染色所用最少颜色数称为G的邻点可区别全色数,记为 χat(G);给出了一类特殊图类的邻点可区别全色数.
正常全染色;邻点可区别全染色;邻点可区别全色数
具有重要实际意义和理论意义的图的染色问题,是图论的主要研究内容之一.随着图的染色问题在现实中被广泛应用,它逐渐成为众多学者研究的重要领域之一.起源于网络问题、生物学、信息科学、计算机科学的点可区别边染色或强边染色是一个十分困难的问题.在文献[1,2]中,点可区别边染色和邻点可区别边染色问题得到进一步研究.张忠辅教授在文献[3]中提出邻点可区别全染色的概念.新的染色问题不断被提出,与该问题相关的文献[3-9]中给出了邻点可区别染色、邻点可区别强全染色等染色的定义及其几类简单图关于此染色的色数,并提出了一些猜想.此处所考虑的图都是有限简单无向图,用V(G),E(G)分别表示图G的顶点集、边集,Δ(G)表示图G的最大度,所用的未说明的图论术语与记号参见文献[9].
1 相关定义
定义1[3]设图G是阶至少为2的连通图,k是正整数,f是V(G)∪E(G)到{1,2,…,k}的映射,∀u,v∈V(G),记C(u)={f(u)}∪{f(uv)|u,v∈V(G),uv∈E(G)}.
如果对∀uv,vw∈E(G),u≠w,有f(uv)≠f(vw);对任意uv∈E(G),有f(u)≠f(v),f(u)≠f(uv),f(v)≠f(uv),则称f为图G的k-正常全染色;进一步,如果f还满足对任意uv∈E(G),有C(u)≠C(v),则称f为图G的k-邻点可区别全染色(简记为k-AVDTC),称min{k|G有k-邻点可区别全染色}为图G的邻点可区别全色数,记为χat(G),其中C(u)称为点u在f下的色集合.
定义2[10]设图是由长为h的路连接一个m星图中心和一个n星图的中心所得到的图,其中:
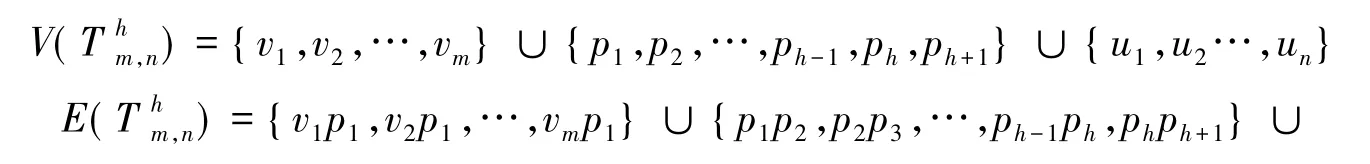
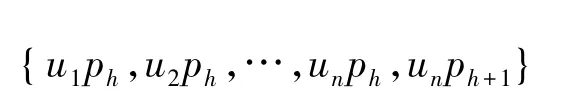
2 引 理
引理1 若G有两个相邻的最大度顶点,则
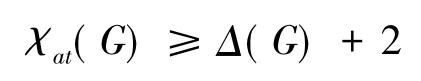
证明 设u,v是G中相邻的两个最大度顶点,则对于G的任意一个k-邻点可区别全染色f来说,C(u)和C(v)均有Δ(G)+1种颜色,而C(u)≠C(v),因此要使G有k-邻点可区别全染色,必有k≥Δ(G)+2,故结论成立.
引理2[4]设Pn是n阶的路,n≥2,则
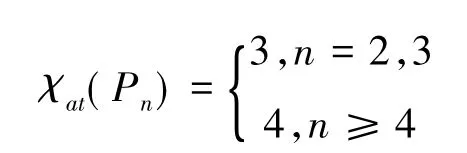
引理3[4]设Cn表示n阶圈,则
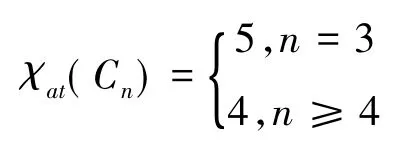
引理4[4]对于n+1阶星Sn(n≥3),有χat(Sn)=n+1.
3 主要结论及其证明

当m≠n时,有
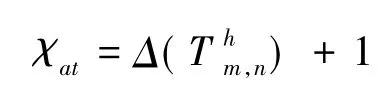
证明 分两种情况来加以讨论说明.
情况Ⅰ 1)当m=n=1,h=2时,图Thm,n就是一条4阶路,由引理2可知χaT=4.
2)当m=n且h是奇数时,定义一个从V(Thm,n)∪E(Thm,n)到{0,1,2,…,Δ(Thm,n)+2}上的映射f如下:
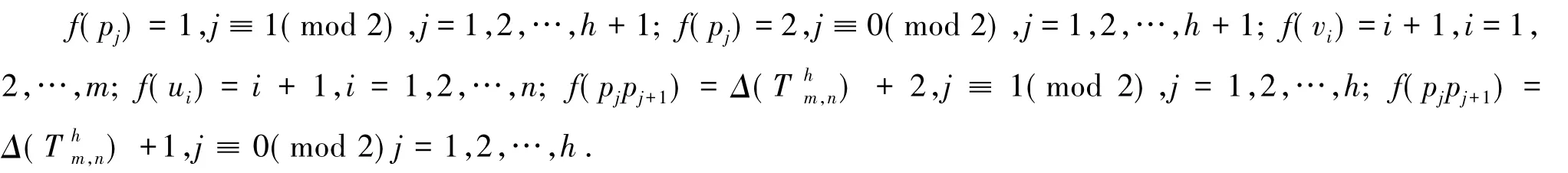
3)当m=n且h是偶数时,定义一个从V(Thm,n)∪E(Thm,n)到{0,1,2,…,Δ(Thm,n)+1}上的映射f如下:

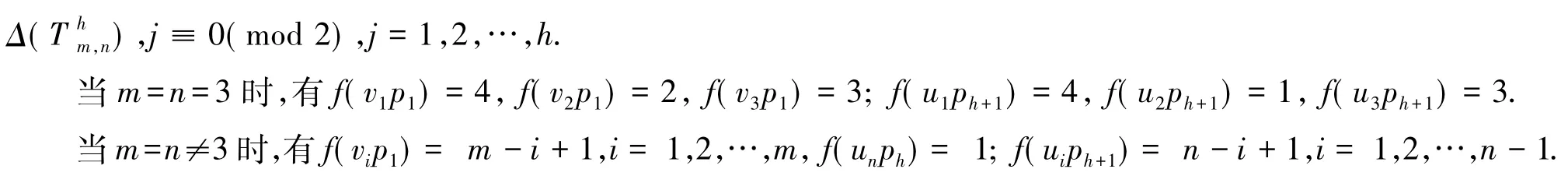
情况Ⅱ 1)当m=1,n≠1(或 m≠1,n=1)时,定义一个从到{0,1,2,…,的映射f如下:
[1]BALISTER P N,BOLLOB B,SHELP R H.Vertex Distinguishing Coloring of Graphs with Δ(G)=2[J].Discrete Mathematics,2002(252):17-29
[2]ZHANG Z F,LIU L ZH,WANG J F.Asjacent Strong Edge Coloring of Graphs[J].Applied Mathematics Letters,2002(15): 623-626
[3]ZHANG Z F.On the Adjacent Vertex Distinguish Total Coloring of Graphs[J].Science in China Ser A,2004(10):574-583
[4]刘家保,王林,陆一南.双圈图G(n,m)的奇优美标号及其算法[J].合肥工业大学学报:自然科学版,2012,35(5): 708-710
[5]刘家保,王林,陆一南.具有公共边的双圈图的奇优美标号及其算法[J].合肥工业大学学报:自然科学版,2012,35(6): 857-859
[6]张忠辅,李敬文,陈样恩.图的距离不超过β的点可区别全染色[J].中国科学A辑:数学,2006,36(10):1119-1130
[7]刘家保,邹婷,陆一南.关于笛卡尔乘积图的优美性[J].纯粹数学与应用数学,2012,28(3):329-332
[8]严谦泰.关于图的一般邻点可区别全染色[J].系统科学与数学,2010(1):101-106
[9]BONDY J A,MURTY U S R.Graph Theory with Applications[M].New York:American Elsevier,1976
[10]刘家保,吕宁宁,余国锋.关于一类树的优美标号[J].河北北方学院学报:自然科学版,2010,26(5):1-4
On Adjacent Vertex Distinguishing Total Coloring for a Class of Graphs
HU Feng-feng1,LIU Jia-bao2
(1.School of Mathematical Science,Anhui University,Hefei 230601,China; 2.Teaching Department for Common Courses,Anhui Xinhua University,Hefei 230088,China)
A normal total coloring f of graph G is adjacent vertex distinguishing.If any point of an adjacent vertex in G and the color set of its related edges are different,the smallest number of colors used in the normal adjacent vertex distinguishing total coloring for a Graph G is called the number of adjacent vertex distinguishing total coloring and is denoted as Xat(G).This paper gives a class of special adjacent vertex distinguishing total coloring number of graphs.
normal total coloring;adjacent vertex distinguishing total coloring;adjacent vertex distinguishing total coloring number
O157.5
A
1672-058X(2015)02-0023-04
10.16055/j.issn.1672-058X.2015.0002.005
责任编辑:李翠薇
2014-07-18;
2014-09-18.
安徽省高等学校省级自然科学基金项目(KJ2010B105);安徽新华学院质量工程建设项目(2012tskcx04,2012tskcx05).
胡凤凤(1990-),女,安徽蚌埠人,硕士研究生,从事图论与组合网络研究.

