负载下CFRP约束混凝土应力-应变关系分析型模型

潘 毅， 万 里， 吴晓飞

(1.西南交通大学土木工程学院，四川成都 610031;2.西南交通大学交通隧道工程教育部重点实验室，四川成都 610031)

FRP(fiber reinforce plastic)约束混凝土柱可以提高柱的强度和延性.在过去10多年中，国内外对FRP约束混凝土的应力-应变关系模型进行了大量研究.文献[1]指出，FRP约束混凝土的应力-应变关系模型大致可分为设计型模型和分析型模型.设计型模型将FRP约束混凝土作为一个整体，通过试验回归得到FRP约束混凝土的应力-应变模型.分析型模型考虑了FRP与混凝土柱的受力平衡和应变协调条件，物理意义明确，更适用于FRP约束混凝土的非线性分析.文献[2-5]基于Mander等提出的箍筋约束混凝土的应力-应变关系[6]，用迭代方法得到了FRP约束混凝土的轴向应力-应变关系;文献[7]根据八面体强度准则提出了FRP约束混凝土峰值应力的计算方法;文献[8-9]根据大量试验数据，对FRP约束混凝土的轴向-侧向应变关系进行了修正.然而，这些研究大多针对混凝土无负载的情况，而负载会造成FRP的拉应变滞后，降低FRP的侧向约束力，最终导致FRP约束混凝土的峰值应力和峰值应变下降.

本文在试验研究的基础上，对负载下CFRP(carbon FRP)约束圆形、方形截面混凝土柱的峰值应力、峰值应变进行了修正，并根据文献[8-9]提出的主动约束方程，采用增量迭代方法，引入等效圆的概念，建立了负载下CFRP约束混凝土圆形截面柱和方形截面柱的应力-应变关系分析型模型，模型计算结果与试验结果吻合较好，可以有效考虑负载水平对CFRP约束混凝土柱的影响.

1 负载下的峰值应力和峰值应变

文献[2-5]都采用Mander等提出的箍筋约束混凝土模型[6]模拟FRP约束混凝土柱，但钢材为弹塑性材料，FRP为线弹性材料，FRP约束混凝土柱的受力情况不同于箍筋约束混凝土柱.文献[8-9]通过回归分析提出了更适合FRP约束混凝土柱峰值应力和峰值应变的表达式，可以较好地模拟FRP约束混凝土圆柱的峰值应力和峰值应变，但只能用于圆形截面，且没考虑负载水平(预加荷载与未包裹碳纤维混凝土柱破坏荷载之比)对FRP约束混凝土柱峰值应力和峰值应变的影响.

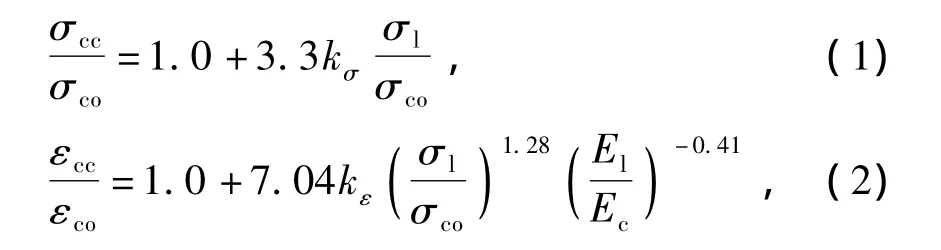
试验发现，负载水平会降低CFRP约束混凝土圆柱和方柱的峰值应变和峰值应力[10-11]，且降低幅度是负载水平的函数.基于试验数据回归分析提出的负载下CFRP约束混凝土圆柱峰值应力和峰值应变分别为[10]式中:σl为FRP提供的侧向约束力;σco和σcc分别为不考虑FRP约束和考虑FRP约束时混凝土的轴向峰值应力;εco和εcc分别为不考虑FRP约束和考虑FRP约束时混凝土的轴向峰值应变;kσ为负载下圆形截面柱峰值点的应力影响因子，kσ=(1.0-m2.3129)0.5667，其中 m 为混凝土柱的负载水平;kε为负载下圆形截面柱峰值点应变影响因子，kε=(1.0-m0.962)0.186;El为侧向约束刚度;Ec为混凝土抗压弹性模量.

图1和图2分别为根据式(1)和式(2)计算的负载下CFRP约束混凝土圆柱的峰值应力、峰值应变与试验测得的峰值应力、峰值应变的比较.可见，式(1)计算的负载下CFRP约束混凝土圆柱峰值应力的误差在10%以内，式(2)计算的负载下CFRP约束混凝土圆柱峰值应变的误差在20%以内.

图1 圆形截面混凝土柱的峰值应力Fig.1 Peak stress for circular-section concrete column

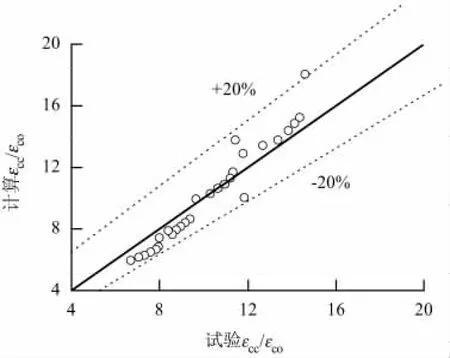
图2 圆形截面混凝土柱的峰值应变Fig.2 Peak strain for circular-section concrete column

FRP约束方形截面混凝土柱中存在非有效约束区，会造成混凝土柱侧向变形和FRP横向拉应变分布不均匀[12]，使得约束强度的计算变得复杂.引入等效圆的概念来简化CFRP约束方形截面混凝土柱中CFRP侧向约束力的计算[13]，计算得到方柱的等效侧向约束力

式中:ks为截面系数，定义为有效约束面积与方柱横截面积之比;Efrp为FRP的弹性模量;εh为FRP的拉应变;tfrp为FRP片材厚度;De为等效圆直径，定义为方形截面对角线长度.

由等效圆的概念得到CFRP约束混凝土方柱侧向应力表达式后，可根据试验数据回归得负载下CFRP约束混凝土方柱的峰值应力和峰值应变[11]:

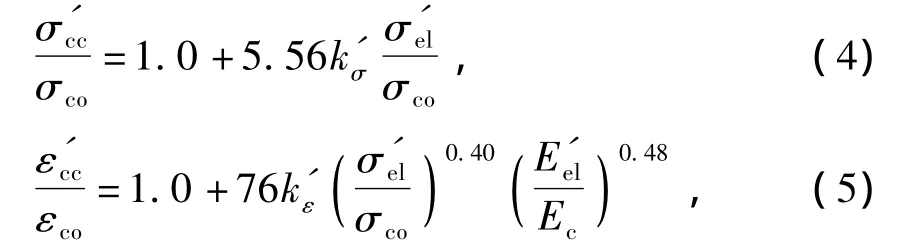
式中:k'σ为负载下方形截面柱峰值点的应力影响因子，k'σ=(1.0-m2.12)0.86;k'ε为负载下方形截面柱峰值点的应变影响因子，k'ε=(1.0-m1.36)0.28.

图3和图4分别为根据式(4)和式(5)计算的负载下CFRP约束混凝土方柱峰值应力、峰值应变与试验测得的峰值应力、峰值应变的比较.

从图3和图4可见，式(4)可以将负载下CFRP约束混凝土方柱峰值应力的计算误差控制在15%以内，式(5)可以将负载下CFRP约束混凝土方柱峰值应变的计算误差控制在15%以内.

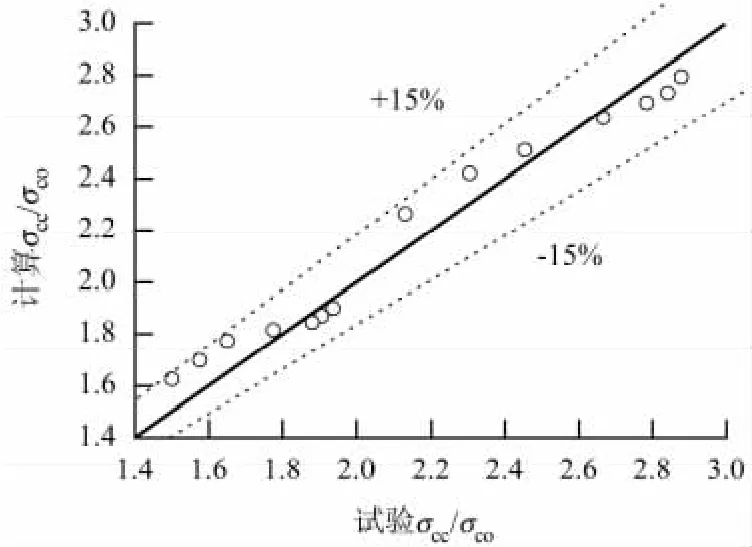
图3 方形截面混凝土柱的峰值应力Fig.3 Peak stress for square-section concrete column

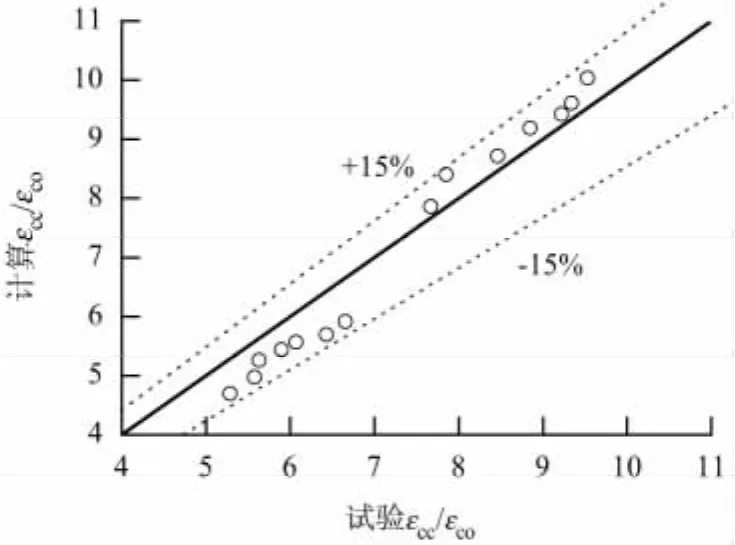
图4 方形截面混凝土柱的峰值应变Fig.4 Peak strain for square-section concrete column

求得负载下CFRP约束混凝土柱的峰值应力和峰值应变后，可根据文献[14]提出的σc-εc计算表达式(6)，得到负载下CFRP混凝土柱的轴向应力σc和轴向应变εc的关系:

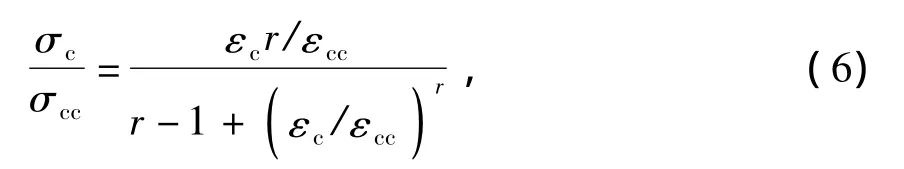
式中，r为衡量混凝土脆性的参数，r=Ec/(Ecσcc/εcc).

2 轴向-侧向应变关系计算模型

文献[14-15]对FRP约束混凝土柱割线泊松比的研究发现，极限状态下FRP约束混凝土柱的泊松比约为0.2，并根据极限状态下的泊松比近似得到FRP约束混凝土柱的侧向应变.但由于极限状态下FRP约束混凝土柱内部裂缝发育明显，用泊松比近似计算FRP约束混凝土柱的轴向-侧向应变关系不准确.文献[8-9]通过试验发现，FRP约束混凝土柱的轴向应变εc与侧向应变εl、约束比σl/σco关系密切.文献[8]给出的侧向约束时混凝土柱的轴向-侧向应变关系为

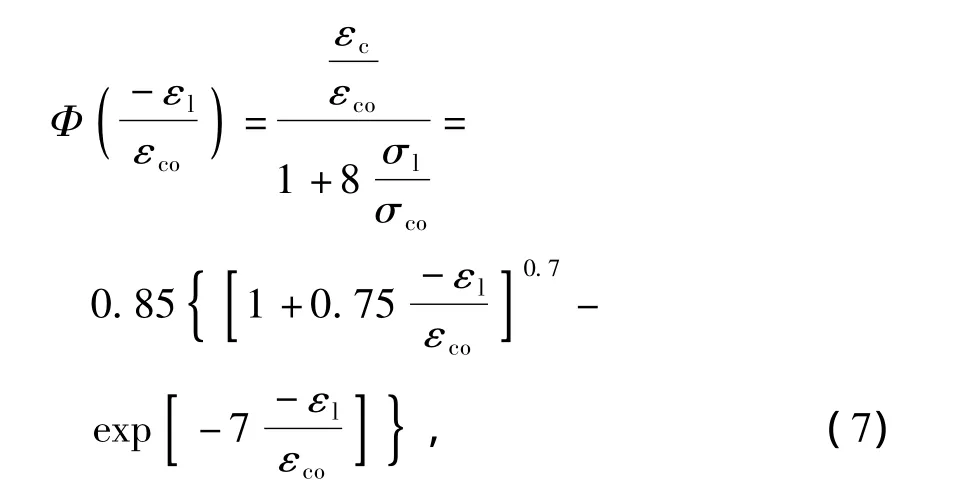
式中:εl为混凝土的有效侧向应变，它与FRP实际环向拉应变εh的关系为εl=-εh.

式(7)建立了FRP约束混凝土柱的轴向-侧向应变关系，可以有效模拟FRP约束混凝土柱的轴向-侧向应变关系[7].

3 计算步骤

根据提出的考虑负载后CFRP约束混凝土柱的峰值应力、峰值应变计算公式和基于文献[8]提出的FRP约束混凝土柱的轴向-侧向应变关系，通过迭代方法即可建立负载下CFRP约束混凝土的应力-应变关系分析模型.主要计算步骤:

步骤4 由式(1)或式(4)得到CFRP约束混凝土圆柱或方柱的峰值应力;

步骤5 由式(2)或式(5)得到CFRP约束混凝土圆柱或方柱的峰值应变;

步骤6 由式(6)得到CFRP约束混凝土应力-应变曲线上一点;

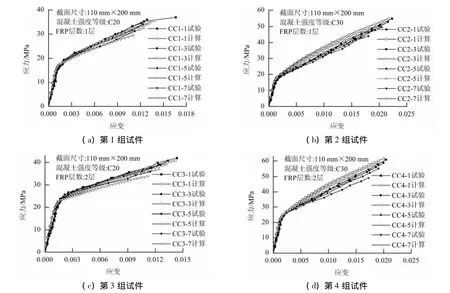
图5 FRP约束圆形截面混凝土应力-应变关系的计算、试验结果Fig.5 Numerical simulation and experimental stress-strain curves for FRP confined circular-section concrete columns

Fortran 95作为程序设计语言，在Compaq Visual Fortran 6.5编译器下开发了相应的计算程序.

4 模型验证

图5和图6分别为FRP约束的2种截面混凝土应力-应变关系的计算与试验结果(图5中截面尺寸为直径×高).负载水平相近的曲线形状大致相同，为便于比较，每组构件仅选择了4条典型曲线，负载水平分别约为 0.0、0.3、0.5 和0.7.

图6 FRP约束方形截面混凝土应力-应变关系的计算、试验结果Fig.6 Numerical simulation and experimental stress-strain curves for FRP confined square-section concrete columns

可见，不论是CFRP约束的混凝土圆柱还是方柱，提出的应力-应变分析型模型可以较好地考虑负载水平对CFRP约束混凝土应力-应变关系的影响，模拟得到的应力-应变曲线与试验结果吻合较好.此外，FRP约束圆柱的吻合程度明显好于方柱.主要是由于FRP约束方形截面混凝土柱时，尽管引入等效圆的概念能大大简化分析的复杂程度，并能高效模拟出应力-应变曲线，但很难准确反映混凝土侧向应变和FRP环向拉应变的不均匀性.另外，拐角半径、截面形状等影响因素也使FRP破坏的随机性高于FRP均匀约束下的圆柱体.

5 结论

为考虑负载水平的影响，根据试验结果，引入负载影响因子和等效圆的概念，以J G Teng本构模型为主动约束关系，建立了负载下CFRP约束混凝土应力-应变关系分析型模型，得到以下结论:

(1)提出的峰值应力影响因子和峰值应变影响因子可以较好地修正负载下CFRP约束混凝土柱的峰值应力和峰值应变.

(2)引入等效圆的概念，使提出的模型能够用于方形截面柱.方形截面柱的模拟效果不如圆形截面柱，主要是由于其侧向约束力分布不均匀.

(3)所建立的分析型模型能较准确地模拟负载下CFRP约束混凝土的应力-应变关系.

[1]TOGAY J C，THOMAS V.FRP-confined concrete in circular sections:review and assessment of stress-strain models[J].Engineering Structures，2013，49(4):1068-1088.

[2]SAMAAN M，MIRMIRAN A，SHAHAWY M.Model of concrete confined by fiber composites[J].Journal of Structure Engineering，1998，124(9):1025-1031.

[3]MIRMIRAN A，SHAHAWY M.Dilation characteristics ofconfined concrete[J]. Mechanics ofCohesive-Frictional Materials，1997，2(3):237-249.

[4]SPOELSTRA M R，MONTI G.FRP-confined concrete model[J]. Journal of Composites for Construction，1999，3(3):143-150.

[5]FAM A Z，RIZKALLA S H.Confinement model for axially loaded concrete confined by circularfiberreinforced polymer tubes[J].ACI Structural Journal，2001，98(4):451-461.

[6]MANDER J B，PRIESTLEY M J，PARK R.Theoretical stress-strain model for confined concrete[J].Structure Engineering，1988，114(8):1804-1826.

[7]王震宇，王代玉，吕大刚.FRP约束混凝土圆柱应力-应变分析模型[J].哈尔滨工业大学学报，2010，42(2):200-206.

WANG Zhenyu，WANG Daiyu，LÜ Dagang.Stressstrain analyticalmodelfor FRP-confined concrete circular column[J]. Journal of Harbin Institute of Technology，2010，42(2):200-206.

[8]JIANG T，TENG J G.Analysis-oriented stress strain models for FRP-confined concrete[J]. Structure Engineering，2007，29(11):2968-2986.

[9]TENG J G，HUANG Y L，LAM L，et al.Theoretical model for fiber reinforced polymer-confined concrete[J].Journal of Composites for Construction，2007，11(2):201-210.

[10]曹双寅，潘毅，敬登虎，等.负载下碳纤维布约束混凝土圆柱应力-应变关系的试验研究与分析[J].东南大学学报，2008，30(2):788-793.

CAO Shuangyin， PAN Yi， JING Denghu， et al.Experimentalresearch on axially loaded circular concrete columns confined by CFRP under preload[J].Journal of Southeast University，2008，30(2):788-793.

[11]潘毅，曹双寅，敬登虎，等.负载下碳纤维布约束混凝土方柱应力-应变关系的试验研究与分析[J].土木工程学报，2009，42(1):23-29.

PAN Yi，CAO Shuangyin，JING Denghu，et al.Test and analysis of the axial stress-strain relationship of square-section concrete columns confined by CFRP under preload[J].China Civil Engineering Journal，2009，42(1):23-29.

[12]ROCHETTE P，LABOSSIERE P.Axial testing of rectangular column modelsconfined with composites[J].Journal of Composites for Construction，2000，4(3):129-136.

[13]YANG X，WEI J，NANNI A.Shape effect on the performance of carbon fiber reinforced polymer wraps[J]. Journal of Composites for Construction，2004，8(5):444-451.

[14]吴刚，吕志涛.纤维增强复合材料(FRP)约束混凝土矩形柱应力-应变关系的研究[J].建筑结构学报，2004，25(3):99-106.

WU Gang，LÜ Zhitao.Study on the stress-strain relationship ofFRP-confined concrete rectangular columns[J].Journal of Building Structures，2004，25(3):99-106.

[15]SAMDANIS. Analyticalstudy ofFRP-confined concrete columns[D].Toronto:University of Toronto，2003.