不均匀地质条件下地震动目标定位方法
鲁志文, 董大伟, 华春蓉, 闫 兵, 谢 逍, 陈 俊
(西南交通大学机械工程学院,四川成都 610031)
近年来无人值守地面传感器系统(UGS)迅速发展,其在军事防入侵及民用重点区域监测等领域的前景越来越被重视.组成UGS的传感器主要有声音传感器、地震动传感器等[1-4].与声音传感器相比,地震动传感器在弱声辐射目标监测方面有一定优势[5].
目前,利用地震动传感器的目标检测及识别技术已相对成熟,但是由于地质环境的复杂性,精确的目标定位还存在较大问题[2].地震动信号目标定位的方法主要有基于到达时间(TOA)法、基于到达时间差(TDOA)法、基于到达方向(AOA)法以及基于接受信号强度(RSSI)法[6].其中,TDOA 法由于算法简单、定位精度相对较高等优点,是目前使用较广泛的方法.TDOA法的关键在于时延估计及传播速度确定.
在时延估计方面,G C CARTER等提出了广义互相关的时延计算方法[7-8];马雯等采用广义互相关法提高被动定位系统精度[9];孙洁娣等基于TDOA法对管道周边活动目标进行定位,结合HHT对提取的信号特征分量进行基本互相关时延估计[10];孟令军等基于TDOA和广义互相关相混合的方法进行目标定位,通过TDOA确定时延的大概范围,然后计算精确时延,减少了定位运算量[11].此外,基于高阶统计量[12]、互功率谱相位[13]的方法在时延估计中也有应用.
在传播速度确定方面,C W REED等将传播速度看成未知变量,通过增加传感器节点增加定位方程数,用最小二乘解定位,对于一个二维目标的定位需要6个或以上节点[14];M S RICHMAN等通过测量震源信号到达两传感器的时间差,结合传感器间距离对地震波传播速度进行估计,并以此代替整个定位区域内的传播速度[15];J G ELBRING等通过测定离传感器一系列距离的震源产生的地震动信号到达传感器的时间,根据落点规律对获得的一系列时间距离组合进行分段线性拟合,各段的斜率即为对应区域内的传播速度[16];郑惠娜通过拟合得到地震波传播速度与目标距传感器距离的非整数阶关系,并据此传播速度模型提出了改进的目标定位方法[17].
综观现有TDOA定位方法,大都假设地质条件均匀,认为传播速度恒定或者传播速度随传播距离衰减.但是实际地质环境不可能是均匀的,地震波的传播规律十分复杂,因此即使时延计算再精确,也很难保证高的定位精度.对于传播速度随传播距离衰减的假设,考虑传播过程中能量衰减造成的传播速度衰减,尽管相对于传播速度恒定的假设更符合地震动信号传播实际情况,但在不均匀地质条件下,传播速度衰减极不规律,很难拟合出传播速度与传播距离的关系.
另一方面,即使可以勉强拟合出二者的关系,也是高阶或非整数阶形式,定位求解过程相当复杂,因此也很难获得较高的定位精度.因此,寻找一种既能合理反映不均匀地质条件下地震动信号传播速度又简单实用的目标定位方法,对于提高定位精度及工程应用有重要意义.
根据三传感器TDOA法,已知目标到达传感器阵列的一对时延组及对应的传播速度,即可求出目标位置.但地质条件不均匀使得不同位置的传播速度不同,因此,获取不均匀地质条件下时延组与传播速度的对应关系,就可以实现非均匀地质条件下的目标定位.
为此,本文提出了一种基于时延-等效传播速度检索表的TDOA定位方法,将位置域的传播速度转换为时延域的等效传播速度,从而解决非均匀地质条件下的目标定位问题;对等腰直角三角形阵列的定位盲区进行了仿真分析,为消除定位盲区,采用了五元十字传感器阵列布置方式;针对某重型轮式车进行了场地试验,验证了所提方法的有效性.
1 主要理论及方法
1.1 TDOA定位基本原理
等腰直角三角形传感器阵列布置见图1.图1中,1~3为3个传感器节点,其坐标为(xk,yk),k=1,2,3.目标坐标为(x,y),则有定位基本方程:
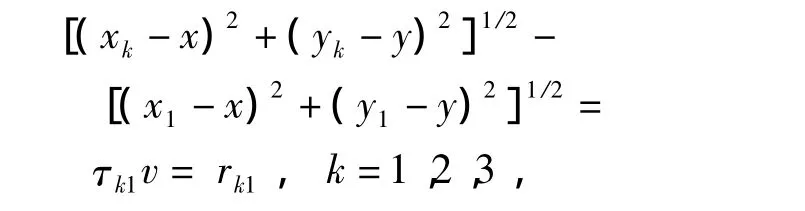
式中:τk1为目标到传感器 k与传感器1的时延;v为地震动信号传播速度;rk1为目标到传感器k和传感器1的距离差.
由CHAN算法[18]求解二元二次方程组,得
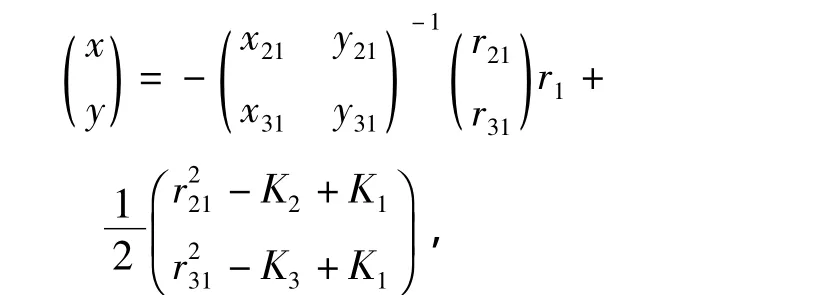
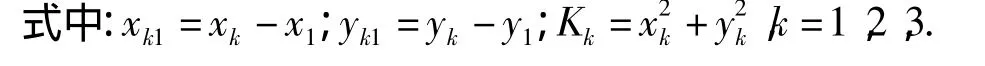
若rk1已知,则 x和 y均为 r1的函数,又 r1=(x2+y2)1/2,可得关于r1的一元二次方程 ar21+br1+c=0,取其较大根 r1=[-b+(b2-4ac)1/2]/(2a),代回即可求得 x和 y.因此,确定 rk1即可确定方程组的解,即确定目标的位置.
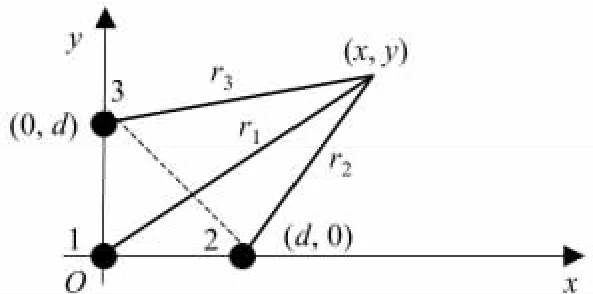
图1 等腰直角三角形传感器阵列Fig.1 Right isosceles triangle sensor array
1.2 基于时延-等效传播速度检索表的TDOA定位原理
由TDOA定位基本原理知,确定rk1即可确定目标的位置.又rk1由τk1及对应的传播速度确定,而τk1可通过传感器k和传感器1接收的地震动信号的互相关[7]运算获得.传统TDOA法中,假设地质条件均匀,认为传播速度固定,因此τk1确定则rk1确定.
然而,地质条件实际上不可能是均匀的,因此用一个常数来代替整个区域的传播速度是不合理的.但就某一具体位置的目标而言,假设时延组计算精确,尽管产生的地震动信号传播规律复杂,但总存在某个等效传播速度使得定位精确,从而可以以此等效传播速度代替时变的传播速度.
设目标位置坐标为(X(i),Y(i)),对应的时延组为(τi21,τi31),所得等效传播速度为 v(i).计算定位区域内第i个已知位置(X(i),Y(i))的时延,得到对应时延组(τi21,τi31);将传播速度在可能的速度范围内按一定步长迭代(步长由要求的传播速度的精度确定),用传统TDOA定位方法计算目标位置,并计算其与精确位置的误差,直至误差小于设定精度,即 (x -X(i),y-Y(i))2≤e,其中(x,y)为定位计算出的位置,e为设定的精度.记录收敛时的传播速度v(i)及对应的时延组(τi21,τi31),从而得到一系列时延组与传播速度的映射.为了既减少测试点数又能反映整个区域内的传播速度,采用二次插值的方法对所得的有限组映射在整个时延域内进行插值,生成时延-等效传播速度检索表,见表1.
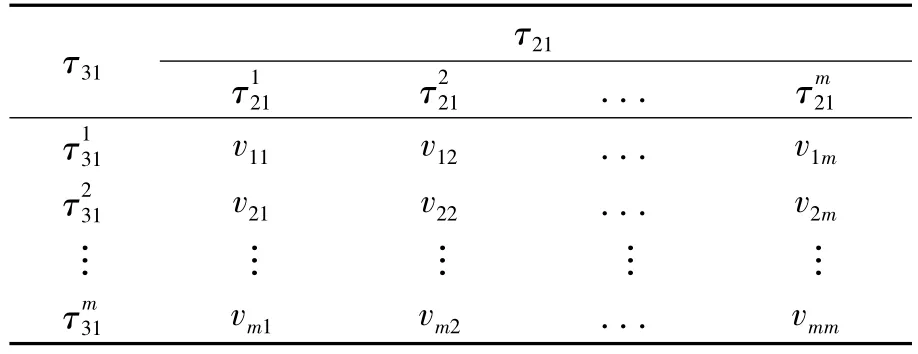
表1 时延-等效传播速度检索表Tab.1 Search table for time delay-equivalent propagation speed
表1 中,vij表示时延组(τi21,τj31)对应的等效传播速度.在后续对目标实时定位时,只需搜索时延-等效传播速度表,查找时延组对应的等效传播速度,即可得到rk1,从而实现目标定位.时延-等效传播速度检索表获取流程见图2,其中siq(t)为传感器 q 采集的第 i段数据,q=1,2,3.

图2 时延-等效传播速度检索表获取流程Fig.2 Flow chart obtaining search table for time delay-equivalent propagation speed
1.3 传感器布置方式确定及基于时延-等效传播速度检索表的TDOA五元十字阵定位的算法实现
传感器阵列对目标定位影响很大,为更好进行目标定位,首先基于固定传播速度TDOA法对等腰直角三角形传感器阵列的定位效果进行仿真分析.设传感器间距为5 m,传播速度为170 m/s,对纵、横坐标均相对传感器阵列位于-20~20 m范围内的已知点,基于TDOA法进行目标定位,此时时延是定位结果误差的唯一来源.
最理想的情况是:所有定位计算出来的点均与精确位置重合.假设时延精确,定位结果见图3,在3个顶角所夹区域无法定位,存在定位盲区;考虑5%的时延误差,定位结果见图4,斜边外法线所在象限定位精度相对较高.图5为两对顶布置的等腰直角三角形定位结果,除了直角边所在直线无法定位外,基本覆盖了整个定位区域.图3~5中,实心点为实际定位点,空心圆为待定位区域内的点.考虑时延误差,各直角三角形斜边外法线所在象限定位精度相对较高.

图3 等腰直角三角形定位盲区Fig.3 Localization ambiguity area with a right isosceles triangle sensor array
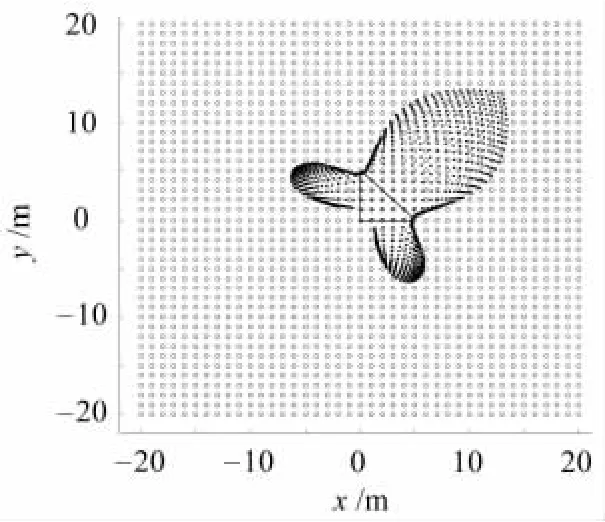
图4 时延误差5%时,等腰直角三角形定位结果Fig.4 Localization results with a right isosceles triangle sensor array when time delay has an error of 5%
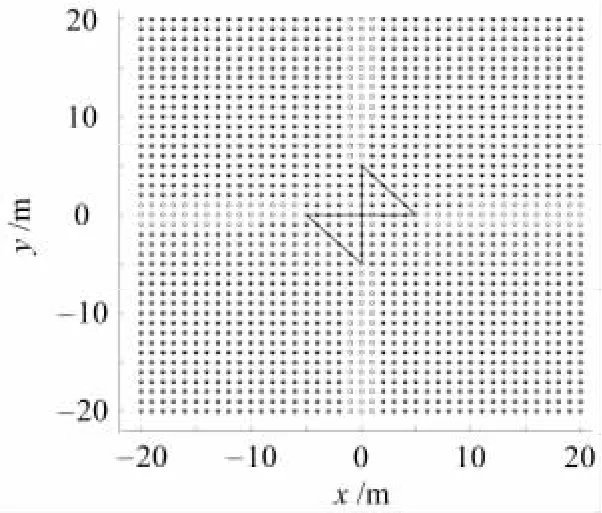
图5 五元十字阵消除盲区Fig.5 Localization ambiguity area elimination using a five-sensor cross array
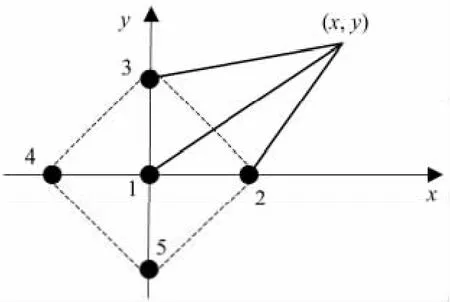
图6 五元十字传感器阵列Fig.6 A five-sensor cross array
为了消除盲区,提高定位精度,提出了五元十字阵传感器布置方式.如图6,利用形成的4个等腰直角三角形阵列对相应象限的目标进行定位.此时,关键在于目标所在大概方位的判断,从而选择对应的直角三角形阵列进行目标定位.
假设地震动信号传到远端传感器的时间长于近端传感器,则可根据传感器2和4与传感器3和5的时延判断目标的大概方位.当τ24≤0时,目标位于右半平面;当τ24>0时,目标位于左半平面.同理,当τ35≤0时,目标位于上半平面;当 τ35>0时,目标位于下半平面.但对于地质条件极不均匀的情况,可能出现个别位置不满足假设条件,因此,实际布置传感器阵列时,应尽量选择地质条件较好的场地.
按图2所示流程确定时延-等效传播速度检索表后,对运动目标的定位主要有以下内容:(1)确定目标所在象限,选择相应的定位传感器;(2)计算对应传感器的互相关时延;(3)查找时延-等效传播速度检索表,获取等效传播速度;(4)基于TDOA定位.定位算法实现流程见图7(sim(t)为传感器 m 采集的第 i段数据,m=1,2,3,4,5).

图7 基于时延-等效传播速度检索表的TDOA五元十字阵定位算法流程Fig.7 Flow diagram of TDOA based algorithm using five-sensor cross array and time delay-equivalent propagation speed search table
2 试验
2.1 地震动信号采集
为了验证基于时延-等效传播速度检索表的TDOA定位算法的有效性,进行了场地试验.运动目标为某重型轮式车,车辆沿道路中间以不同档位匀速直线行驶,距中间传感器13.5 m;地震动传感器采用五元十字阵方式布置,传感器间距5.0 m,见图8.采集的地震动信号的主要频率成分集中在150 Hz内.在满足采样定理的同时,为了减小数据点数过少带来的时延计算误差,信号采样频率设定为2 048 Hz.图9为传感器1采集的地震动信号.

图8 场地定位试验布置Fig.8 Arrangement of field localization experiment
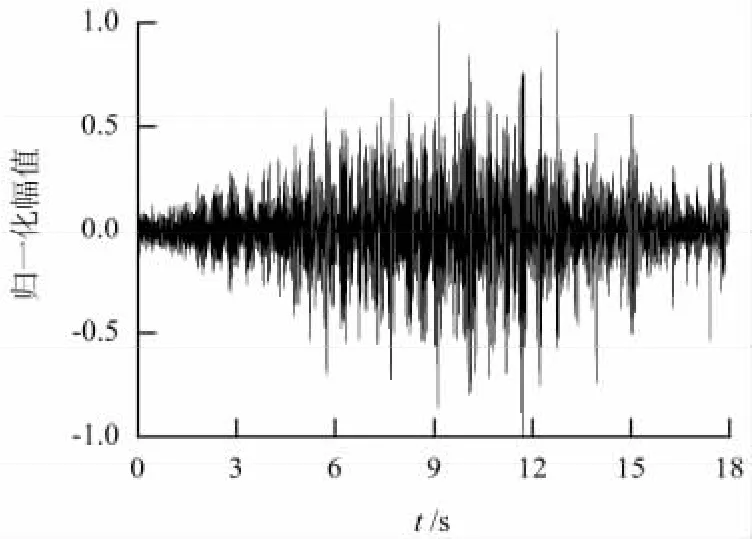
图9 传感器1采集的地震动信号Fig.9 Seismic signal collected by No.1 sensor
2.2 时延-等效传播速度检索表的计算
按图2流程,对各传感器采集的地震动信号进行处理.首先,获取时延-等效传播速度插值节点原始数据.由于试验车辆沿直线行驶,因此,需反复修正传播速度,直至逼近实际直线轨迹,记录对应的时延组与传播速度.然后,对所有节点进行插值.由于地震动信号的平均传播速度一般大于100 m/s,因此设定插值约束条件:传播速度大于100 m/s.图10为所得的时延-等效传播速度检索表等高线.可见,试验场地等效传播速度介于100~300 m/s之间,说明传播速度恒定的假设不合理.
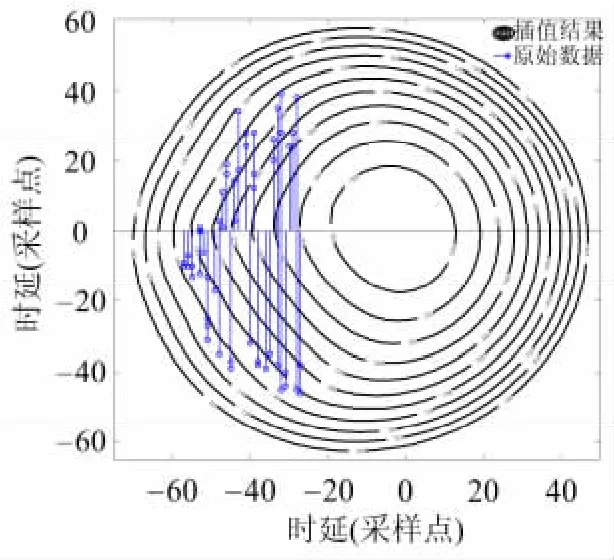
图10 试验场地的时延-等效传播速度检索表Fig.10 Search table for time delay-equivalent propagation speed at the experimental field
2.3 定位结果比较
基于固定传播速度的TDOA定位方法假设地质条件均匀,传播速度恒定,为了比较基于固定传播速度的TDOA定位方法和基于时延-等效传播速度检索表的TDOA定位方法的效果,计算了试验场地地震动信号的平均传播速度,为170 m/s,以此作为整个场地的传播速度;然后针对以二档和三档匀速运行的车辆,用2种方法分别进行定位,定位结果见图11、图12、表2和表3.可见,基于时延-等效传播速度检索表的TDOA定位方法的定位结果接近目标的真实运动轨迹,效果远优于基于固定传播速度的TDOA定位方法.

图11 二档定位结果Fig.11 Comparison of localization results for the second gear
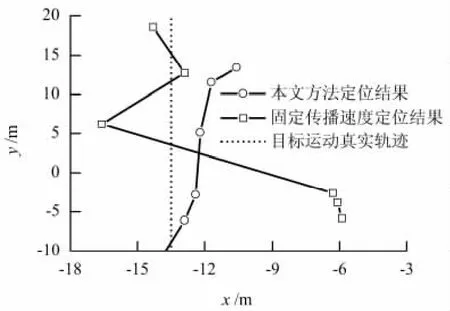
图12 三档定位结果Fig.12 Comparison of localization results for the third gear
该方法的定位效果受多方面因素影响.首先,时延误差对TDOA定位精度影响较大,要求采集的地震动信号具有较高的信噪比;其次,尽管理论上基于时延-等效传播速度检索表的TDOA定位方法可以在一定程度上补偿时延误差,然而,在实际操作中,插值精度是另一个误差来源.因此,改善硬件条件,保证信号质量,提高插值精度,可以进一步提高算法的定位精度.
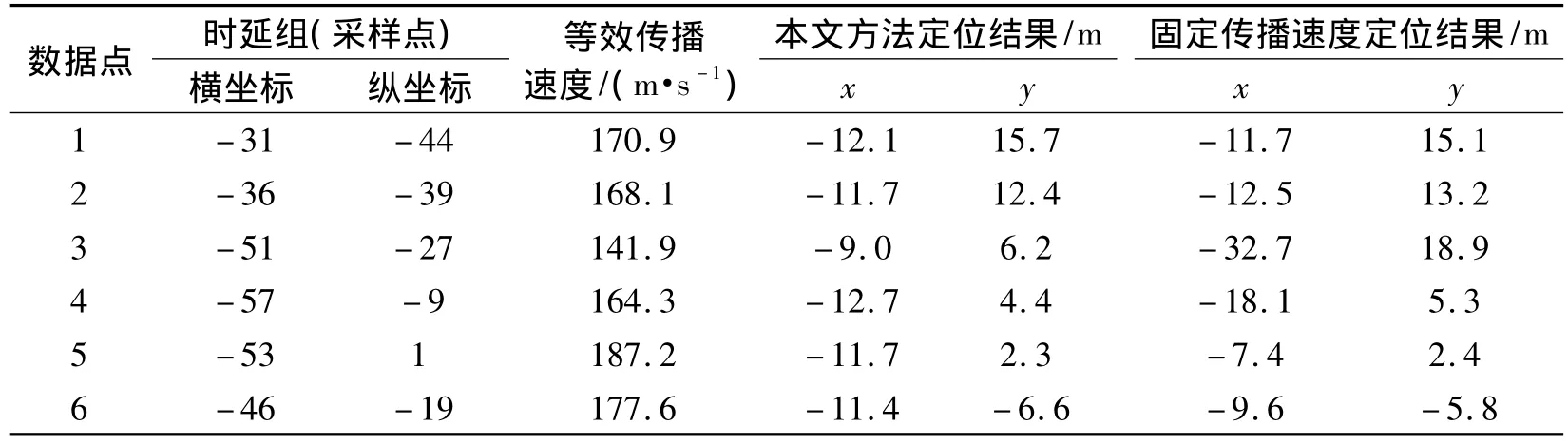
表2 二档定位参数及定位结果Tab.2 Localization parameters and results for the second gear

表3 三档定位参数及定位结果Tab.3 Localization parameters and results for the third gear
3 结论
本文通过对不均匀地质条件下地震动信号目标定位方法的研究,得到以下结论:
(1)均匀地质条件假设不符合实际;
(2)等腰直角三角形传感器阵列布置在各边延长线所夹区域存在定位盲区;
(3)五元十字阵传感器阵列布置可以消除定位盲区;
(4)基于时延-等效传播速度检索表的TDOA定位方法将位置域的传播速度转换为时延域的等效传播速度,定位效果优于基于固定传播速度的TDOA定位方法,为非均匀地质条件下地震动信号目标定位提供了一种新的思路,具有一定的工程应用价值.
[1]MCQUIDDY J H.Advanced unattended sensors and systems:state of the art and future challenges[C]∥Proceedings of Defense, Security, and Sensing.Orlando:SPIE,2010:76931J-1-76931J-10.
[2]STOTT L B,BRYSKI D D.Unattended ground sensor related technologies:an army perspective[C]∥Proceedings of AeroSense.Orlando:SPIE,2002:1-9.
[3]聂伟荣,朱继南.运动目标地震动信号的时频特征分析[J].南京理工大学学报:自然科学版,2002,26(5):478-481.
NIE Weirong,ZHU Jinan.Eigenvector analysis in time and frequency of seismic signals of moving target[J].Journal of Nanjing University of Science and Technology:Natural Science Edition,2002,26(5):478-481.
[4]焦竹青,熊伟丽,张林,等.基于曲线拟合的无线传感器网络目标定位算法[J].东南大学学报:自然科学版,2008,38(增刊 1):249-252.
JIAO Zhuqing,XIONG Weili,ZHANG Lin,et al.Target locating algorithm based on curve-fittingin wireless sensornetworks[J]. JournalofSouthwest University:Natural Science Edition,2008,38(Sup.1):249-252.
[5]SUCCI G,PRADO G,GAMPERT R,et al.Problems in seismic detection and tracking[C]∥ Proceedings of Enabling Technologies for Law Enforcement and Security.Orlando:SPIE,2001:367-376.
[6]周晖.无线传感器网络中目标定位的研究[D].上海:上海交通大学电子信息学院,2008.
[7]KNAPP C,CARTER G C.The generalized correlation method for estimation of time delay[J]. IEEE Transactions on Acoustics,Speech and Signal Processing,1976,24(4):320-327.
[8]CARTER G C.Coherence and time delay estimation[J].Proceedings of the IEEE,1987,75(2):236-255.
[9]马雯,黄建国.广义相关时延估计在被动定位系统中的应用研究[J].探测与控制学报,2000,22(3):51-54.
MA Wen, HUANG Jianguo. The application of a generalized cross correlation (GCC)time delay estimation(TDE)method in a passive localization system[J].Journal of Detection & Control,2000,22(3):51-54.
[10]孙洁娣,温江涛,靳世久.基于HHT的地面活动目标定位方法的研究[J].振动与冲击,2009,28(5):169-171.SUN Jiedi,WEN Jiangtao,JIN Shijiu.Localization principle of ground surface moving target based on HHT[J].Journal of Vibration and Shock,2009,28(5):169-171.
[11]孟令军,贾至江,严帅,等.TDOA和广义互相关相混合的无线传感器网络定位技术[J].计算机测量与控制,2011,19(7):1798-1800.
MENG Lingjun,JIA Zhijiang,YAN Shuai,et al.Location technology of mix of TDOA and generalized cross correlation[J]. Computer Measurement &Control,2011,19(7):1798-1800.
[12]李雪梅,陶然,王越.时延估计技术研究[J].雷达科学与技术,2010,8(4):362-371.
LI Xuemei,TAO Ran,WANG Yue.Summary of the time delay estimation[J]. Radar Science and Technology,2010,8(4):362-371.
[13]马晓红,陆晓燕,殷福亮.改进的互功率谱相位时延估计方法[J].电子与信息学报,2004,26(1):53-59.
MA Xiaohong,LU Xiaoyan,YIN Fuliang.Time delay estimation by using modified crosspowerspectrum phase technique[J]. Journal of Electronics &Information Technology,2004,26(1):53-59.
[14]REED C W,HUDSON R,KUNG Y.Direct joint source localization and propagation speed estimation[C]∥IEEE InternationalConference on Acoustics,Speech and Signal Processing.Phoenix:IEEE,1999:1169-1172.
[15]RICHAMN M S,DEADRICK D S,NATION R J,et al. Personnel tracking using seismic sensors[C]∥Proceedings of Aerospace/Defense Sensing,Simulation,and Controls.Orlando:SPIE,2001:14-21.
[16]ELBRING GJ, GARBINH D, LADDM D.Comparison of methods for 3D target localization from seismic and acoustic signatures[C]∥ Proceedings of AeroSense.Orlando:SPIE,2000:154-164.
[17]郑惠娜.基于无线传感器网络的地震动定位关键技术研究[D].南京:南京理工大学机械工程学院,2012.
[18]CHAN Y T,HO K C.A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

