基于斑块环境下SIS传染病模型局部稳定性分析

杨文川

（重庆师范大学数学学院，重庆 400047）

基于斑块环境下SIS传染病模型局部稳定性分析

杨文川

（重庆师范大学数学学院，重庆 400047）

首先在双线性传染率βSI和不考虑种群之间迁移问题的SIS传染病模型的基础上，改进并增加种群迁移带来的影响条件，并建立一个更加符合实际意义的SIS传染病模型；在模型满足一定条件和符合实际意义下，平衡点存在的基础上，利用基本再生数R0和特征值理论分析得出，在R0≤1时无病平衡点局部渐近稳定的充分条件；进一步利用基本再生数R0和分块矩阵理论得出，当R0＞1时地方病平衡点局部渐近稳定的充分条件；模型的建立和研究进一步丰富了传染病模型。

SIS传染病模型；无病平衡点；地方病平衡点；基本再生数

0 引 言

当今世界面临许多传染病问题，预防和控制传染病是当今世界最为棘手的问题［1］。因此建立数学模型对传染病进行分析是很有意义的研究课题。通常把总人口大致分成二部分：易感者（S）和感染者（I）。通常用模型表示［2］：

其中a表示单位时间人口迁入数量，b表示人口自然死亡率，d表示感染者通过治疗变成了易感者的变化率，其中βSI表示传染病的传然率，β是传播系数。传染率是传染病中非常重要和不可缺少的因数，关于不同传染率对传染病模型的影响问题被许多数学专家研究分析。例如，文献［3，4］中的传染率表示为文献［5］主要考虑的非线性传染率为文献［6］主要考虑这样一个非线性传染率等。考虑模型的特点，采用的非线性传染率为除了传染率对传染病的影响以外，另一个因数即种群迁移问题也是最近被大家广泛讨论的热点问题。例如，文献［2，7］主要考虑在两个斑块间的种群流动给传染病带来的影响。文献［8］中考虑了n个斑块间传染率为的SIS传染病模型。

基于以上两点建立SIS传染病模型：

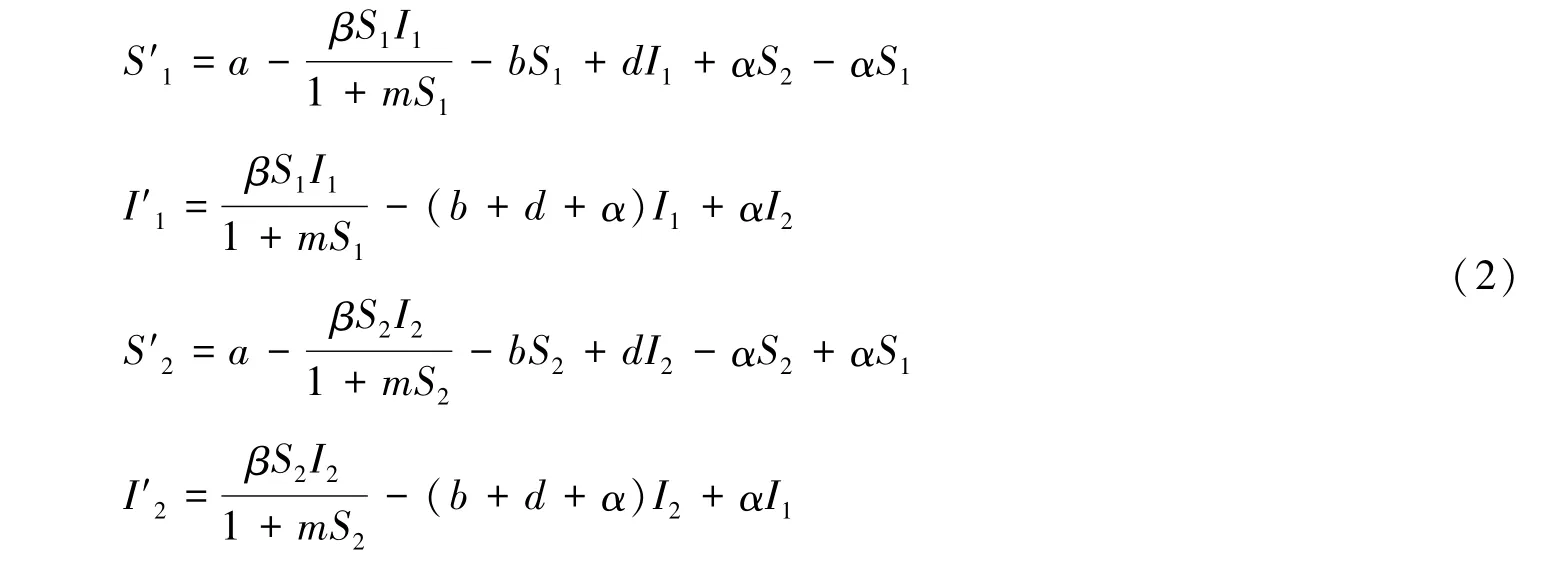
其中α表示二个斑块间的转移率，其他字母意义与式（1）相同。由实际意义出发总是假设α，β，a，b，d非负为非线性传染率［9］。

1 无病平衡点的局部稳定性

主要讨论模型（2）在无病平衡点的局部稳定的充分条件。

定理1当R0＜1时，系统（2）在无病平衡点处渐近稳定。

证系统（2）的雅可比矩阵

矩阵J（E0）对应特征方程的特征根分别为

当R0＜1时，λ1，λ2，λ3，λ4均为负根，系统（2）在无病平衡点E0处是渐近稳定的。

2 地方平衡点的局部稳定性

定理2若R0＞1时，地方病平衡点渐近稳定。

证将地方平衡点E*代入雅克比矩阵中则有

利用分块矩阵的理论，则有

而且当R0＞1时有

则迹tr（D＋B）＜0。下面讨论在R0＞1时det（D＋B）正负情况。因此，迹tr（D＋B）＜0，det（D＋B）＞0，D＋B有两个负实根。

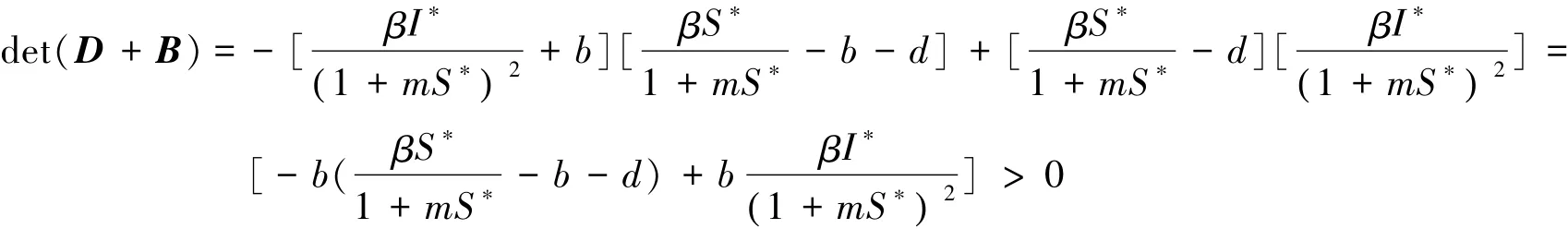
当R0＞1时

同理可证，迹tr（D－B）＜0，det（D－B）＞0。所以D－B的特征值有两个负实数根。

综上所述，在R0＞1时J（E*）的特征方程的所有特征根都是负实数，因此系统（2）在地方平衡点E*＝（S*，I*，S*，I*）处局部渐近稳定。

［1］陆征一，王稳地．生物数学前言［M］．北京：科学出版社，2008

［2］YASUHIRO T，XIAN N，JIN G．Global Dynamics of SIS Models with Transport-related［J］．Journal of Mathematical and Applications，2007（4）：1460-1471

［3］XU R，MA Z E．Global Stability of a Delayed SIR Epidemic Model with Nonlinear Incidence Rate and Time Delay［J］．Nonlinear Anal Realword Appl，2009，10（5）：3175-3189

［4］XU R，MA Z E．WANG Z P．Global Stability of a Delayed SIRS Epidemic Model with Saturation Incidence and Temporary Immunity［J］．Computers and Mathematics with Applications，2010，59（9）：3211-3221

［5］常红果．几类具有非线性传染率的传染病模型的研究［D］．陕西：陕西师范大学，2013

［6］王佳颖，窦霁虹，童姗姗．具有非线性传染率的病毒动力学模型的稳定性分析［J］．陕西科技大学学报，2011（5）：136-137

［7］李冰，王辉．一类在两个斑块内人口迁移的传染病模型的研究［J］．北京工商大学学报：自然科学版，2009，27（1）：56-60

［8］李建．n个斑块间具有路途感染的疾病传播模型［D］．重庆：西南大学，2012

［9］王倩倩，李宝麟．一类具有功能性反应的捕食者-食饵系统的定性分析［J］．重庆工商大学学报：自然科学版，2012

Local Stability Analysis on an SIS Epidemic Model in Patches Environment

YANG Wen-chuan

（College of Mathematics，Chongqing Normal University，Chongqing 400047 China）

On the basis of bilinear transmission rates βSI and SIS epidemic model in regardless of population dispersal，this paper designs a more practical SIS epidemic model by improving and adding influential condition caused by population dispersal．Meeting certain conditions with reality on the existence of equilibrium，by the basic productive number R0and eigenvalue theory this paper find that if R0＜1，the disease-free equilibrium is local and asymptotically stable，while if R0＞1，the epidemic equilibrium is local and asymptotically stable．This model proposed enriches epidemic model types further．

SIS epidemic model；disease-free equilibrium；epidemic equilibrium；basic productive number

O192

A

1672－058X（2015）03－0021－04

10．16055／j．issn．1672－058X．2015．0003．005

2014－09－10；

2014－10－21．

杨文川（1988－），男，四川商阳人，硕士研究生，从事微分动力系统研究．