证券投资基金战胜市场的能力之实证研究——基于Fama－French模拟的检验

廖海波

(宜宾学院 经济与管理学院，四川 宜宾 644007)

证券投资基金战胜市场的能力之实证研究
——基于Fama－French模拟的检验

廖海波

(宜宾学院 经济与管理学院，四川 宜宾 644007)

运用Fama－French模拟来区分运气和投资管理技能，对我国有5年以上收益率数据记录的积极管理型基金的业绩进行评价分析，结果发现:部分基金的超常业绩不能用运气解释，而应该归因于经理的技能，即有部分基金经理确实具有可以战胜市场、获得超额收益的投资管理能力。

基金;业绩;Fama－French模拟;运气

虽然证券投资基金(以下简称基金)业绩的评价方法种类繁多，但在国际主要学术刊物中，使用因子模型仍然是主流评价方法。使用因子模型评价基金业绩时，α值为正表示基金业绩超过了比较基准，获得了超额收益。国外多数研究认为，平均而言在扣除成本后积极型基金的业绩表现不如市场指数等比较基准［1］［2］［3］，但是确有一部分基金取得了超越市场的业绩表现［4］［5］。我国一些学者的研究也发现存在部分基金的业绩表现超越市场的情况［6］［7］。

那么，如果某些基金取得了超越市场的业绩表现，获得了超额收益，是由于运气好还是因为基金经理具有的投资管理技能?基金投资者能否通过选择基金经理而获得超额收益?这是事关资本市场有效性和投资者策略选择的重要问题。根据有效市场假设(EMH)理论，在达到了半强式有效的市场中，如果无内幕消息，作为专业投资者的基金经理也不能持续战胜市场，即他们获得超额收益是靠运气。Berk和 Green (2004)建立的颇有影响的理论模型则认为，基金经理的专业技能可以赚得超额收益，但是经理的技能可赚取的超额收益率会随基金规模增加而下降。如果投资者根据基金业绩推断经理的能力，偏好申购历史业绩好的基金，将导致绩优基金规模变大而收益率下降，基金投资者仍然不能获得超额收益［8］。

传统的对基金业绩持续性(persistence)进行检验的研究认为，如果过去的赢家基金(winners)的业绩能持续，则表明是由于其经理具有的技能而获得的好业绩。但是，基金业绩持续性检验在研究方法上有一个重要的缺陷，即是根据过去的短期业绩进行排名，关于赢家与输家(losers)的认定会在很大程度上受到噪声的干扰，故很难发现存在业绩持续性的证据［9］。近年来，由Kosowski等［10］、Fama和French(2010)等发展起来了一类基于bootstrap(即采用从总体中反复抽取样本的方法计算参数估计量的值，置信区间或相应统计量的值并估计这些量的分布)模拟的方法，能比较好地控制运气成分的影响。该类方法使用基金收益率的长期历史数据来计算业绩评价指标(α)，将实际业绩指标值的截面分布与bootstrap模拟所得的无超额收益情形下业绩指标值的截面分布进行比较，以进行相关推断分析。

我国基金市场的历史较短，以前未能积累足够的样本数据，故尽管在评价基金业绩时区分经理的运气和技能非常有意义，而利用前述bootstrap模拟方法来评价我国基金业绩的研究却非常罕见。本文结合我国基金市场的特点，运用Fama和French(2010)提出的模拟与统计推断方法，考察在我国有没有、有多少基金经理拥有可赚得超额收益的技能，并分析基金规模对经理技能可赚取的超额收益的影响。

一 数据与模拟方法说明

(一)数据说明

本文选择我国积极风格的开放式基金为研究对象，使用其月度收益率数据来计算基金业绩评价指标，故在由开放式基金组成的样本中剔除了指数型基金(含指数优化型)、债券型基金、货币市场基金和QDII基金，并要求进入样本的基金截至2013年12月31日至少拥有60个月的月度收益率记录。最后满足条件的基金共有212只。另将样本中在2013年12月31日净值小于15亿元的基金定义为小基金，共有66只;净值大于50亿元的基金则定义为大基金，共有54只。全部数据来源于锐思(resset)金融数据库。

(二)评价基金业绩的三因子模型

(1)式是由Fama和French(1993)提出的三因子模型［11］，被广泛运用于基金业绩评价。其中Ri，t是基金i在t月的净收益率，Rf，t为月度无风险利率。市场溢酬因子RmRft=Rm，t－Rf，t，其中Rm，t是加权平均市场收益率:由上证指数在t月的收益率(占权重0．4)、深圳成分指数在t月的收益率(占权重0．4)和中信标普国债指数在t月的收益率(占权重0．2)加权平均计算得出。之所以在计算市场溢酬因子时加入国债指数，是因为我国基金投资组合中一般都包含着债券;上述计算中所采用沪深两市和中信标普国债指数所占权重，则是国内以往研究中经常采用的经验值。规模因子SMBt和账面市值比因子HMLt的数据取自于锐思金融数据库。

使用样本基金i从2002年1月(此后设立的基金则从其有交易记录起)至2013年12月的月度收益率Ri，t的时间序列数据，应用三因子模型(1)式做普通最小二乘回归计算得到αi及其t统计量t(αi)的估计值。计算t(αi)时为减少异方差的影响，使用 Davidson和 MacKinnon (1993)提出的方法进行调整［12］。

如果αi显著为正，说明基金i的投资组合的收益经过风险调整后的业绩表现是优异的，其业绩表现超过了基准，获得了超额收益;如果αi显著为负，则说明基金i的投资组合的收益经过风险调整后表现较差，其业绩表现落后于基准。虽然SMBt和HMLt是否为风险报酬来源目前还存在着争议，但就本文的目的而言，这并无影响，SMBt和HMLt在此都可以解释为某个消极管理的投资组合的收益率，此时αi可以理解为基准调整后的收益率(benchmark adjusted return)。

(三)模拟方法

模拟的目的是描述出在无超额收益的情况下(即α为0)由于随机因素(即运气)的影响，基金α值及t(α)的分布情况。全部模拟过程采用stata12软件编程完成。

模拟用的收益率总体，由对实际收益率做如下处理后获得:对每一个实际的基金月收益率Ri，t减去实际的αi值，即模拟用月度收益率Rsi，t=Ri，t－αi。如此处理后，得到的是基准调整后零α的收益率总体，并且保持着实际收益率的特征(properties)。

抽样与计算。每次模拟，从2002年9月到2013年12月共136个月中随机地抽取一个月份A，然后使用每只基金的从2002年1月(或者从其有交易记录的月份起)至A的Rsi，t的时间序列数据，应用三因子模型(1)一只基金一只基金地回归计算相应的模拟的α值及其t统计量t(α)(弃掉其中收益率记录少于8个月的基金)。由于对所有基金都是同一个随机抽取的月份，此方法能捕捉到基金收益率中的交互相关(cross－correlation)关系以及其对t(α)估计值分布的影响［9］。模拟中有放回地重复抽样，一共进行10 000次。

由于在各次模拟中，基金月数和残差方差不同，为了控制精度的差异，在推断中将关注于α的t统计量t(α)的分布，而不是α值的分布。Kosowski等(2006)指出，当一只基金的交易记录历史短或者其拥有高风险的投资组合，这样的基金α值将呈现为虚假的突出值(outlier);而t统计量可以纠正上述虚假突出值［10］。

二 模拟结果与推断分析

使用样本基金2002年1月(或从其有交易记录起)至2013年12月的实际月度收益率时间序列数据，应用三因子模型(1)一只基金一只基金地回归计算出相应的实际t(α)的估计值，对于所得到的这个截面数据，按大小排序算出其累积分布函数(cumulative distribution function，CDF)。每一次模拟，也同样一只基金一只基金地回归计算出模拟的t(α)值，然后算出该次模拟结果的累积分布函数。通过对比以下两项进行推断:(1)使用实际收益率计算所得的，在选定的CDF的百分位(percentile)的实际t(α)的估计值;(2)10000次模拟，在同一选定的CDF的百分位的t(α)值的平均值。比如，使用实际收益率计算的t(α)在第5%百分位(5thpercentile)的值是－1．02;而模拟t(α)在第5%百分位的值，在本文的10 000次模拟中，第4 286次模拟所得值最小(－9．25)，第751次模拟所得值最大(0．25)，10 000次模拟的平均值为－1．18。由于使用的是基金的净收益率，在模拟中假设无超额收益(即设α为0)，意味着假设基金经理的技能赚取的收益刚好可弥补全部费用成本。故当实际t(α)值大于模拟值，意味着基金经理的技能赚取的收益超过了全部成本费用，获得了超额收益。

表1给出了在不同选定的百分位的情况。表1还计算了模拟值小于实际值的可能性(likelihood)——在选定的百分位，10 000次模拟中所得值小于实际值的次数所占比例——可据以进行正式推断。当大多次数的模拟值小于实际值时，就可以推断认为基金经理能赚取超过弥补各种费用成本所需的基准调整期望收益率，即具有可获得超额收益的技能;相反，如果大多次数模拟值大于实际值，则可以推断认为基金经理缺乏足够的技能来赚取可弥补成本费用的收益。

在90%百分位，98．97%的模拟值小于实际值(即10 000次模拟，有9 897次模拟的第90%百分位值小于2．76，图1为10 000次模拟的第90%百分位值的核密度函数图)。在第75%百分位，全部(100%的)模拟值小于实际值。限于篇幅而未列出的50%以上的其他各百分位的情况与上述两个百分位相似，绝大多次数的模拟t(α)值小于对应的实际值。故可以有很大把握认为，中等及以上业绩基金的经理具有可获得超额收益的技能。上述结果与国外同类控制了运气影响的研究结论相比，差别很大。Kosowski等(2006)发现美国市场中业绩最好的10%基金具有足够的选择股票的技能，能赚取超过弥补各项费用所需的收益［10］。Fama和French(2010)发现美国积极型基金很少有能获得足以弥补成本的收益，如果不考虑各种费用成本，则业绩最好的少量基金能获得超额收益［9］。

表1 实际与模拟的t(α)的累积分布函数

从表1中还可以发现，在截面分布的左尾，虽然实际的t(α)值大于模拟的平均值，但是数值比较接近，并且在第10%百分位及以下，多数次数的模拟值是大于实际值的。比如在第10%百分位，只有35．01%的模拟值小于实际值。这表明，有一小部分业绩不佳的基金的经理，其技能不足以赚取可弥补全部费用成本的收益。

图1 模拟90thpercentile值的核密度函数

表2是使用小基金和大基金两个子样本，采用与表1相同方法计算所得结果。从表2可以看出，大基金组的业绩比小基金组表现得好，在各百分位大基金组的实际t(α)值均大于小基金组。从模拟值小于实际值的可能性分析来看，在9个百分位中有8个百分位大基金组比小基金组高。所以，可以认为我国基金并未表现出随着规模增加而超额收益率下降的现象，即基金经理的投资管理技能所能赚取的超额收益率不会随基金规模递减，这与Fama和French(2010)对美国市场的研究结论一致。

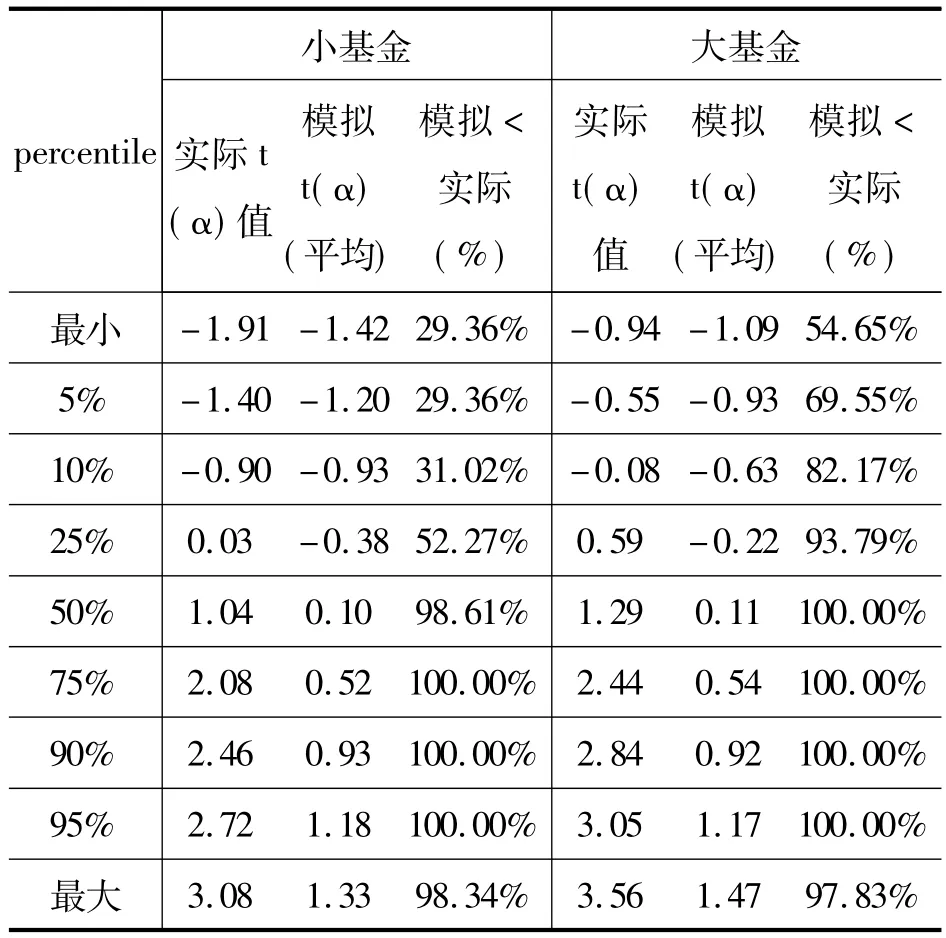
表2 小基金和大基金的实际与模拟t(α)的累积分布函数

三 结论

在控制随机因素(运气)的影响后，中等以上业绩的基金赚取了超额收益。这说明我国资本市场远未达到半强式有效，存在为数不少的(占研究样本的半数)基金的经理能凭借自己的投资管理技能赚取超额收益，这与我国资本市场投资者的结构有关，即存在大量采用积极投资策略而又缺乏投资技能的散户。在扣除交易等费用后，采用积极投资策略的投资者之间进行的是负和博弈(negative sum game)，如果部分采用积极投资策略的投资者获得了超额收益，其来源必定是部分其他采用积极投资策略的投资者的损失［13］。所以，我国股市中大量散户糟糕的投资业绩，可在相当程度上解释为什么我国有如此多的基金经理能赚取超额收益。

对大基金和小基金的对比分析还表明，基金经理的技能可赚取的超额收益率不会随着基金规模增加而下降，这对我国基金投资者选择投资策略的意义则是，如果申购历史业绩优秀的基金，可以获得超额期望收益。

［1］Gruber M J．Another puzzle:The growth of activelymanaged mutual funds［J］．The Journal of Finance，1996，51(3):783－810．

［2］Carhart M．On persistence in mutual fund performance［J］．The Journal of Finance，1997，52(1):57－82．

［3］ Cuthbertson K，D Nietzsche．False discoveries in UK mutual fund performance［J］．European Financial Management，2012，18(2):444－463．

［4］Wermers R．Mutual fund performance:An empirical decomposition into stock－picking talent，style，transaction costs，and expenses［J］．The Journal of Finance，2000，55(4):1655－1703．

［5］Petajisto A．Active share and mutual fund performance［J］．Financial Analysts Journal，2013，69(1):73－ 93．

［6］朱波，文兴易，匡荣彪．中国开放式基金经理投资行为评价研究［J］．管理世界，2010(3):172－174．

［7］屠新曙，朱梦．基金业绩评价的Fama－French三因素模型检验［J］．广东金融学院学报，2010(1):103－112．

［8］Berk JB，Richard C．Green，Mutual fund flows and performance in rationalmarkets［J］．Journal of Political E-conomy，2004，112(4):1269–1295．

［9］Fama E，K．French．Luck versus Skill in the cross section ofmutual fund returns［J］．The Journal of Finance，2010，65(5):1915－1947．

［10］Kosowski R，Allan Timmermann，Russ Wermers，ed．Canmutual fund“stars”really pick stocks?New evidence from a bootstrap analysis［J］．The Journal of Finance，2006，61(6):2551－2595．

［11］Fama E，K French．Common risk factors in the returns on stocks and bonds［J］．Journal of Financial Economics，1993，33:3－56．

［12］Davidson R，JGMacKinnon．Estimation and Inference in Econometrics［M］．New York:Oxford University Press，1993．

［13］SharpeW．The arithmetic ofactive Management［J］．Financial Analysts Journal，1991，47(1):7－9．

〔责任编辑:许 洁〕

Can M utual Funds Beat the M arket: An Analysis Based on Fama-French Simulation

LIAO Haibo
(School of Business and Economics，Yibin University，Yibin 644007，Sichuan，China)

This paper applies a new bootstrap statistical technique introduced by Fama and French to examine the performance of the Chinese open-end，domestic equitymutual fund industry with 3-factor alpha as the measure of performance．The result shows that half of the fundswhich have history ofmore than 5 years of yield data recording expected returnsmore than sufficient to cover their costs and there isevidence of superior performance(non-zero true alpha)come from manager’s skill rather than luck．

Fund;performance;Fama-French simulation;luck

F832．5

A

1671－5365(2015)03－0079－05

2015－02－04

廖海波(1974－)，男，四川开县人，讲师，博士研究生，主要从事金融投资研究。