稳态工况下水电机组主轴摆度峰峰值计算方法研究

张 飞，葛新峰，潘罗平，付 婧

（1.中国水利水电科学研究院水力机电研究所，北京 100038；2.河海大学能源与电气学院，江苏南京 210098；3.中国水利水电科学研究院信息中心，北京 100038）

稳态工况下水电机组主轴摆度峰峰值计算方法研究

张 飞1，葛新峰2，潘罗平1，付 婧3

（1.中国水利水电科学研究院水力机电研究所，北京 100038；2.河海大学能源与电气学院，江苏南京 210098；3.中国水利水电科学研究院信息中心，北京 100038）

对目前状态监测与现场试验中主轴摆度峰峰值计算的常用方法进行了综述，将计算方法分成两类：极值法和置信度法。通过实例分析指出稳态工况下极值法计算时存在结果不稳定，且结果依赖于滤波器选择的问题。研究采用置信度法计算峰峰值，实例分析表明置信度法结果优于极值法。在95%的置信度下，当计算周期数不小于6时，采用95%置信度法对原始数据及不同滤波器作用下的数据计算得到的峰峰值结果均收敛，置信度法下的峰峰值计算结果相容。

水电机组；主轴摆度；峰峰值；极值法；置信度法

水轮发电机组主轴摆度监测综合反应了机组的运行状态信息，是水电机组状态监测中重要内容［1－2］。通常采用涡流位移传感器监测主轴摆度峰峰值的方法，对机组运行稳定性情况进行分析。长期以来，峰峰值计算存在3种不同的方法：时段法、平均时段法以及置信度法［3］。然而这3种方法之间是否存在差异，以及如果存在差异，差异之间是否显著，并没有相关研究结论。近年来随着三峡、向家坝、溪洛渡电站等大容量机组的启动调试及运行，通常有若干（中国水利水电科学研究院、四川调试所、长电技术中心、华科同安TN8000机组在线监测系统等）振摆监测机构对机组主轴摆度进行测试，由于采用不同的算法，经常导致测试结果存在差异，甚至冲突，从而影响机组启动调试、竣工验收及日常运行等相关工作。进而导致对峰峰值计算方法的严重关切。基于此，本文以稳态工况下某机组主轴摆度信号为研究对象，考虑了不同滤波器的作用，对峰峰值的3种计算方法进行了研究，利用实例对不同算法进行验证，指出了不同算法间的差异，并给出了主轴摆度峰峰值的推荐算法。该计算方法对水电机组振动及压力脉动峰峰值计算方法也具有参考意义。

1 摆度与峰峰值的定义

在GB／T28570－2012［4］第3.4节中定义主轴摆度为：水轮发电机组主轴某部位相对于该部位邻近固定部件的径向振动，又称轴相对振动。

在文献［3］第3.2.1.12节中定义峰峰值为：一个量的最大值和最小值的代数差，正弦量的峰峰值为振幅的两倍。

在文献［5－6］中给出了以峰峰值作为评价依据的运行区范围划分，在附录中示意给出了理想情况下的峰峰值计算方式：摆度波形最大值与最小值的差值。

根据上述关于主轴摆度和峰峰值的定义得到主轴摆度峰峰值定义为：主轴摆度信号中最大值与最小值的代数差。令一段时间内无噪声的主轴摆度信号连续采样获得的样本值为：

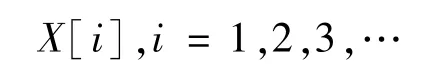
主轴摆度摆度峰峰值定义为：

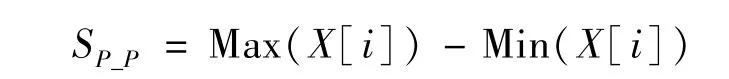
一个理想无噪声摆度信号的摆度信号峰峰值见图1所示。该信号由一倍频和两倍频信号分量组成。

理想情况下，如机组处于稳态运行工况，此时水头和功率保持恒定，主轴摆度峰峰值应具有不依赖于计算方法的唯一值。现实的情况是：机组在稳态运行过程中，一是由数据采集系统获得的信号不可避免受到噪声干扰，导致峰峰值计算存在明显波动；二是机组旋转过程中也难免受到来自于电气、水力以及机械方面的随机扰动，因此主轴摆度峰峰值并非是恒定数值，而是具有较为稳定的统计分布规律［7］。为探明不同主轴摆度峰峰值算法间的差异，下文将首先对峰峰值的不同算法进行讨论，然后以实例对峰峰值的计算结果进行分析。

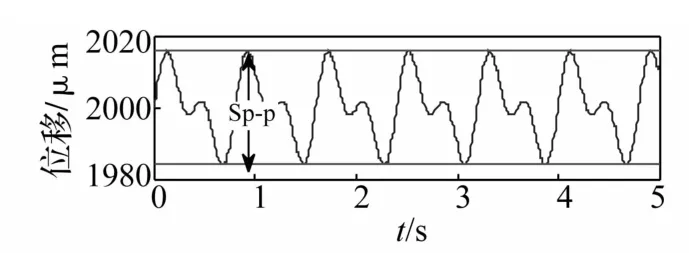
图1 峰峰值概念定义示意Fig.1Connectional definition of peak-to-peak value

图2 典型的置信度法峰峰值计算Fig.2 A typical peak-to-peak value calculation with confidence level

图3 图2所示数据的分布Fig.3 Data distribution corresponding to Fig.1

2 峰峰值计算方法

目前峰峰值计算主要参照文献［3］中第10.2.1节关于压力脉动的峰峰值算法进行计算，标准中规定了3种计算峰峰值的方法：时段法、平均时段法和置信度法。具体定义见规范。

时段法和平均时段法基本属于同一种方法。平均时段法是时段法的多个计算结果取平均从而获得一个峰峰值，时段法侧重于获得峰峰值随时间变化的趋势。这两种方法中也隐含着另一种方法：滑动窗口时长计算方法，即每次计算数据的时段长度是固定的，每次向前滑动固定时间窗口。由于目前有些状态监测厂家采用了基同步整周期采样技术［8］，因此对于时段的选取是基于旋转周期计算的。尽管时段法和平均时段法计算过程略有差异，但均是计算最大值与最小值的差值，本文统称为极值法。

采用时段法和平均时段法计算中，一个重要参数是时段的选取。通常涡流位移传感器的标称低频响应最低可以达到0.1 Hz，大量的现场试验研究表明，机组稳定性参数主要受电磁、机械和水力方面的影响，其中电磁方面影响主要是极频，机械影响主要在转频及其倍频，水力方面除转频及其倍频外还存在分数阶频率成分，如部分负荷区的尾水管压力脉动频率为1／3倍～1／4倍转频［9］。因此为了合理计算主轴摆度峰峰值，每个计算时段应至少包含尾水管低频脉动周期。因此规范中给出要求是每个时段中至少包含一个尖锐峰值。这导致在实用计算时，各个厂家选取计算周期具有很大的随意性。但是周期的选取并非越长越好，本文将给出基于试验的实测数据分析结果。

置信度法中，采用的算法是基于97%或95%置信度数据区间的计算方式［3］。置信度即置信区间，根据文献［10］中第1.28款的定义：参数θ的区间估计（T0，T1），其作为区间限的统计量T0，T1，满足P［T0＜θ＜T1］≥1－α。稳态工况下，根据这一定义得到的摆度峰峰值是一个区间，该区间表明在一定的置信水平下，峰峰值的一个可信范围。而在实用计算中，采用置信度法过程是将主轴摆度进行分区，然后剔除不可信的区域后计算区间范围，典型的计算过程为：

（1）获得一定时间内的摆度信号，点数为N；

（2）对摆度信号采样点数值进行排序；

（3）索引第0.5αN和（1－0.5α）N的值（如果索引计算非整数，则就近取整），并计算绝对差值，该值为置信度α下的峰峰值。

一个典型实例见图2和图3所示。图2为稳态工况下的某机组下导轴承位置处的摆度波形，共25个周期。图3给出了采样信号的分布（概率密度）。采用极值法计算25个周期的峰峰值为156.92μm，而采用97%置信度方法计算得到的峰峰值为128.03μm，95%置信度的峰峰值为120.97μm（图2和图3中横线对应数值的差值）。由计算结果可知，采用极值法和置信度法得到的计算结果存在明显差异。

采用置信度法计算时，考虑极端情况下对一个正弦波进行取样，按上述过程计算某一置信度下的峰峰值会导致波形峰谷被消除的情况，从而导致峰峰值比实际值小，但是这种减小的幅度是可控的，依赖于合理的置信度的选择。出现这种原因是因为在计算时所剔除的数据并非不可信数据。对主轴摆度而言，通常具有明显的主频，是周期性变化量。本质是传感器测量平面上的轴心轨迹在相应传感器上的投影距离［5－6］，即：指定方向的电涡流位移传感器对某一方向的连续距离进行测量，轴心在这个方向做往复运动，运动轨迹的投影即该传感器的测量值。这一往复运动受机械、电磁以及水力条件的约束［8］。理论上，恒定的约束产生恒定的轨迹，因此稳态工况下轴心轨迹的形状保持较为稳定的形状［11］。但因机械、电磁和水力约束条件受随机扰动的影响，这一影响可以是水力脉动、负荷随机变化等，轴心轨迹必然存在一定程度的不确定性。不确定性造成的影响是：虽然轴心轨迹的形状保持恒定，但是某一瞬时（这可以理解为对于每一旋转周期，轴表面某个点在传感器测试方向上的位移）轨迹具有不确定性。根据置信度的定义，对每一次轴位移峰峰值计算结果而言，这是一次单一测量，在稳态工况下对大量峰峰值的分布规律服从正态分布［7］（这种分布规律不依赖于计算方法的选择）。在上述计算步骤中，假设的前提是每个采样点，即一次位移结果，为一次观测。置信度法计算步骤的含义是获得众多观测点的分布，而后取1－α的全部数据，计算其上下限，见图3。

综合本节分析，主轴摆度峰峰值计算存在两种方法：极值法和置信度法。

3 实例分析

某电站机组转速187.5 RPM，对机组稳定工况下的下导轴承处摆度进行连续同步整周期采样。本文采用其中3个小时的数据，共计33 750个周期。为探明不同周期数、不同滤波方法（基于目前的状态监测与趋势分析系统中大都对数据进行了滤波处理）及不同计算方法对峰峰值的影响，分别采用如下分析过程进行数据分析：

（1）利用不同的滤波器对原始数据进行滤波：五点三次平滑滤波、巴特沃斯二阶滤波器滤波（截止频率为100 Hz）、自适应EMD平滑滤波三种滤波方法；

（2）对不同滤波器作用后的数据，以滑动窗口方式（窗口时长为2、3、4…29个周期，滑动步长为一个旋转周期），分别采用极值法和95%置信度法（对应±1.96倍标准差）计算主轴摆度峰峰值，并计算全部峰峰值的均值及标准差。

3.1 极值法计算峰峰值

采用极值法计算得到的峰峰值均值随计算周期的变化情况见图4所示。由图4可见：当采用不同的计算周期数时，峰峰值随着计算周期的延长而增大，且不依赖于是否采用滤波器以及何种滤波器。这是因为极值法计算在理论上对于稳定无噪声干扰有解析表达式的波形是非常严格的。然而对于实际轴摆度监测数据，由于采样信号受到噪声以及来自于水力、机械和电气随机因素的干扰，即使在稳定工况下，波形似乎不是高度的“稳定”，典型的波形如图2所示。由于周期数的增大，参与计算的采样点数不断增加，一方面受信号噪声及机组水力、负荷等随机扰动的影响，最大值随数据点数的增多不断增大，最小值随数据点的增多不断减小，从而导致最大值与最小值的代数差值发散，这可以理解为随着参与计算点数的增多，图3所示的概率密度函数两端不断外扩；另一方面，随着参与计算点数的增多，某一极值，出现的次数也增多。这也解释了为什么不同的调试厂家给出的峰峰值由于计算周期的不一致以及滤波方法的不统一而使得结果存在差异。有时这种差异是不可忽视的。

图4 极值法峰峰值计算结果（均值趋势）Fig.4 Mean value trend of peak-to-peak value calculated by extremum method

图5 极值法峰峰值计算结果（标准差趋势）Fig.5 Standard deviation trend of peak-to-peak value calculated by extremum method

图6 95%置信度法峰峰值计算结果（均值趋势）Fig.6 Mean value trend of peak-to-peak value calculated by 95%confidence levelmethod

图5给出了原始数据及采用不同滤波器作用后的标准差收敛情况。由图5可见：如果不采用滤波器，采用极值法对原始数据计算峰峰值，峰峰值的标准差不稳定，有发散的可能，因此有必要对原始数据进行消噪或滤波处理。而采用滤波器后，虽然峰峰值没有收敛，但峰峰值的标准差不依赖于滤波器的选择，具有一致的收敛规律，表明随着计算周期数的增大，虽然峰峰值有增大的趋势（受限于轴瓦间隙的调整，峰峰值不能大于两侧的间隙和），但标准差逐渐减小。因此滤波器有减小峰峰值计算结果离散化的作用，在采用极值法计算峰峰值时应对采样信号进行适当的滤波处理，以减小计算结果的离散性。

综合3.1节说明稳态工况下采用极值法计算峰峰值时：一是由于直接采用原始数据计算峰峰值随着计算周期的延长，峰峰值及其标准差不收敛，不能直接对原始数据进行峰峰值计算；二是由于峰峰值随着计算周期数的增大有增大的趋势，因此不同的周期数计算的结果具有较大偏差，采用极值法时有必要采用统一的计算周期数，否则将会造成由于所用周期数的不同导致计算结果不具有可比性。

3.2 95%置信度法计算峰峰值

采用95%置信度法计算峰峰值时，根据前文的分析，这意味着对原始采样点进行统计分区，计算上下分位点的代数差值，从而获得峰峰值。分别对下导摆度原始数据以及不同滤波器作用下的数据进行峰峰值计算，结果见图6和图7所示。

由图6可见，峰峰值的均值随着计算周期的延长而逐渐增大并最终趋于收敛，同时是否滤波以及采用何种滤波器并不影响计算结果收敛性。这表明采用95%置信度法较极值法具有优势。为合理判断计算周期数对收敛情况的影响，令N个周期计算的峰峰值为SPP＿N，N+1个周期计算的峰峰值为SPP＿N+1，以相邻两个周期数的峰峰值相对误差为收敛依据，见下式：

采用式（1），针对案例数据计算结果见图8所示。

计算结果表明：不同滤波器作用下的数据，当采用95%置信度法获得主轴摆度峰峰值时收敛性高度一致，且当计算周期数为6时误差已小于0.1%，计算结果收敛性不依赖于数据是否滤波及滤波方法的选择。

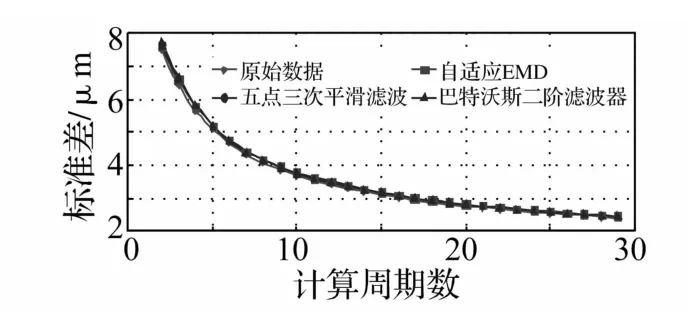
图7 95%置信度法峰峰值计算结果（标准差趋势）Fig.7 Standard deviation trend of peak-to-peak value calculated by 95%confidence levelmethod

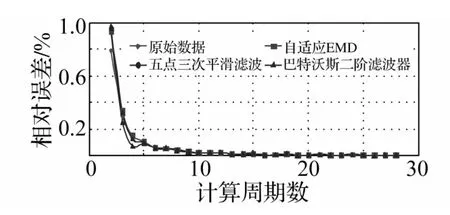
图8 95%置信度峰峰值计算收敛趋势Fig.8 Mean value convergence of peak-to-peak value calculated by 95%confidence levelmethod

图9 95%置信度峰峰值计算收敛趋势Fig.9 Mean value convergence of peak-to-peak value calculated by 95%confidence levelmethod

由图6中可以看到另一方面，由于采用不同的滤波器，数据进行了不同程度的修正，因此不同滤波器作用下得到的稳态值峰峰值的均值存在差异。当计算周期数大于等于6以后，在不同的计算周期数下，均以原始数据计算得到的峰峰值为基准，自适应EMD滤波、五点三次平滑滤波和巴特沃斯二阶滤波器滤波后的计算结果误差值分别为－0.78%、－1.28%和－1.85%。考虑到收敛之后标准差的值位于2～3μm之间，同时考虑到95%置信度区对应的数据精确度为±1.96倍的标准差，以原始未滤波数据得到的峰峰值为基准，滤波后计算得到的峰峰值的标准差为±3.66%，因此3种滤波器下的结果是相容的。即：在95%置信度下，采用95%置信度法对不同滤波器得到数据进行峰峰值计算，其结果与相同计算方法通过原始数据直接计算得到的峰峰值结果具有一致性。

根据以上分析可以得出：稳态工况下，采用95%置信度峰峰值计算时，应不少于采用6个周期的数据。考虑到当周期超过6以后，计算结果误差小于0.1%，因此采用6个周期是合理的。另外，当周期数大于等于6时，由于在95%置信度下，采用滤波后的数据与直接采用原始数据计算峰峰值结果相容，没有明显差异，因此推荐直接采用95%置信度法对原始数据计算峰峰值。这一规律也可以从令一方面得到解释：在某一稳定工况下，数据的分布规律保持不变，即信号的概率密度不变，随着计算周期数的增大，由于数据分布规律并不改变，计算周期数增大只是在一定程度上增大了计算使用的数据点数；然而计算周期数存在一个下限，在0.1%的误差要求为6个周期，如果周期数太少，计算结果并不能保证使用的数据是一个完整的数据分布，即采样样本不能代表整体数据。

为了验证该结论的有效性，研究人员对另一台机组上导轴承位置处的摆度数据采用95%置信度法进行了峰峰值计算，收敛结果见图9所示。从图9可见，对其它不同类型机组不同测点的摆度数据进行研究，结果具有一致性。

4 结 论

本文采用统计手段对水电机组稳态工况下的主轴摆度峰峰值计算方法进行了分析，得到以下两点启示：

（1）采用ISO7919.1－1996或GB／T11348.1－1999计算出的峰峰值随着计算周期的延长结果趋于离散，该离散性不依赖于原始数据是否滤波以及滤波器的种类；相同计算周期时，采用不同的滤波手段对原始数据进行计算，得到的峰峰值有较为明显的差异；如果采用该方法对摆度峰峰值进行评价，应指定计算周期数和滤波方法。鉴于周期数和滤波方法的随意性，不推荐采用该方法计算主轴摆度峰峰值。

（2）采用95%置信度法计算峰峰值时，随着计算周期的延长，结果收敛，且该收敛不依赖于原始数据是否滤波及滤波器的种类；对原始数据及滤波器作用下的数据进行不同周期数的峰峰值计算，结果表明当计算周期大于等于6时，峰峰值误差小于0.1%，因此计算周期数应不小于6；当采用95%置信度方法计算主轴摆度峰峰值时，不同滤波器下得到的峰峰值与通过原始数据直接计算得到的峰峰值在95%置信度下相容，没有明显的差异。

综合以上两点启示，建议稳态工况下水电机组主轴摆度监测计算峰峰值时对机组摆度采用同步整周期采样，采样长度不少于6个旋转周期，同时利用95%置信度法直接对原始数据计算峰峰值。

［1］朱传古，田桂岩，杨克，等.水电厂主设备分析诊断策略［J］.水电自动化与大坝监测，2012，36（5）：5－9.

ZHU Chuan-gu，TIAN Gui-yan，YANG Ke，et al.An analysis and diagnosis strategy for main equipment of hydropower plant［J］.Hydropower Automation and Dam Monitoring，2012，36（5）：5－9.

［2］刘晓亭，冯辅周.水电机组运行设备监测诊断技术及应用［M］.1版.北京：中国水利水电出版社，2010.

［3］GB／T 17189－2007.水力机械（水轮机、蓄能泵和水泵水轮机）振动和脉动现场测试规程［S］.北京：中国标准出版社，2008.

［4］GB／T28570－2012.水轮发电机组状态在线监测系统技术导则［S］.北京：中国标准出版社，2012.

［5］GB／T 11348.1－1999.旋转机械转轴径向振动的测量和评定第1部分：总则［S］.北京：中国标准出版社，1999.

［6］ISO 7919.1－1996.Mechanical vibration ofnon-reciprocating machines—Measurements on rotating shafts and evaluation criteria—Part 1：General guidelines［S］.2nd ed.International standard organization，1996.

［7］张飞，潘罗平，安学利.水轮发电机组稳定性参数统计特性与监测报警阈值研究［J］.水力发电学报，2013：32（5）：269－272.

ZHANG Fei，PAN Luo-ping，AN Xue-li.Study on statistical characteristics and maintenance alarm strategy for stability parameters of hydraulic turbine generator unit［J］.Journal of Hydro-Electric Engineering，2013，32（5）：269－272.

［8］朱浩，陈喜阳，李友平，等.水电机组在线监测中同步整周期采样实现策略［J］.电力系统自动化，2007，31（4）：80－84.

ZHU Hao，CHEN Xi-yang，LIYou-ping，et al.Application of synchronouswhole-periodic sampling in the hydropower onlinemonitoring system［J］.Power System Automation，2007：31（4）：80－84.

［9］马震岳，董毓新.水电站机组及厂房振动的研究与治理［M］.北京：中国水利水电出版社，2004.

［10］GBT 3358.1－2009.统计学词汇及符号第1部分一般统计术语与用于概率的术语［M］.北京：中国标准出版社，2010.

［11］翁桂荣，薛峰.几种特征描述方法在轴心轨迹识别中的应用［J］.振动、测试与诊断，2007，27（4）：295－299.

WENG Gui-rong，XUE Feng.Characteristic method applicationin shaft orbit identification［J］.Journal of Vibration，Measurement＆Diagnosis，2007，27（4）：295 －299.

Shaft run-out's peak-to-peak value calculation method for
a hydraulic power unit under stable conditions

ZHANG Fei1，GE Xin-feng2，PAN Luo-ping1，FU Jing3
（1.Department of Hydro－Electrical Engineering，China Institute ofWater resources and Hydropower Research，Beijing 100038，China；2.College of Energy and Electrical Engineering，Hohai University，Nanjing 210098，China；3.Department of Information Technique Service，China Institute ofWater resources and Hydropower Research，Beijing 100038，China）

Review on the shaft run-out calculationmethods for hydralulic power unitswere performed.Under stable working conditions，the calculation methods could be classified into the extremum method and the confidence level one.Case studies indicated that the peak-to-peak values calculated with the extremum method are not stable，and the results depend on the filter selections.The peak-to-peak value calculation with the 95%confidence levelmethod was done.Case studies showed thatunder the 95%confidence level，when the calculation period is greater than 6 or equal to 6，the peakto-peak values calculated with the 95%confidence levelmethod all converge，and all convergences do not depend on if the data are filtered or filter types；four series of peak-to-peak values are compatible.

hydraulic power unit；shaft run-out；peak-to-peak value；extremum method；confidence levelmethod

TH113.2；TK730.7

A

10.13465／j.cnki.jvs.2015.21.029

国家自然科学基金资助项目（51139007，51309258）；江苏省博士后基金资助项目（1102072c）

2014－06－09 修改稿收到日期：2014－11－11

张飞男，硕士，高级工程师，1983年2月生

潘罗平男，博士，教授级高级工程师，1969年5月生