连接Maxwell模型的两相邻结构地震易损性分析
吴巧云,朱宏平,陈楚龙
(1.武汉工程大学资源与土木工程学院,武汉 430073;2.华中科技大学土木工程与力学学院,武汉 430074)
连接Maxwell模型的两相邻结构地震易损性分析
吴巧云1,2,朱宏平2,陈楚龙2
(1.武汉工程大学资源与土木工程学院,武汉 430073;2.华中科技大学土木工程与力学学院,武汉 430074)
对连接Maxwell模型的两相邻钢筋混凝土框架结构建立二维模型,考虑了梁柱单元及阻尼器单元在大震作用下的非线性行为,通过大量的增量动力分析(IDA),研究了Maxwell阻尼器优化参数理论表达式在结构经历初始弹性、屈服直至倒塌全过程的适用性,并基于IDA分析的结果,对结构未控和控制情况下的地震易损性曲线进行了比较分析,从性能评估的角度研究了Maxwell阻尼器对相邻结构在不同地震波及不同地震动强度水平下的控制效果。通过相邻结构在不同地震动强度水平下的顶层位移时程发现,Maxwell阻尼器在小震作用下对两结构顶层位移控制效果均较好,但是在大震作用下,仅对结构2有明显的控制效果;由控制和未控时的相邻结构的地震易损性曲线亦可看出,Maxwell阻尼器对结构2在各性能水平下的控制效果均优于结构1。最后,通过大量的参数化分析,基于相邻结构地震易损性最小原则提出了合适的阻尼器参数值。
相邻结构;地震易损性;Maxwell阻尼器;增量动力分析;性能水平
自1985年墨西哥城市大地震后,相邻结构在地震作用下的碰撞问题得到了国内外学者的广泛关注。许多学者提出了在相邻结构之间安装控制装置的思想,利用相邻结构之间的相对振动来消耗或吸收部分能量,以达到减振的效果。朱宏平等[1]提出了一种利用主从结构间的相互作用来减小地震响应的控制方法,推导了在平稳白噪声激励下被动耗能单元的优化刚度和优化阻尼的一般表达式,并分析了不同结构参数对控制效果的影响;随后朱宏平等[2]将相邻结构简化为两单自由度体系,用Voigt黏弹性阻尼模型表示被动连接单元,运用Kuhn-Tucker优化原理导出了在地面随机激励下被动连接单元的优化刚度和阻尼值的一般表达式;此后,朱宏平等[3-7]又基于能量统计原理分别推导了双体单自由度体系间Kelvin型和Maxwell型阻尼器优化参数的解析表达式。Zhu等[8-9]采用在双体单自由度结构间设立Kelvin型、Maxwell型被动控制单元的优化参数表达式,并基于等效双体单自由度体系求得了相邻多层剪切型结构间控制装置的最优参数。通过数值分析证实了采用等效双体单自由度体系代替相邻多自由度结构体系的正确性和有效性。Xu等[10]求得了连接LQG控制器的两相邻结构的地震响应的封闭解,通过此封闭解可以进行相邻多自由度结构间的参数化研究,并可找到控制和减小相邻结构间最大响应的有利参数。Bhaskararao等[11-12]采用摩擦阻尼器连接两相邻结构,研究了在地震作用下的控制效果,结果表明,采用摩擦阻尼器也可以获得良好的耗能减震效果。Bhaskararao等[13]将基底加速度模拟成简谐振动和平稳高斯白噪声随机激励,对连接黏滞阻尼器的两相邻单自由度体系的动力响应进行了研究。推导了结构的运动方程并求出了相邻结构的相对位移和绝对加速度响应。结果表明当黏滞阻尼器具有合适的阻尼时可以减小相邻结构间的响应。Basili等[14-15]进行了连接非线性滞回装置的相邻结构的被动控制优化研究。通过将相邻结构简化为单自由度体系,基于随机等效线性化方法求出了高斯白噪声和过滤白噪声激励下滞回装置的优化参数。Ok等[16]基于多目标遗传算法和随机等效线性化方法对连接滞回阻尼器的相邻结构进行了优化控制研究。通过大量的非线性随机振动分析研究了考虑地震动随机性的优化设计的鲁棒性。
综上所述,虽然在相邻结构的振动控制方面有一定的研究,但是目前取得的成果非常有限,仍存在一些问题需要继续研究:以往相邻结构的振动控制研究未曾对相邻结构在不同发生概率、不同强度地震作用下的抗震性能及地震易损性进行研究,以满足结构安全及使用功能的多级抗震设防目标。然而近年来的几次大地震,使人们意识到地震所带来的不仅仅是巨大的经济损失,更会带来严重的社会影响[17-20],这就使得社会和业主对建筑抗震性能有多层次的要求:设计的建筑结构在强震作用下不仅能够抵御碰撞和倒塌,而且还要能够保证结构物的使用功能在地震作用下不致丧失,实现结构物多级抗震设防目标,即需要引进基于性能的多目标抗震设防的性能设计的概念。因此,作为地震多发国家,在我国开展基于性能的相邻结构的振动控制研究具有重要的理论研究意义和工程应用价值。
本文对连接Maxwell模型的相邻钢筋混凝土框架结构进行了增量动力分析,基于增量动力分析的结果进行后处理编程,得到了控制和未控时相邻结构的地震易损性曲线。从性能评估的角度研究了阻尼器优化参数理论表达式在不同地震波及不同地震动强度下控制性能的有效性,并基于地震易损性最小原则得到了合适的阻尼器参数。
1 控制单元优化参数及地震记录的选取
1.1 控制单元优化参数
初步选择Maxwell型被动控制单元的优化参数为与相邻结构总质量和第一阶模态频率比有关的计算参数,控制目标为使结构1和结构2的总振动能量最小。设μ=m1/m2为结构1和结构2的质量比,β=ω2/ω1为结构2和结构1的自振频率比,并限制β≤1,对于频率比β>1的情形只需将结构1与结构2角色互换即可,则Maxwell型黏滞流体阻尼器总的优化参数ξopt与χopt表达式为[4]:
当μ≥1时:
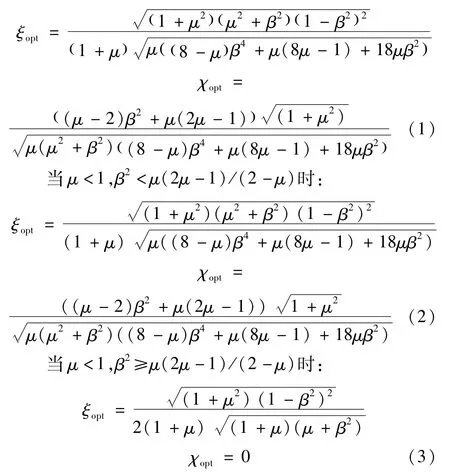
Maxwell型黏滞流体阻尼器的零频率阻尼系数与松弛时间可表示为:
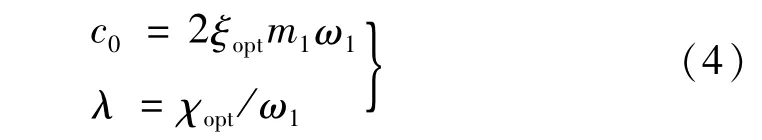
1.2 地震记录的选取
有关学者曾研究过,对于中等高度的建筑,选取10~20条地震记录进行增量动力分析可以得到较为精确的地震需求估计[21]。参见文献[22]的地震动选取原则,算例所处场地为《建筑抗震设计规范》(GB5011 -2010)中所规定的二类场地,故通过美国太平洋地震研究中心的数据库,本文选取相当于Ⅱ类场地的20条震级在6.5~6.9的实际远场地震记录作为对比分析,各地震记录的详细信息参见文献[23]。
2 相邻结构计算模型
本文分析采取模型为西安某高校行政办公楼,为两相邻结构,结构1为10层钢筋混凝土框架,结构2为6层钢筋混凝土框架,结构平立面布置均匀,为简化计算,两结构各取其中一榀建立二维模型。相邻结构计算模型如图1所示。两结构主要设计参数如下:建筑场地Ⅱ类,抗震设防烈度8度,设计基本地震加速度0.20 g,设计地震分组第二组,框架抗震等级结构1为一级,结构2为二级[24]。基本风压0.35 kN/m2,基本雪压0.25 kN/m2。混凝土强度等级柱、梁、楼板均为C35;梁、柱主筋HRB335级,箍筋HPB300级;结构层高均为3.6 m。截面尺寸:结构1:梁300 mm×800 mm;柱750 mm×750 mm;结构2:梁300 mm×800 mm;柱800 mm×800 mm。各结构楼板厚100 mm。
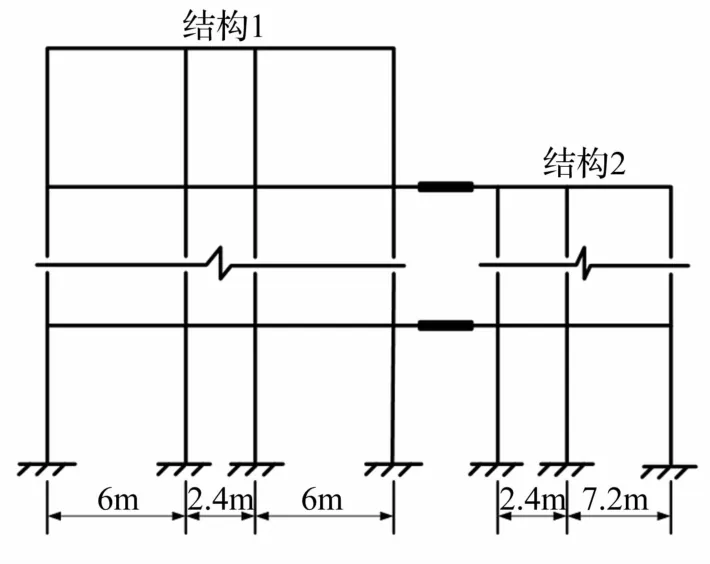
图1 相邻结构计算模型Fig.1 Calculation model of adjacent structures
采用OpenSees程序对该结构建立二维模型并进行增量动力分析(Incremental Dynamic Analysis,IDA)。Maxwell阻尼器材料选用uniaxialMaterial Maxwell模拟。梁、柱及Maxwell阻尼器选用基于位移的非线性纤维梁柱单元模拟。采用OpenSees分析得到结构1的第一阶自振频率ω1=8.418 rad/s,结构2第一阶自振频率ω1=17.525 4 rad/s。结构1总质量为303.070 5 t,结构2总质量为203.802 1 t。
采用Maxwell阻尼器,结构每层各布置一个阻尼器(共计6个),阻尼器参数:若使结构1和结构2的总振动能量最小,由式(1)~(4)计算出的阻尼器阻尼系数和为c0=1.447 8×106N·s/m,松弛系数为0.040 8,刚度系数和为k=3.548 5×106N/m,则每个阻尼器阻尼系数、刚度系数分别为2.413×105N·s/m、5.914× 106N/m。
3 算例分析
3.1 结构性能水平的确定
选取可以表征结构整体破坏指标的最大层间位移角作为工程需求参数(Damage Measure,DM),将结构的极限状态划分为立即使用(Immediately Occupation,IO)、轻微破坏(Slightly Damage,SD)、生命安全(Life Safety,LS)和防止倒塌(Collapse Prevention,CP)四个状态,各极限状态对应的性能目标见表1[25]。

表1 各性能极限状态的性能目标Tab.1 Lim its of each performance lim it state
3.2 增量动力分析
选取峰值加速度为地震动强度指标(Intensity Measure,IM),选取最大层间位移角为工程需求参数指标(DM),对相邻结构进行前述20条地震动作用下的增量动力分析(IDA),每条地震动调幅25次,得到结构1、结构2未控和受控时的IDA曲线如图2、图3所示。
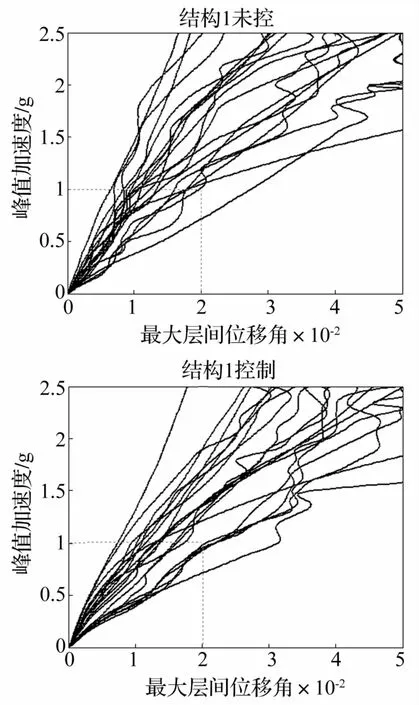
图2 结构1IDA曲线Fig.2 IDA curves of structure 1
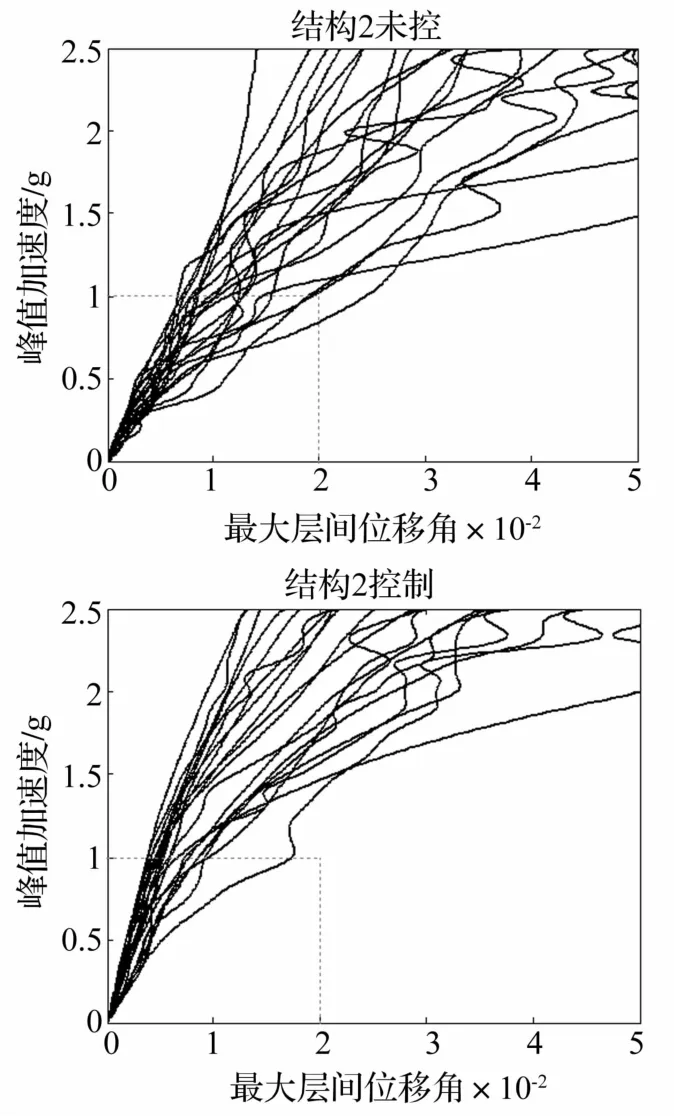
图3 结构2IDA曲线Fig.3 IDA curves of structure 2
由图2结构1未控和控制下的IDA曲线可以看出,相同的地震动水平下结构1在未控和控制下的最大层间位移角的响应值差别并不大,即由IDA曲线并不能发现Maxwell阻尼器对结构1有较好的控制效果;而由图3结构2的IDA曲线可以较为清楚的发现在各地震动水平下,受控情况下的最大层间位移角均小于未控情况下的响应值,因此,由此可以看出Maxwell阻尼器对结构2在各地震动及地震动强度水平下均有较好的控制效果。
为了更为清楚的比较相邻结构在Maxwell阻尼器控制下、在不同地震动强度水平下对结构1和结构2的控制效果,图4、图5给出了相邻结构在Imperial Valley(015分量)地震波作用下,峰值加速度为0.2 g、0.9 g时各结构顶层位移时程响应情况。由于篇幅受限,其余19条地震波作用下的顶层时程响应从略。
由图4可以看出,当地震动强度较小时,结构处于弹性阶段,按照弹性理论计算的连接相邻结构的Maxwell阻尼器优化参数对两结构的控制效果均较好;但是,在大震作用下,两结构表现出较强的非线性行为,由图5可以看出,Maxwell阻尼器仅对结构2的控制效果较好,对结构1的控制效果不明显,甚至在某些时刻会略放大结构1的响应。因此按照文献[4]设计的Maxwell阻尼器,当结构遭遇大震时尚应重新考虑阻尼器的优化参数。
为了比较Maxwell阻尼器在不同地震动强度下的耗能减震性能,图6给出了Imperial Valley(015分量)地震波作用下,峰值加速度为0.2 g、0.9 g时,布置在相邻结构顶层(结构2的顶层)的阻尼器滞回曲线。
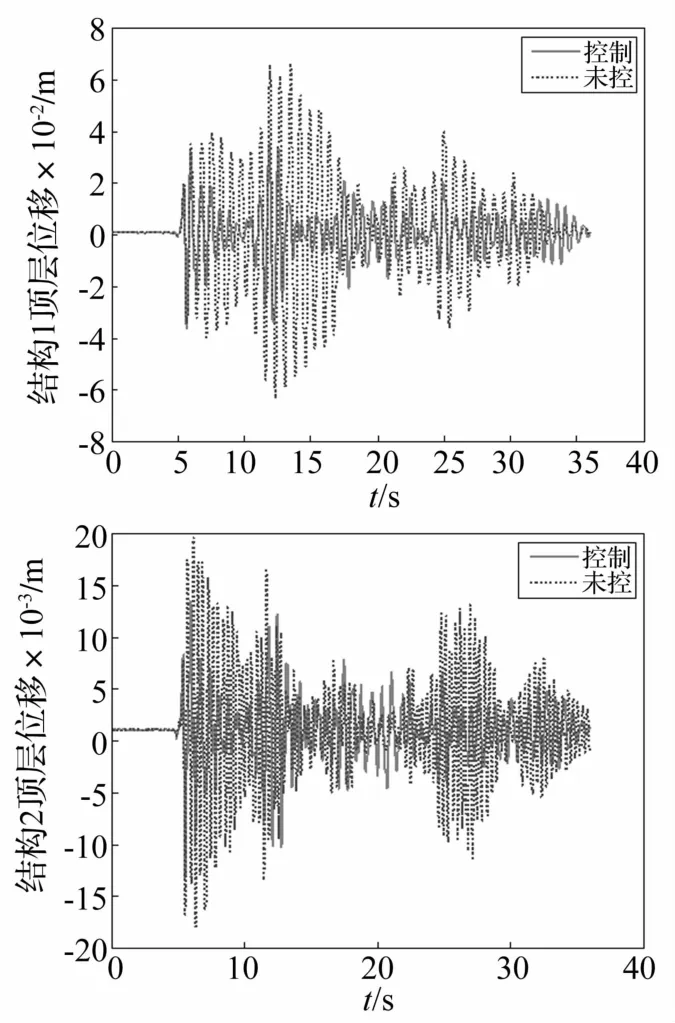
图4 相邻结构顶层位移时程(PGA=0.2 g)Fig.4 Top floor displacement time history of adjacent structures(PGA=0.2 g)

图5 相邻结构顶层位移时程(PGA=0.9 g)Fig.5 Top floor displacement time history of adjacent structures(PGA=0.9g)
由图6可以看出,在0.2 g峰值加速度作用下,阻尼器的最大输出力约为121 kN,阻尼器冲程约为±40 mm;在0.9 g峰值加速度作用下,阻尼器的最大输出力约为441 kN,阻尼器冲程约为±150 mm。阻尼器最大输出力比0.2 g加速度时的输出力增大了2.6倍,阻尼器冲程也相应增大了2.75倍,说明此时阻尼器的耗能减震作用仍十分明显。但是,此时的耗能减震效果应该主要集中在结构2,由图2、图3的IDA曲线及图5相邻结构在0.9g峰值加速度下的顶层位移时程,可以得出这一推测。
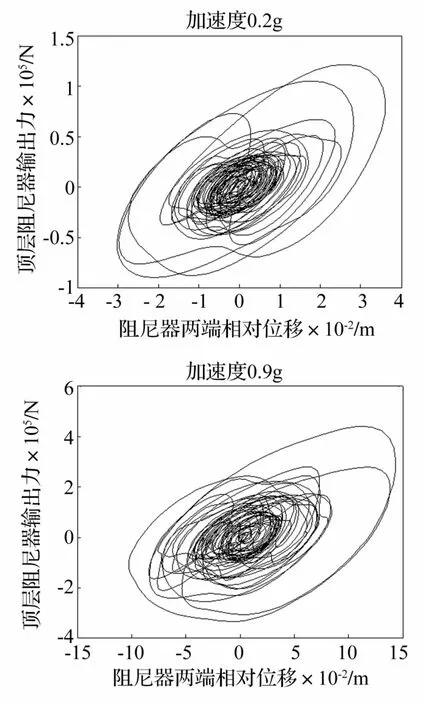
图6 相邻结构顶层阻尼器滞回曲线Fig.6 Hysteresis curves of top floor damper of adjacent structures
3.3 地震易损性分析
为了进一步研究Maxwell阻尼器优化参数控制理论对相邻结构在不同地震波作用及不同强度地震动水平下的控制效果,并能从性能评估的角度研究相邻结构在不同极限状态下的抗震性能,图7给出了相邻结构在立即使用(IO)、轻微破坏(SD)、生命安全(LS)和防止倒塌(CP)四个极限状态下的地震易损性曲线。(实线为控制下的地震易损性曲线,虚线为未控下的地震易损性曲线)
从图7可以看出,随着结构从立即使用发展到防止倒塌状态,结构的易损性曲线逐渐变的扁平,尤其是结构2,说明结构2的抗震安全性要优于结构1。
通过对比结构1在控制和未控情况下的地震易损性曲线发现,受控后的易损性曲线在立即使用(IO)和防止倒塌(CP)性能水平下与未控情况下非常接近,说明阻尼器在此性能水平下对结构1的控制效果不明显;而在轻微破坏(SD)和生命安全(LS)性能水平下的超越概率均大于未控的情况,即在此性能水平下阻尼器对结构1的动力响应反而起到了放大的作用。前述的IDA曲线和结构1在不同地震动强度下的顶层位移时程响应也可以得出相似的结论。
通过对比结构2在控制和未控情况下的地震易损性曲线,可以看出Maxwell阻尼器对结构2在各个性能极限状态下的控制效果均较好,结构2在立即使用(IO)、轻微破坏(SD)、生命安全(LS)和防止倒塌(CP)性能极限状态下的超越概率均远小于未控时的超越概率。因此,可以看出,前述不同地震动强度下顶层阻尼器滞回曲线表现出的良好的耗能能力主要是对于结构2的控制效应。
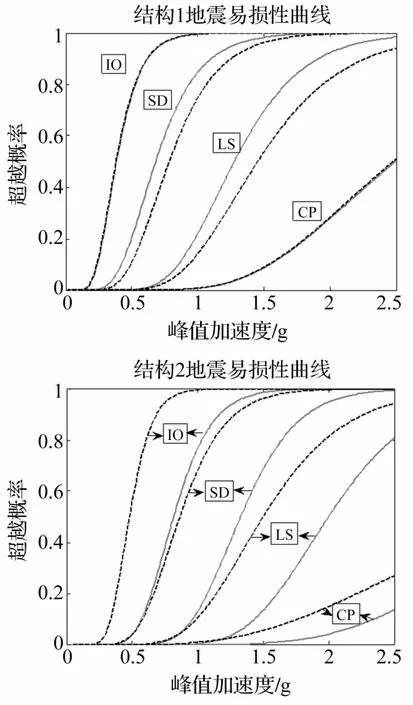
图7 相邻结构的地震易损性曲线Fig.7 Seismic fragility curves of the adjacent structures
因此,从性能评估的角度可以得出,由文献[4]计算出的Maxwell阻尼器优化参数对结构1的控制效果并不显著,有时甚至起到相反的作用;对结构2各性能极限状态下的控制效果均较好,但是对相邻结构总的控制效果的衡量有待进一步论证。
3.4 参数化分析
为了探寻相邻结构在各性能水平下均具有较为合适的阻尼器参数,本文进行了大量的、不同阻尼器参数下的增量动力分析,并基于增量动力分析得出了相邻结构在不同阻尼器参数下的地震易损性曲线。因Maxwell阻尼器刚度系数对控制效果的影响较小,本文仅研究了不同阻尼参数下相邻结构的地震易损性曲线,并以地震易损性最小为原则选取了合适的阻尼参数。图8、图9给出了相邻结构在不同阻尼参数下的地震易损性曲线。
由图8可以看出,对于结构1而言,当结构经历立即使用(IO)、轻微破坏(SD)和生命安全(LS)三个阶段时,阻尼器阻尼参数设置为1.0×104N·s/m时,结构的超越概率为最小;而在经历防止倒塌(CP)阶段时,即便将阻尼加大到1.0×106N·s/m,其超越概率与阻尼为1.0×104N·s/m和1.0×105N·s/m时的超越概率比较接近,并可以看出按照文献[4]计算出的阻尼优化参数2.4×105N·s/m下的超越概率最大。
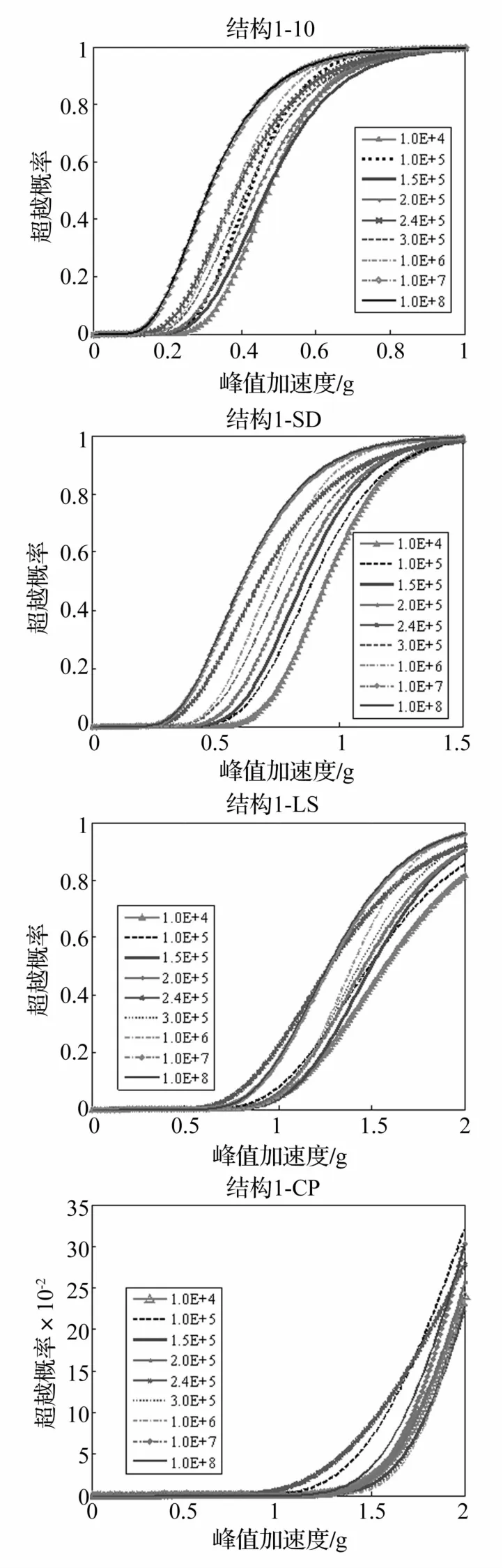
图8 结构1在不同阻尼器参数下的易损性曲线Fig.8 Fragility curves of structure 1 under different damper parameters
对于结构2,由图9可以看出,当结构经历立即使用(IO)、轻微破坏(SD)和生命安全(LS)三个阶段时,阻尼器阻尼参数设置为1.5×105N·s/m时,结构的超越概率基本为最小;而在经历防止倒塌(CP)阶段时,若将阻尼参数设置为由文献[4]计算出的优化参数2.4 ×105N·s/m,结构2的超越概率最小,设置为1.5× 105N·s/m时次之。
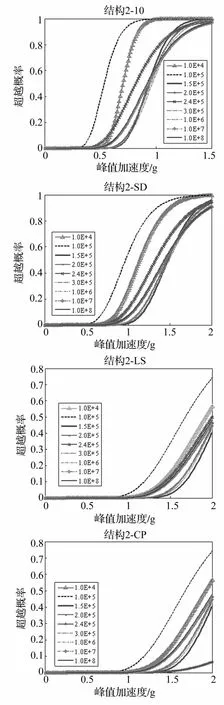
图9 结构2在不同阻尼器参数下的易损性曲线Fig.9 Fragility curves of structure 2 under different damper parameters
为了找到能同时控制两结构在不同性能水平下的超越概率的阻尼器优化参数,本文以两结构总超越概率最小为基本原则选取相邻结构较为合适的阻尼参数值。图10给出了相邻结构在不同阻尼器阻尼参数下、不同性能水平时的总超越概率曲线。
由图10可以看出,若使两结构在不同性能水平下均能得到较好的控制效果,阻尼器阻尼值可设为1.5× 105N·s/m,该值下两结构的总超越概率在不同性能水平时均较小。由图8、图9亦可以看出,该值对结构1和结构2在各性能水平下的控制效果,均优于由文献[4]计算出的2.4×105N·s/m。
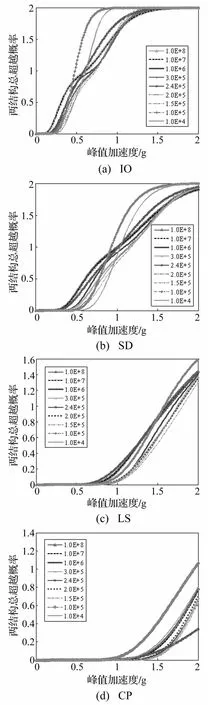
图10 相邻结构在不同阻尼器参数下的总超越概率Fig.10 Total exceeding probability of adjacent structures under different damper parameters
4 结 论
本文通过对连接Maxwell阻尼器的相邻钢筋混凝土框架结构进行20条地震动作用下的增量动力分析及地震易损性分析,研究了Maxwell阻尼器优化参数表达式在不同性能水平下的控制效果,并基于大量的参数化分析,得出了合适的阻尼器参数值。
(1)由相邻结构控制和未控下的IDA曲线和地震易损性曲线可以得出,由文献[4]计算的Maxwell阻尼器优化参数仅对结构2在各性能极限状态下有较好的控制效果;由顶层阻尼器的滞回曲线可以得出,不同强度水平下,阻尼器的耗能能力均较好,但阻尼器的控制性能主要集中于结构2。
(2)参数化分析得出相邻结构在不同性能水平下的阻尼器优化参数为1.5×105N·s/m,小于按文献[4]计算出的2.4×105N·s/m,但是该值对相邻结构在各性能水平下的超越概率均具有良好的控制效果。
[1]朱宏平,俞永敏,唐家详.地震作用下主-从结构的被动优化控制研究[J].应用力学学报,2000,17(2):63-69.
ZHU Hong-ping,YU Yong-min,TANG Jia-xiang.Optimal passive control of primary-auxiliary structures under earthquake excitation[J].Chinese Journal of Applied Mechanics,2000,17(2):63-69.
[2]朱宏平,杨紫健,唐家祥.利用连接装置控制两相邻结构的地震响应[J].振动工程学报,2003,16(1):57-61.
ZHU Hong-ping,YANG Zi-jian,TANG Jia-xiang.Control of the seismic response of two adjacent structures using a damped link[J].Journal of Vibration Engineering,2003,16(1):57-61.
[3]朱宏平,梁露.两相邻结构地震动响应被动优化控制的比较研究[J].工程力学,2005,22(增刊1):183-187.
ZHU Hong-ping,LIANG Lu.Comparative study of passive optimum control for reducing seismic responses of adjacent structures[J].Engineering Mechanics,2005,22(Sup1):183-187.
[4]朱宏平,翁顺,陈晓强.控制两相邻结构地震动响应的Maxwell模型流体减振器优化参数研究[J].应用力学学报,2006,23(2):296-300.
ZHU Hong-ping,WENG Shun,CHEN Xiao-qiang.Optimum parameters of Maxwell-defined dampers for reducing the seismic responses of adjacent structures under earthquake [J].Chinese Journal of Applied Mechanics,2006,23(2):296-300.
[5]Zhu H P,Iemura H.A study of response control on the passive coupling element between two parallel structures[J].International Journal of Structural Engineering and Mechanics,2000,9(4):383-396.
[6]Zhu H P,Iemura H.A study on interaction control for seismic response of parallel structures[J].Computers and Structures,2001,79(2):231-242.
[7]Zhu H P,Xu Y L.Optimum parameters of Maxwellmodeldefined dampers used to link adjacent structures[J].Journal of Sound and Vibration,2005,279(1-2):253-274.
[8]Zhu H P,Ge D D,Huang X.Optimum connecting dampers to reduce the seismic response of parallel structures[J].Journal of Sound and Vibration,2011,330:1931-1949.
[9]閤东东,朱宏平,陈晓强.两相邻结构地震动响应被动优化控制研究[J].振动工程学报,2008,21(5):482 -487.
GE Dong-dong,ZHU Hong-ping,CHEN Xiao-qiang.Passive optimum control for reducing seismic responses of adjacentstructures[J].Journal of Vibration Engineering,2008,21(5):482-487.
[10]Xu Y L,Zhang W S.Closed-form solution for seismic response of adjacent buildings with LQG controllers[J].Earthquake Engineering and Structural Dynamics,2002,31(2):235-259.
[11]Bhaskararao A V,Jangid R S.Seismic analysis of structures connected with friction dampers[J].Engineering Structures,2006,28(5):690-703.
[12]Bhaskararao A V,Jangid R S.Seismic response of adjacent buildings connected with friction dampers[J].Bulletin of Earthquake Engineering,2006,4(1):43-64.
[13]Bhaskararao A V,Jangid R S.Optimum viscous damper for connecting adjacent SDOF structures for harmonic and stationary white noise random excitations[J].Earthquake Engineering and Structural Dynamics,2007,36(4):563-571.
[14]Basili M,Angelis M D.Optimal passive control of adjacent structures interconnected with nonlinear hysteretic devices [J].Journal of Sound and Vibration,2007,301(1/2):106 -125.
[15]Basili M,Angelis M D.A reduced order model for optimal design of 2-mdof adjacent structures connected by hysteretic dampers[J].Journal of Sound and Vibration,2007,306(1/2):297-317.
[16]Ok S Y,Song J,Park K S.Optimal design of hysteretic dampers connecting adjacent structures using multi-objective genetic algorithm and stochastic linearization method[J].Engineering Structures,2008,30(5):1240-1249.
[17]Kasai K,Maison B F.Building pounding damage during the 1989 Loma Prieta earthquake[J].Engineering Structures, 1997,19(3):195-207.
[18]Sezen H,Whittaker A S,Elwood K J,et al.Performance of reinforced concrete buildings during the August 17,1999 Kocaeli,Turkey earthquake,and seismic design and construction practice in Turkey[J].Engineering Structures,2003,25(1):103-114.
[19]Naeim F,Lew M,Huang SC,et al.The performance of tall buildings during the 21 September 1999 Chi-Chi earthquake,Taiwan[J].The Structure Design of Tall Building,2000,9(2):137-160.
[20]Wang Z F.A preliminary report on the Great Wenchuan Earthquake[J].Earthquake Engineering and Engineering Vibration,2008,7(2):225-234.
[21]Shome N,Cornell C A.Probabilistic seismic demand analysis of nonlinear structures[R].Stanford:Stanford University.
[22]吴巧云,朱宏平,樊剑.基于性能的钢筋混凝土框架结构地震易损性分析[J].工程力学,2012,29(9):117-124.
WU Qiao-yun,ZHU Hong-ping,FAN Jian.Performancebased seismic fragility analysis of RC frame structures[J].Engineering Mechanics,2012,29(9):117-124.
[23]Wu Qiao-yun,Zhu Hong-ping,Fan Jian.Performance-based seismic financial risk assessment of reinforced concrete frame structures[J].Journal of South University,2012,19:1425-1436.
[24]高层建筑混凝土结构技术规程JGJ3-2002[S].北京:中国建筑工业出版社,2002.
[25]FEMA 356.Prestandard and Commentary for Seismic Rehabilitation of Buildings[S].Prepared by ASCE for Federal Emergency Management Agency,Washington,D.C.,USA,2000.
Seism ic fragility analysis of two ad jacent structures connected w ith M axwell dampers
WU Qiao-yun1,2,ZHU Hong-ping2,CHEN Chu-long2
(1.School of Resource and Civil Engineering,Wuhan Institute of Technology,Wuhan 430073,China;2.School of Civil Engineering and Mechanics,Huazhong University of Science and Technology,Wuhan 430074,China)
A two-dimensionalmodel of two adjacent reinforced concrete frames connected with Maxwell dampers was set up considering the nonlinear behavior of beam-column elements and damper ones under major earthquakes.Through a lot of incremental dynamic analysis(IDA),the applicability of Maxwell damper optimal parameters theoretical expressions in thewhole process from initial elastic,yield to final collapse of the structureswas investigated.Based on the results of IDA,the comparative analysis of seismic fragility curves of the structures with control and without control was done.From the perspective of performance evaluation,the control effects of Maxwell dampers on the two adjacent structures were studied under different seismic waves and different seismic intensities.Through time history analysis of top floor displacements of the adjacent structures under different seismic intensities,it was shown that the control effects of Maxwell dampers on the top floor displacements of the two adjacent structures are good under small earthquakes;however,under big earthquakes,only the second structure can be controlled significantly;the control effects ofMaxwell dampers on the second structure under each performance level are superior to those on the first structure.Finally,through a large number of parametric analyses and based on the principle of the minimum seismic fragility of adjacent structures,the suitable parameter values of Maxwell damperswere proposed.
adjacent structures;seismic fragility;Maxwell damper;incremental dynamic analysis(IDA);performance level
TU311.3;TU375.4
A
10.13465/j.cnki.jvs.2015.21.028
湖北省教育厅科研项目(Q20141503);国家自然科学基金(51408443)
2014-01-26 修改稿收到日期:2014-09-25
吴巧云女,博士后,副教授,1985年生
朱宏平男,博士,教授,1965年生

