耦合小波变换和偏最小二乘的悬浮物浓度和浊度高光谱建模方法

曹 引，冶运涛，赵红莉，石玉波，蒋云钟

（1.东华大学 环境科学与工程学院，上海 201620；2.中国水利水电科学研究院 水资源研究所，北京 100038；3.水利部 水资源司，北京 100053）

耦合小波变换和偏最小二乘的悬浮物浓度和浊度高光谱建模方法

曹 引1，2，冶运涛2，赵红莉2，石玉波3，蒋云钟2

（1.东华大学 环境科学与工程学院，上海 201620；2.中国水利水电科学研究院 水资源研究所，北京 100038；3.水利部 水资源司，北京 100053）

针对高光谱曲线中可能存在噪声以及传统半经验方法不能有效利用全部光谱信息的问题，提出了耦合Haar小波变换和偏最小二乘的水质遥感高光谱建模方法（HaarWT-PLS）。利用该方法，对在南四湖获取的实测高光谱数据经分解尺度为3的Haar小波变换后，将原始光谱数据压缩到47个特征变量；随后利用小波变换重构的光谱数据建立了悬浮物浓度和浊度的HaarWT-PLS反演模型，并进行了验证。结果表明：HaarWT-PLS反演悬浮物浓度和浊度精度较高，验证样本的均方根误差分别为25.05 mg/L和20.10NTU，平均相对误差分别为20.36%和13.88%。通过和单波段模型、一阶微分模型和波段比值模型进行精度对比分析，本文建立的Haar WT-PLS模型反演悬浮物浓度和浊度具有较高的精度和更好的稳定性。

小波变换；偏最小二乘法；高光谱；悬浮物；浊度；南四湖

1 研究背景

内陆水体重要水质参数悬浮物浓度和浊度的传统监测手段是采用现场采样、实验室分析等，无法满足大范围、多时相的水质监测的实际需求［1-2］，而遥感技术可以弥补以上地面监测手段的不足［3］。遥感高光谱技术能够显著提高水质参数反演的精度，从而成为水质遥感研究领域的热点和重点［4］。

目前高光谱水质参数反演的半经验［4-8］、半分析［9-10］和物理分析等方法［11］仅使用单波段或几个波段信息，可能会舍弃其他波段的有价值信息，对提高反演精度有一定影响。偏最小二乘法（Partial Least Square，PLS）为解决上述问题提供了一条有效途径［12］，受到研究者的高度关注，如杨燕明等［13］利用PLS方法较高精度地反演了黄海水体叶绿素、南海水体叶绿素和泥沙，证明了PLS能够处理多变量少样本的问题；徐京萍等［14］用PLS模型提取了石头口门水库水体叶绿素a浓度和悬浮物浓度，发现该模型比传统半经验模型优势明显；刘忠华等［15］利用db小波变换和PLS反演巢湖悬浮物浓度，并验证了其具有较高精度；Lu［16］和Song［17］等用遗传算法选择和叶绿素a浓度比较敏感的波段或波段组合，建立长春石头口门水库叶绿素a浓度的GA-PLS反演模型，与三波段反演模型对比，具有更高的精度和空间移植性。杨燕明等［13］和徐京萍等［14］直接用原始光谱反射率建立水色要素反演模型，没有对原始光谱去噪、压缩。

本文在国内外研究成果基础上，以南四湖悬浮物浓度和浊度同步遥感反演为研究对象，选择Haar小波变换处理原始光谱，与db正交小波相比，利用Haar小波能实现信号的快速分析和重构且不会产生相位失真［18］，在此基础上，提出了耦合Haar小波变换和偏最小二乘的高光谱建模方法（Haar⁃WT-PLS），建立南四湖水体悬浮物浓度和浊度反演模型，并和常规的单波段法、波段比值法和一阶微分法进行比较分析，同时评价了本文建立模型的精度及其适用性。

2 研究区概况及数据获取

2.1研究区概况南四湖位于山东省西南部，由微山湖、昭阳湖、独山湖、南阳湖等4个湖组成，全湖面积1 266 km2，流域面积3.17万km2，是我国大型淡水湖之一，也是南水北调东线工程重要的水源地和调蓄湖泊，兼有防洪、抗旱、灌溉、供水、养殖及旅游等一系列功能。2014年以来，山东发生严重旱情，南四湖水位不断下降，分别降至死水位和最低生态水位，水位持续降低，造成水面和湿地面积不断的缩小，水温变化剧烈，水体自净能力下降，水质恶化，严重影响南四湖附近居民的日常生活和养殖业。对南四湖水质进行监测对保障南四湖周边居民的饮用水安全以及对南水北调东线工程的顺利实施具有重大意义。

2.2实验数据获取2014年7月21—23日，在南四湖布设了15个采样点，对水面进行光谱测量，同时对表层水进行取样，迅速带回实验室测定悬浮物浓度。采样期间天空云量非常少，风速较小，水面也较为平静，无大面积蓝藻爆发，采样站点分布如图1所示。光谱测量采用SVC公司生产的HR-1024地物光谱辐射计。浊度用美国哈希HACH浊度仪1 900 C现场测量，悬浮物浓度测量采用过滤烘干法，先将滤膜置于105℃烘箱中烘干2 h，除去水分并称重，然后用称重后滤膜过滤水样后于105℃烘干2 h再次称重，将两次重量相减，除以过滤水样体积，即求得总悬浮物质量浓度。剔除光谱异常值后选取12个样点进行分析，选择8个点进行建模，剩下4个用于验证。

图1 采样点分布图

3 耦合Haar小波变换和偏最小二乘的水质遥感高光谱建模方法（HaarWT-PLS）

Haar WT-PLS建模方法是在Haar小波变换（WT）和偏最小二乘法（PLS）基础上提出，其建模思路是将原始光谱信息经Haar小波变换后的数据输入PLS建模。

3.1小波变换Haar小波变换对原始光谱信号去噪、压缩及重构流程如图2所示。

3.2PLS建模PLS建模过程如图3所示。假定有样本数为n、自变量个数为p的自变量矩阵X（n×和因变量个数为q的因变量矩阵首先，分别用变量与均值之差除以标准差进行标准化处理，这样可以加快计算速度，尽量避免数据的舍入误差。标准化处理后得到矩阵其次，分别求出E0和F0的最大特征值和最大特征值对应的特征向量，提取第一个主成分t1，要求t1在携带E0的绝大部分信息的同时能够对F0也有最大的解释能力，分别计算X和Y对t1的回归方程，检验回归方程是否达到既定的精度，若满足精度要求，算法终止，否则分别计算E0和F0的残差矩阵E1和F1，提取第二个主成分，如此循环，到满足精度要求为止。图3中SSh和PRESSh分别指因变量y在两种不同的模型下的预测误差平方和，用提取的主成分和F0建立回归模型。

图2 小波变换流程图

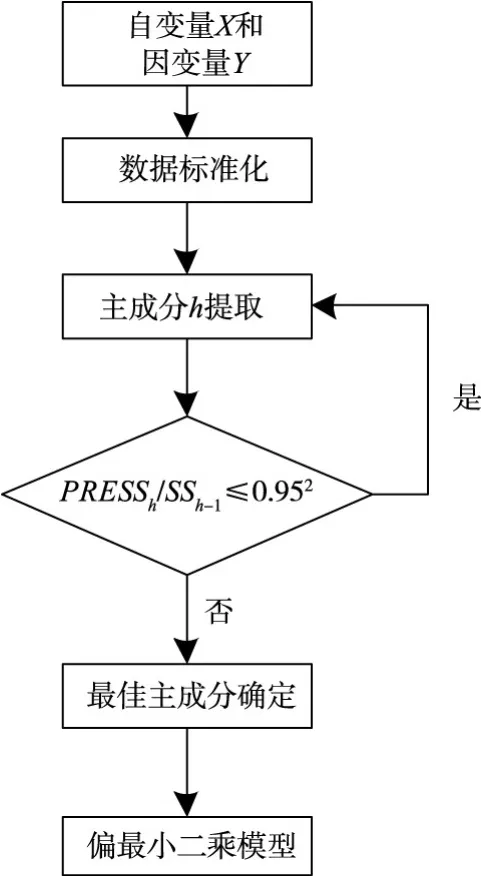
图3 PLS建模流程图

3.3交叉有效性检验PLS建模中选择的最佳主成分个数可以根据交叉有效性检验确定，假定样本i的预测值用yi表示，用全部样本提取h个成分进行回归分析建模，第i个样本模型预测值用yˆh-i表示，去除样本i用剩余的样本提取h个主成分进行回归建模，第i个样本模型预测值用表 示，则：

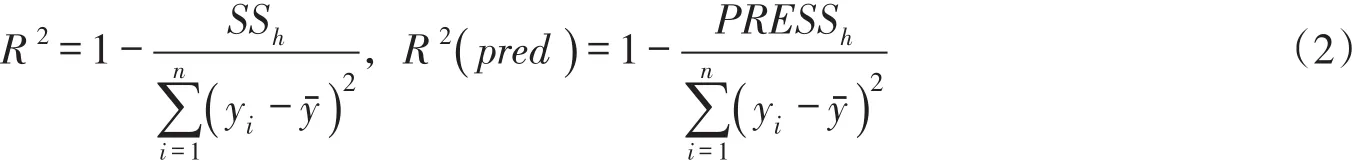
3.4主成分解释能力分析PLS从自变量X中提取的主成分信息和因变量Y有很强的相关性，能够很好地解释X和Y包含的信息，具体方法参阅文献［19］。

4 基于HaarWT-PLS方法的悬浮物浓度和浊度反演

4.1光谱特征分析南四湖水体悬浮物浓度值和浊度值变化范围分别为16～210 mg/L和39.5～338NTU，变化范围较大，平均值分别为98.55 mg/L和147.97 NTU，光谱测量结果如图4所示。从图4中可以看出，由于叶绿素a和黄色物质对400～500 nm波长范围内光的强吸收导致该范围内的水体反射率普遍偏低；560 nm附近的反射峰与叶绿素、胡萝卜素的弱吸收和细胞、悬浮物的散射作用有关，可用于叶绿素a是否存在的判定依据；因为叶绿素在红光波段的强吸收，使680 nm附近出现另一吸收峰；700 nm附近出现的反射峰是含藻类水体一个重要光谱特征，可以将其当作藻类叶绿素存在的定量化判定标志［20］；纯水在大于730 nm的波段范围内吸收作用迅速增强，导致水体光谱反射率降低；悬浮物散射作用使得在810 nm附近形成了又一反射峰，其位置随悬浮物浓度的增加由短波向长波方向移动，这就是“红移现象”［21］。

4.2光谱曲线Haar小波变换本文选择400～900 nm范围内共370个波段反射率，采用Haar小波对其不同尺度分解，分解尺度越大造成分解后小波系数越少，意味着越大的数据压缩程度。如何选择分解尺度需要结合信息保留量、特征变量个数以及总均方根误差（TRMSE）3个指标［15］来考虑。其中TRMSE用式（3）计算。

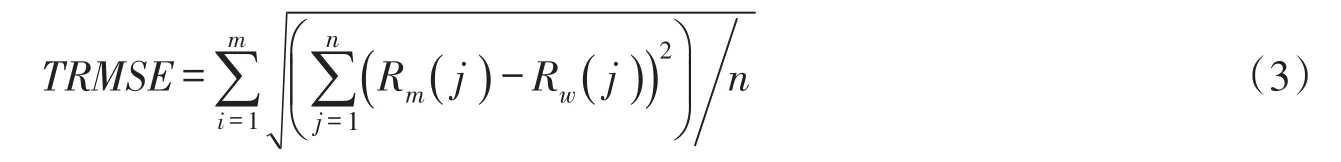
式中：m为样点个数；n为波段个数；Rm（j）和Rw（j）分别表示原始光谱反射率和小波重构后的光谱反射率。

利用Haar小波变换对原始光谱反射率进行5种尺度（包括2、3、4、5、6）分解，得到高频和低频系数，将小于某一阈值的高频系数置为零，实现光谱数据去噪，同时保留其他系数重构光谱曲线。不同尺度分解后的指标见表1。若PLS建模的波长数远多于样本点数，会增大模型的不确定性［22］，因此在保留原始光谱信息的基础上，尽可能最大程度地压缩光谱数据，对比表1中不同分解尺度下原始光谱信息保留量、特征变量个数以及TRMSE，最终选择分解尺度为3的Haar小波变换，其分解后的47个特征变量携带原始光谱99.95%的信息，在此基础上重构后的光谱反射率如图5所示。由图5看出，重构光谱曲线与原始光谱曲线的趋势、波峰和波谷位置保持了很好的一致性。

表1 原始光谱小波分解后指标统计

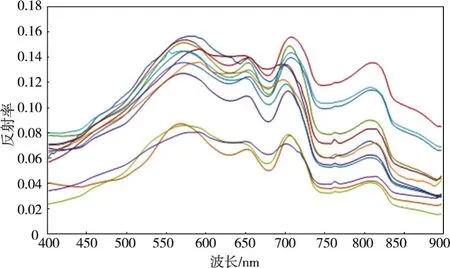
图4 水体采样点光谱曲线

图5 小波重构后的光谱数据

4.3 HaarWT-PLS建模

4.3.1 最佳主成分个数的确定 选择用于建模的8个点的光谱数据经Haar小波变换后的特征变量作为自变量；以8个点的悬浮物浓度和浊度作为因变量。用MATLAB（2013a）编写偏最小二乘程序，得到随主成分增加反演悬浮物浓度和浊度的HaarWT-PLS模型的R2和R2（pred）变化图，如图6所示，经交叉有效性检验，确定最佳主成分个数为3个，此时悬浮物浓度和浊度反演模型的R2分别为0.9587和0.9163，R2（pred）分别为0.7379和0.8911。

4.3.2 主成分解释能力分析 不同主成分对X、Y的解释能力见表2。3个主成分累积解释了自变量X99.18%的信息和自变量Y93.57%的信息，说明利用HaarWT-PLS建立的模型不仅能够携带自变量几乎全部信息，而且对因变量具有很高的解释水平。

图6 最佳主成分个数确定

表2 各主成分对X、Y的解释能力

4.3.3 模型验证 利用剩余4个点检验模型的预测精度，预测精度用均方根误差RMSE和平均相对误差ARE表示，如式（4）和式（5）所示。验证结果见表3和表4。

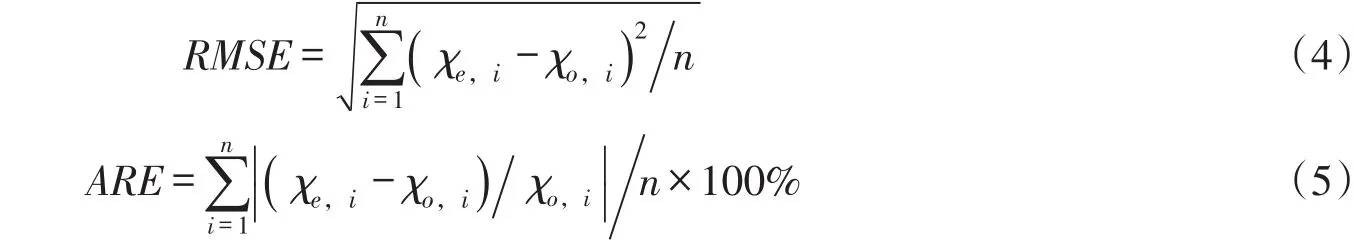
式中：χe，i为第i个预测值；χo，i为第i个实测值；n为样本数。

表4 浊度预测值与实测值比较

图7 各波段系数图

图8 悬浮物浓度和浊度线性回归模型

4.3.4 各波段回归系数分析 反演悬浮物浓度和浊度的Haar WT-PLS模型各波段回归系数如图7所示，可以看出悬浮物浓度和浊度反演模型在400～900 nm范围内的回归系数变化具有一致性，这是因为南四湖水体悬浮物浓度和浊度具有较高的相关性，两者相关系数达0.9651（决定系数R2为0.9315），散点图如图8所示。悬浮物浓度和浊度Haar WT-PLS反演模型中730～900 nm光谱波段的回归系数变化不大，表明该波长范围内各光谱波段对模型的贡献相对均衡，这是因为该波段范围内光谱反射率主要受悬浮物散射作用影响。

5 模型对比与评价

利用建立的反演悬浮物浓度和浊度常用的单波段、一阶微分和波段比值模型与Haar WT-PLS模型验证结果进行比较，其中悬浮物浓度和浊度反演模型验证结果分别见表5和表6。

表5 悬浮物浓度反演模型对比

表6 浊度反演模型对比

由表5可以看出，HaarWT-PLS模型反演悬浮物浓度具有较高的精度，模型R2为0.9587，仅次于R756/R748波段比值模型，但验证样本的RMSE和ARE均低于3种半经验模型；由表6可以看出Haar⁃WT-PLS浊度反演模型的R2和R838单波段模型、R731/R720波段比值模型的R2相差不大，低于R′781一阶微分模型的R2，但其验证样本的RMSE还是ARE都远低于其他3种模型，表现出较高的预测精度和稳定性，R′781一阶微分模型虽然模型的R2较大，但验证样本误差相对较大，这是因为一阶微分对噪声十分敏感，模型预测能力较弱。综上分析，对比其他3种模型，本文建立的HaarWT-PLS模型能充分利用光谱信息，反演悬浮物浓度和浊度具有较高的精度和更好的稳定性，可为未来用高光谱数据进行水体水质参数反演提供一种研究方法。但可能与样本数偏少和水质高光谱遥感反演难度大有关，HaarWT-PLS模型总体精度依旧不高，个别样本精度较低，为进一步提高反演精度，还需在以后的工作中进行大量采样，以研究提出方法的特性和适用性。

［1］ 张运林，秦伯强，陈伟民，等.悬浮物浓度对水下光照和初级生产力的影响［J］.水科学进展，2004，15（5）：615-620.

［2］ Boderick E，Warnock.Regional and seasonal differences in light absorption by yellow substance in Southern Bright of North Sea［J］.Journal of Sea Research，1999，142：149.

［3］ 疏小舟，尹球，匡定波.内陆水体藻类叶绿素浓度与反射光谱特征的关系［J］.遥感学报，2000，4（1）：41-45.

［4］ 宋庆君，马荣华，唐军武，等.秋季太湖悬浮物高光谱估算模型［J］.湖泊科学，2008，20（2）：196-202.

［5］ 陈建辉，徐涵秋.晋江水体悬浮物浓度的高光谱建模分析［J］.遥感技术与应用，2008，23（6）：653-357.

［6］ 杨婧茹，臧淑英，惠洪宽.松花江哈尔滨段总悬浮物浓度高光谱估测模型研究［J］.安全与环境学报，2014，14（2）：239-243.

［7］ Katlane R，Nechad B，Ruddick K，et al.Optical remote sensing of turbidity and total suspended matter in the Gulf of Gabes［J］.Arab J Geosci，2013，6：1527-1535.

［8］ Chen S S，Fang L G，Zhang L X，et al.Remote sensing of turbidity in seawater intrusion reaches of Pearl River Estuary-A case study in Modaomen water way，China［J］.Estuarine，Coastal and Shelf Science，2009，82：119-127.

［9］ 施坤，李云梅，刘忠华，等.基于半分析方法的内陆湖泊水体总悬浮物浓度遥感估算研究［J］.环境科学，2011，32（6）：1571-1580.

［10］ Sun D Y，Li Y M，Le C F，et al.A semi-analytical approach for detecting suspended particulate composition in com⁃plex turbid inland waters（China）［J］.Remote Sensing of Environment，2013，134：92-99.

［11］ 李云梅，黄家柱，陆皖宁，等.基于分析模型的太湖悬浮物浓度遥感监测［J］.海洋与湖沼，2006，37（2）：171-177.

［12］ 王惠文，吴载斌，孟洁.偏最小二乘回归的线性与非线性方法［M］.北京：国防工业出版社，2006.

［13］ 杨燕明，刘贞文，陈本清，等.用偏最小二乘法反演二类水体的水色要素［J］.遥感学报，2005，9（2）：123-130.

［14］ 徐京萍，张柏，宋开山，等.用偏最小二乘法提取石头口门水库水色信息［J］.中国科学院研究生院学报，2007，24（6）：814-819.

［15］ 刘忠华，李云梅，吕恒，等.基于偏最小二乘法的巢湖悬浮物浓度反演［J］.湖泊科学，2011，23（3）：357-365.

［16］ Lu D M，Song K S，Li L，et al.Training a GA-PLS Model for Chl-a Concentration Estimation over Inland Lake in Northeast China［J］.Procedia Environmental Sciences，2010（2）：842-851.

［17］ Song K S，Lu D M，Li L，et al.Remote sensing of chlorophyll-a concentration for drinking water source using genet⁃ic algorithms（GA）-partial least square（PLS）modeling［J］.Ecological Informatics 2012，10：25-36.

［18］ 米晨，汤秀芬，魏凤兰.基于Haar小波变换的图像分解与重构［J］.实验室研究与探索，2003，22（2）：78-81.

［19］ 葛彦鹏.基于偏最小二乘法的火电机组关键参数预测模型研究［D］.北京：华北电力大学，2012.

［20］ 焦洪波，查勇，李云梅，等.基于高光谱遥感反射比的太湖水体叶绿素a含量估算模型［J］.遥感学报，2006，10（2）：242-248.

［21］ 王艳娇，张培群，董文杰，等.悬浮泥沙反射光谱特性和泥沙量估算试验研究［J］.泥沙研究，2007，（5）：36-41.

［22］ 褚小立，田高友，袁洪福，等.小波变换结合多维偏最小二乘方法用于近红外光谱定量分析［J］.分析化学，2006，34：175-178.

Hyperspectral modeling method of suspended solid concentration and turbidity based on the coupling of Haar wavelet transform and partial least squares

CAO Yin1，2，YE Yuntao2，ZHAO Hongli2，SHI Yubo3，JIANG Yunzhong2（1.School of Environmental Science and Engineering，Donghua University，Shanghai 201620，China；
2.Department of Water Resources，China Institute of Water Resources and Hydropower Research，Beijing 100038，China；3.Department of Water Resources Management，Ministry of Water Resources，Beijing 100053，China）

Aiming at the noise in hyperspectral curve and the problems that traditional semi-empirical methods cannot effectively use all effective spectral information，hyperspectral modeling method of suspended solid con⁃centration and turbidity based on the coupling of Haar wavelet transform and partial least squares（Haar wavelet transform）is proposed.Firstly，the original spectral data of Nansi Lake on July 22 to 23，2014are com⁃pressed to 47 feature variables using wavelet transform with the wavelet function Haar and decompose scale 3. Secondly，according to the reconstruction data of spectra using wavelet transform，Haar WT-PLS inversion mod⁃els of suspended solid concentration and turbidity are established and verified.The results show that inversion of suspended solid concentration and turbidity using Haar WT-PLS has higher accuracy and the root mean square errors of validation samples are 25.05 mg/L and 20.10 NTU，respectively.The average relative errors are 20.36%and 13.88%，respectively.Through the analysis and comparison of single band model，the first deriva⁃tive model，band ratio models and Haar WT-PLS model，Haar WT-PLS model proposed in the paper has high⁃er accuracy and stability to retrieve suspended solid concentration and turbidity.

wavelet transform；partial least squares；hyperspectral；suspended solid；turbidity；Nansi Lake

：Adoi：10.13244/j.cnki.jiwhr.2015.03.014

1672-3031（2015）03-0233-07

（责任编辑：韩 昆）

2015-01-20

“十二五”国家科技支撑计划课题（2013BAB05B01）；高分辨率对地观测系统重大专项（08-Y30B07-9001-13/15-01）；国家自然科学基金项目（51309254，51209223）；中国水利水电科学研究院科研专项（资基本科研1401）

曹引（1991-），男，安徽滁州人，硕士生，主要从事流域水环境定量遥感研究。E-mail：yinc0416@163.com

冶运涛（1983-），男，河南许昌人，高级工程师，博士，主要从事数字流域、流域水循环模拟及其要素定量遥感与水资源调度评价方面的研究。E-mail：yeyuntao@iwhr.com