顾及开挖深度的灰色系统模型在基坑沉降预测中应用*

孙 蕾，陈慧香

(沈阳市房产测绘中心，辽宁沈阳 110000)

0 引言

近年来，大量高层建筑以及地下工程的出现，使得基坑的数量越来越多，随着基坑开挖的深度逐步加大，基坑的支护结构、坑底等受到来自各方面的荷载明显增大，而且施工期内受降水等气候条件影响会引起基坑周边土体含水量、自重、地下水位升降等变化，这些都会导致基坑的围护结构发生不规则的水平及竖直方向的位移、坑底隆起、变形过大、土体下沉等问题，甚至导致整个基坑坍塌，造成严重的工程事故［1，2］。所以，对基坑进行安全、稳定、系统的监测，保证基坑自身支护结构和周边建筑的安全，对保护人们的生命财产安全有重大的意义。

长期以来，针对基坑变形预测的研究有很多，主要有时间序列分析、多元线性回归分析、神经网络、卡尔曼滤波、灰色系统以及混沌理论等方法。其中胡友健［3］等通过对基坑监测数据的处理，建立灰色预测模型，并开发了深基坑预测报警系统;肖芝兰［4］等在土钉支护变形预测中采用灰色预测方法，取得了较好的效果;张福民［5］等采用灰色模型与马尔可夫链结合方法对深基坑进行变形预测;冯志［6］等基于灰色系统模型实现对变形体上相互关联的多点变形预测模型的建模和预测。

由于基坑的变形受各种因素的影响，可以看做一个灰色系统，灰色系统理论对变形监测的短时间数据建模，有一定的优越性，提供了在信息不多的情况下解决变形预测的一种新途径［7，8，9］。以往的预测方法中大部分考虑以监测数据的时间序列关系而建立，但是在基坑开挖过程中，基坑的开挖深度与时间不一定成比例，从而会影响模型的精确性［10，11］。本文基于灰色系统理论建立监测数据与基坑开挖深度之间的关系模型，建立了顾及开挖深度的灰色系统分析预测模型，并通过实验数据分析，验证了灰色系统预测模型在基坑开挖过程中沉降预测精度较高，可以指导后续工程应用。

1 基本模型

1.1 数据预处理

设序列 X(0)={x(0)(k1)，x(0)(k2)，…，x(0)(kn)}，若间距Δki=ki－ki－1不为常数，称X(0)为非等间距序列。非等间距序列主要有两种路线，一种是通过各种插值的方法将其变为等间距序列，另一种是通过对间距加权。本文采用插值的方法将序列变为等间距序列，利用线性插值的方法对原始数据预处理，得到新的观测序列X(0)。

1.2 离散灰色系统模型

原始灰色系统模型对数据进行处理的过程中，微分方程和差分形式分别为连续方程和离散方程，预测时需要将两者结合在一起，这会导致离散形式到连续形式的数据跳跃，影响模型的精度，采用离散灰色系统模型可以较好地解决这个问题。

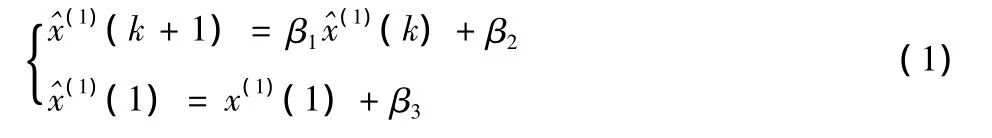
DGM(1，1)模型的最小二乘估计参数满足:

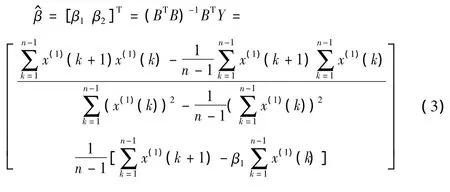
采用无约束优化模型:

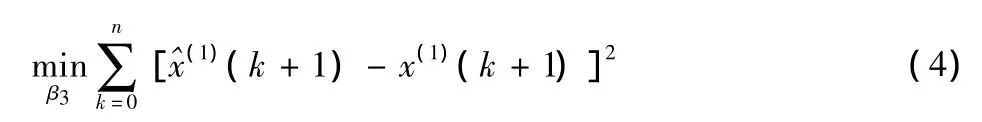
可得起始点优化参数β3的估计值为:

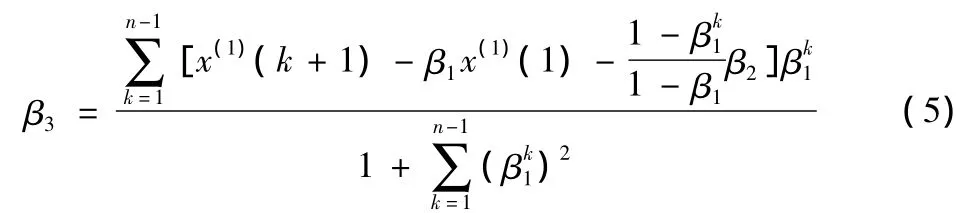
可得DGM(1，1)模型递推函数为:

式中:k=1，2，…，n － 1。

还原值为:

式中:k=1，2，…，n － 1。

2.2.1 专家的积极性 以回收应答率表示专家积极性，即专家对本研究的投入程度。本研究第1轮咨询专家应答率为93%，1名专家因出国未及时应答，第2轮咨询专家应答率为100%。

当k＜n时，称^x(0)k为模型模拟值;当k=n时，称 ^x(0)k为模型滤波值;当k＞n时，称^x(0)k为模型预测值。

1.3 模型精度的检验

在模型建立之后，要对所建立的模型进行检验，只有通过检验的模型才可以进行预测。灰色系统模型检验的方法通常有3种:相对误差检验、关联度检验和后验差检验。本文采用后验差方法来检验模型的精度。

计算残差得:原始序列X(0)以及残差序列E的方差分别为S21和S22，有:

小误差概率为:

指标C和p为后验差检验的重要指标。指标C越小，模型越精确，而C越小表明S1大S2小。S1大表示原始数据方差大，也即原始数据离散程度大;S2小表示残差方差小，即残差离散程度小。指标p越大模型越精确，p越大表明残差与残差平均值之差小于给定值0.6745 S1的点较多，即拟合值分布比较均匀。具体C和p指标评定模型精度，如表1所示。

表1 模型精度评定指标Tab.1 Accuracy evaluation indexs of model

1.4 残差修正

根据DGM(1，1)模型建模原理，对所得的序列E进行建模，建立DGM(1，1)模型，并对原来的模型进行修正，修正后的预测值为:

2 实例分析

以南京某基坑开挖为例，在该基坑周围区域设立地面变形监测点进行监测，其沉降观测使用徕卡电子水准仪及其配套使用的条码式铟钢尺，精度为三等水准测量，每次观测尽量做到了人员相对固定、仪器设备固定、固定测站数“三固定”的作业方法，测量精度满足规范要求，已经取得大量的原始观测数据。

由于基坑采用分段开挖的方法，所以基坑的整体开挖深度不同，本文开挖深度指与某一高层建筑物相邻的基坑一侧的开挖深度。取基坑旁边某高层建筑物上一监测点位W6，本次共进行了15个期次监测。其中随开挖深度增加原始累计沉降量，如表2所示。

表2 原始累计沉降量Tab.2 The original accumulated settlements

2.1 数据处理及预测

根据前文所建立的DGM(1，1)模型来对原始数据进行分析处理，为了提高模型的预测精度，分别选用前7期数据建立灰色系统模型，并根据模型预测后8期的沉降情况，并以此验证该模型用于估计开挖深度的基坑变形监测中的合理性与正确性。处理后的曲线与原始累计沉降曲线见图1，该模型预测后的残差见图2。经计算，后8期的模型预测值如表3所示。

图1 模型预测值与累计沉降曲线图Fig.1 Values predicted by model and cumulative settlement curves

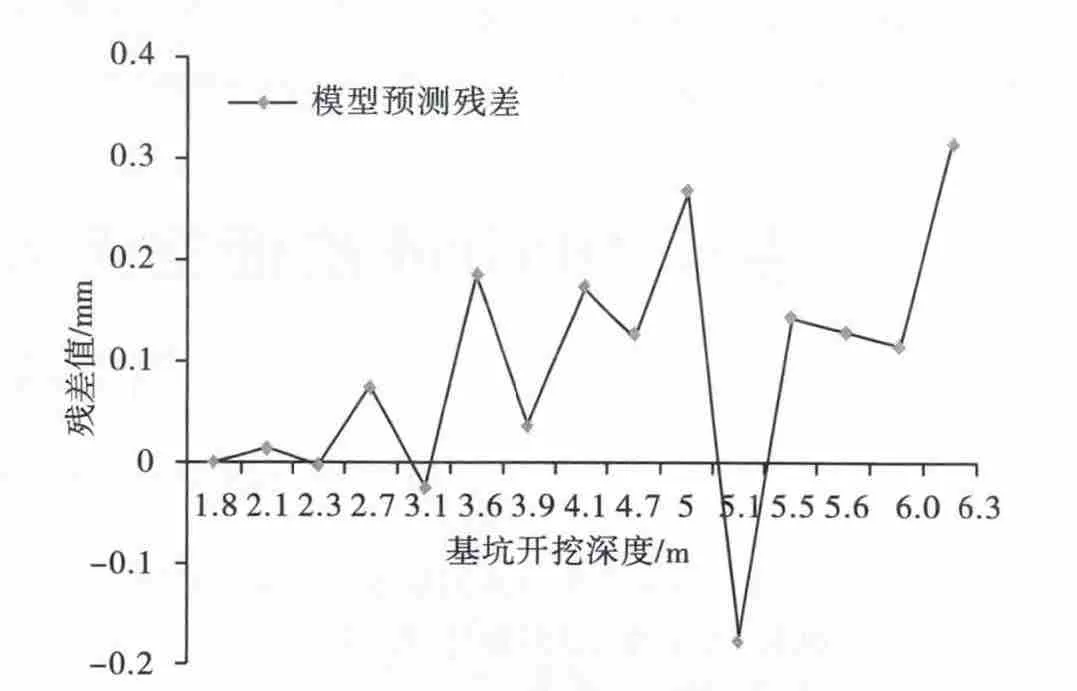
图2 模型残差值Fig.2 Model residual errors

表3 原始累计沉降与预测值对比Tab.3 Compraison between original accumulated settlement values and predicted values

2.2 结果分析

预测数据以前7次的数据来建立灰色系统模型，通过数据的新陈代谢，减少了数据的冗余，提高了模型预测的精度。经过计算C=0.04＜0.35，p=1，说明该模型的预测等级较好，可以较好的应用到基坑的变形监测过程中。另外，由图1和图2可以看出，经灰色系统模型预测后的曲线图与原始累计沉降曲线基本吻合，能较好地反映该基坑的变形情况并能及时做好预测，且本文所建立的灰色系统模型预测残差比较小，均在±0.5 mm以内。从后8期的数据还可得出，该模型预测的中误差为0.068 mm，说明预测精度相对较高，预测结果比较准确，可以较好的为基坑进行沉降预报。

3 结束语

本文通过研究顾及开挖深度的灰色系统模型在基坑沉降预测中的应用，得出如下结论:

1)原使观测数据中基坑的开挖深度是非等间距的，通过线性插值的方法对其相应的沉降数据进行处理，得到等间距的开挖深度所对应的沉降数据，并在此基础上建立DGM(1，1)模型，且模型预测精度较高，能较好地反应基坑的变形情况。

2)离散系统的灰色系统预测模型所需要的样本数据较少，预测精度较好，当有新的实测数据时，要及时对预测模型的模型参数进行更新，以提高预测精度。

3)根据本文的分析可知，灰色系统模型可以较好的应用到基坑开挖过程的沉降监测分析与预报中，且在顾及开挖深度的灰色系统模型中预测结果有较小的残差，预测结果具有一定的参考价值。

［1］黄传胜.地铁深基坑开挖变形预测方法及工程应用研究［D］.长沙:中南大学，2011.

［2］王强，刘松玉，童立元，等.灰色理论在深基坑支挡结构变形预测中应用［J］.岩土工程学报，2010(S2):69－72.

［3］胡友健，谭先康.深基坑工程监测数据处理与预测报警系统［J］.焦作工学院学报，2001，20(2):130 －135.

［4］肖芝兰，曾庆响.土钉支护变形的灰色预测方法［J］.五邑大学学报:自然科学版，2002，16(2):71 －75.

［5］张福民，崔桂林.基于灰色马尔可夫链的深基坑沉降预测［J］.土工基础，2006，20(4):82 －84，93.

［6］冯志，李兆平，李祎.多变量灰色系统预测模型在深基坑围护结构变形预测中的应用［J］.岩石力学与工程学报，2007(S2):4 319－4 324.

［7］郑加柱，光辉.顾及开挖深度的卡尔曼滤波模型在基坑变形分析中的应用［J］.测绘通报，2009(5):49 －51，68.

［8］李斌，朱健.非等间隔灰色GM(1，1)模型在沉降数据分析中的应用［J］.测绘科学，2007(4):52 －55，194.

［9］唐争气，谭志强.灰色时序组合模型在基坑监测中的运用［J］.测绘工程，2014(2):49－53.

［10］覃东.改进的GM(1，1)模型在公路隧道沉降预测中的应用［J］.北京测绘，2014(1):49 －51，74.

［11］万志辉，刘红艳，步艳洁.基于灰色理论的深基坑围护结构变形预测研究［J］.辽宁工业大学学报:自然科学版，2014(3):187－189.