“再创造”教学策略研究
楼跃军
【摘 要】让学生用“再创造”方法去学习数学是我们教师首先要考虑的核心问题。因此,要激发学生再创造的动机,放手让学生进行自主探索,并且要学会猜想,去体会发现、创造数学知识的感受,增强学生的创新意识和实践能力。
【关键词】再创造;激发动机;自主探索;猜想
学生“再创造”理论是荷兰著名数学家弗赖登塔尔创立的,他认为数学是最容易创造的的一种科学,每个人教应该按照自己的特点重新创造数学知识,每个人有不同的“数学现实”,因而可达到不同的水平。作为每一个教育工作者都知道,通过自身活动所获得的知识与能力,远比别人强加的要理解得透彻,掌握得牢固。正如华盛顿儿童博物馆墙上那句醒目的格言所说:“我听见了就忘记了,我看了就记住了,我做了就理解了。”
一、抛砖引玉,妙用冲突激发学生再创造动机
现代心理学认为,人的一切行为都是由动机引起的,而人的动机、欲望是在一定的情境中诱发的。因此,教学中,教师首先要为学生设置新奇、困惑、充满情趣的教学情境,让学生产生再创造的动机。可从以下几方面着手:
(一)借助游戏、情境激发
教学的艺术不在于传授,而在于激励、唤醒和鼓舞学生的心灵。在数学教学中,适时地给学生营造一个故事或游戏的情境,不仅可以吸引学生的注意力,而且有利于学生发现问题,探索新知。如为在教学《圆柱的体积》时,首先让学生讲“曹冲称象的故事,使学生懂得要用转化的思想来解决问题。然后,想到要想求圆柱的体积,要先把圆柱体转化成长方体,从而推导出圆柱的体积公式。这样,从熟悉的故事入手,有利于学生在情景中发现问题,学习新知。
(二)运用“数学现实”激发
每个学生都有自己生活、学习和思考着的特定的客观世界,以及反映这个客观世界的各种数学概念,它的运算方法、规律和有关的数学知识结构。这就是说,每个学生都有自己的一套“数学现实”,采取相应的方法予以丰富,予以扩展,才能收到实效。例如:通过温度计引进正负数;根据学生的座位安排介绍确定位置;学习了用割补法推导平行四边形面积公式和用双拼法推导三角形面积公式,再放手让学生来推导梯形面积公式,学生自然乐意去再创造,从而实现有效教学。
(三)制造认知冲突激发
如在“年、月、日”的教学中,教师在上课伊始提出这样一些问题:“同学们,你们知道楼老师今年多少岁吗?楼老师的父亲今年五十几岁了,你们今年几岁?过了几个生日?”“楼老师的父亲比你们大得多,可他老人家生日却没你们过得多,你知道这是为什么吗?”教师以现实生活中的一个特殊情况,创设了与一年一个生日的生活经验不相符合的问题,造成了学生认知的不平衡,使学生产生了一种知识上的缺陷感,唤起了学生探索和研究的欲望。
同时,要积极构建宽松、民主、和谐的创造氛围,最大限度地调动学生创造的积极性、主动性。
二、放手探索,巧借支架激活学生再创造潜能
所谓自主探索,就是让每个学生根据自己的体验,用自己的思维方式自由地、开放地去探索,去发现,去再创造。上课时,教师要尽可能将学生放到具体的、形象的情境中去,让他们直观地学习,自由地探索。
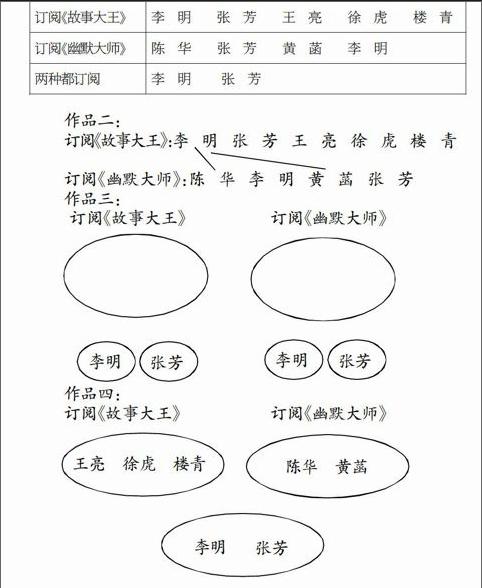
例如:在教学《重叠问题》一课中,教师出示例题:三(1)班订阅《故事大王》的有李明、张芳、王亮、徐虎、楼青5人,订阅《幽默大师》的有陈华、张芳、黄菡、李明4人,问订阅《故事大王》和《幽默大师》一共有多少人?有的学生说9人,有的学生说7人,因为有两人两样都订的。教师跟着追问:从题目中一下子看出有两人都订有些困难,你能设计一个让大家一看就明白的方案吗?等学生设计好后,挑有代表性的作品一一展示,进行表扬,再让学生讨论每一种方法,哪种更优。
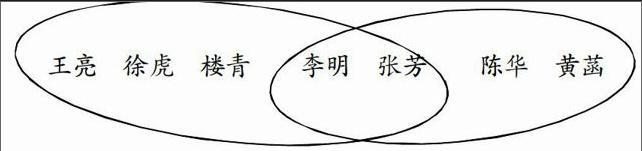
当分析到作品四的时候,有学生说:“这个图没有把订阅《故事大王》和订阅《幽默大师》单独圈出来,上两个圈里是只订这种杂志的。”教师紧跟一句:“那你有什么办法呢?”最后,通过大家的讨论,得出作品五:
韦恩图的雏形就出来了。所以,学生的潜能无限,一定要给他们时间和空间,发挥学生主体的作用,让学生 重走一回数学家们的路。
三、立足猜想,运用推理培养学生再创造能力
数学中的创造都是从猜想开始的。在数学“再创造”过程中,猜想有着同样重要的作用。波利亚认为:只要数学的学习过程稍能反映出数学的发明过程的话,那么就应当让猜想占有适当的位置。
例如:在教《圆的周长》一课时,让学生用滚动法、线绕法、折叠法等多种方法量出圆的周长后,有学生提出:“我觉得这样量圆的周长很麻烦,不精确,有的圆无法量。”
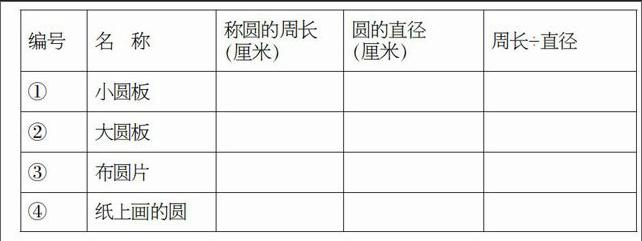
教师:“是啊,如果圆的周长也像正方形、长方形的周长一样,有一个简单的计算方法那该多好啊!我们一起先考虑周长和什么有关?”学生猜测以后,课件演示,得出圆周长和直径有关,直径长的圆周长长,直径短的圆周长短。教师又说:“圆周长和直径到底有什么关系呢?我们知道,正方形的周长正好是边长的4倍,长方形的周长正好是长与宽和的2倍。假如圆周长也正好是直径的几倍,那问题不就解决了吗!现在我们再次小组合作,把刚才量出周长的圆的直径也量出来,记下,然后算一算你量的圆的周长是直径的几倍(保留二位小数),完成《圆的周长研究报告》。”
接着小组活动,汇报交流:初步得出 “圆周长÷直径=3倍多一点”。
再进行验证:
(1) 用3个直径去比周长,发现周长比3个直径稍长一点。
(2)从右图比较得出,圆周长比直径的3倍稍大一点,比直径的4倍小得多。
然后小结:圆周长总是这个圆直径的“3倍多一点”,而且是固定不变的。我们将这个固定不变的倍数叫做圆周率,用字母π表示。
再介绍祖冲之和圆周率。让学生体会数学家的发现与我们的探索是如此的相似!
最后教师再问:“有了圆周率,我们怎样计算圆的周长?”这是时候,学生回答就水到渠成(板书周长公式:圆周长=直径×圆周率,即C=πd。)
面对纸上的圆不易直接测量周长这一问题,学生又自然转入探索周长与直径关系的研究,整个活动充满着挑战。教师为学生提供了充分的从事数学活动和交流的机会,学生则在自主探索的过程中真正理解和掌握了数学知识、数学思想和方法,亲身经历了“圆的周长”计算公式的形成过程,重新体会了创造数学知识的情感,受到了一次生动具体的再创造的训练。
让学生经历数学的“再创造”是我们的责任,作为一名小学数学教师,也许我们无法把学生送到知识的彼岸,但我们可以送他们一叶小舟,在知识的海洋中任意遨游;也许我们无法送学生到达知识的顶峰,但我们可指给他们上山之路,让他们在通往知识的道路上勇于攀登;也许我们无法送学生以智慧,但我们可教给他们学习的方法,用手中的钥匙去开启智慧的大门……

