基于过采样的高精度宽动态范围次声信号采集系统

李鸿征，赵 锋

(焦作大学机电工程学院，河南焦作 454000)

0 引言

次声波是频率小于20 Hz的声波，其不易被水或空气吸收、也不易衰减［1］。在长期的应用中发现次声波和地震存在明显的联系，即次声波异常可以用于对地震进行预测。为了更好地应用于实践中，首先要对信号特性进行深入的分析［2］。故能够完整地还原次声传感器的采样输出信号是次声数据采集系统的核心任务，而其精度也决定了地震预报的准确度。

目前，数据采集系统主要采用先放大再滤波，最后采样量化的方式，当系统要求分辨率很高时，基于传统的方法会遇到奈奎斯特抽样速率的瓶颈问题，因为AD转换器的速度往往限制了系统的速度［3－5］。过采样技术则可以实现传统ADC无法实现的精度，其已成为中低速、高精度AD转换的常用技术，应用于诸多领域［6］。但过采样技术的使用是有一定要求的，即被采样信号的振幅需要和ADC的输入范围接近，本文研究的次声电信号为mV量级的低频信号，幅值相对稳定。由于直接使用过采样技术是无法提高转换精度的［7］，所以，首先对次声信号中的微弱信号进行放大，然后在完成采集过程。

本文利用STM32F103型单片机完成次声信号的数据采集，通过过采样技术以及可编程增益放大器AD8253动态调整增益的能力完成采样，最终完成了次声信号采集系统，从而克服了由于信号幅值过低而导致的过采样失效问题，也提高了系统的采样精度。

1 基本原理

1.1 过采样技术原理及精度提高方法分析

根据奈奎斯特定理［8］，当采样频率为fs时，可将fs一半以内的有效信号重建。其中，小于fs/2的频率的噪声会被混叠在输入信号中。采用数学手段，以白噪声的数学模型近似地描述实际噪声时，信号频带内的噪声能量谱密度有

式中:erms为噪声的平均功率;fs为采样频率;E(f)为能量谱密度。

由于ADC会舍入到最近的量化水平或ADC码值，所以两个相邻ADC码值之间的距离反映了量化误差的大小，故量化电平有

式中:N为AD转换器的位深;Vref为参考电压。

则对应的量化误差eq有

设噪声近似看作为白噪声，而噪声的随机变量在ADC码值之间的分布为零均值。则方差就是平均噪声的功率，有

采样频率和奈奎斯特频率之间的关系可以通过过采样率(OSR)来表示，有

式中fm为输入信号的最高频率。

系统输出端对应的白噪声功率有

通过式(6)可知，增大OSR可减小系统中噪声的功率。由于过采样并不影响信号的功率，所以过采样在减小噪声功率且不影响信号功率的条件下实现了信噪比的提高。

在实际应用过程中，在增加p位精度时，采样频率应至少为

式中:fos为过采样频率;fs为初始采样频率。

通过4p过采样率获得的采样值需求和、平均等处理后方能得到最后的结果。在采集过程中产生的干扰及在低频段的热噪声等大部分是白噪声，其均值约等于0，所以求和平均法具有较好的去噪效果，可以有效提高系统的信噪比。但当将4p个采样值相加后仅除以4p，那只能起到低通滤波的作用，R位的采样数据经过平均后精度不变，并不能提高精度。所以，首先将4p个采样值进行相加，然后产生一个R+2p位的数值，将该数值进行右移p位，又可得到一个R+p位的数值，至此，这个数值才能实现提高p位精度的效果。

1.2 微弱信号的直接过采样技术

设系统的输入信号为三角波，如图1所示，AD传感器的量化步长为LSB1，当采用过采样技术后的量化步长为LSB2。当ADC对其进行采样时，由于ADC的量化步长LSB1超过了三角波信号的幅值，所以其采样值均为0，故不能捕捉原信号的特征。当ADC采用过采样技术后，其采样值分布发生了改变，对应的量化步长变成LSB2，则其采样值不再全是0，可以反映出原始信号的一定的特征。当过采样率足够大时，ADC可以将原有信号可以被分辨。

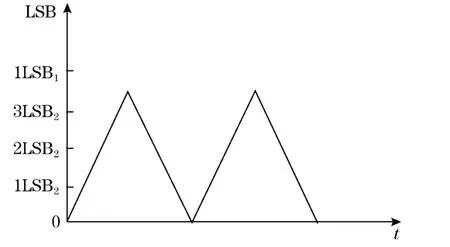
图1 微弱信号的直接过采样分析

如果输入信号值小于ADC的量化步长，则即使过采样率再高，其采样结果也全部为0，无法反映原始信号的特征。这样属于过采样失效。所以，当输入次声信号为微弱信号时，则要先对原始信号进行放大，再进行过采样，最后通过过采样数据实现对ADC分辨率的提高。

2 次声信号采集系统设计

次声电信号大都是低频信号，并且振幅基本在mV量级上，而异常信号时最大振幅为10V，其采集范围大且夹杂有环境噪声。为了保证次声信号的完整性，从而保证对地震预测的准确性。针对被测次声电信号的特点，设计了次声信号采集系统，如图2所示。

图2 次声信号采集系统设计框图

系统采用AD8253(自动调节量程可编程增益仪表放大器)调制ADC前端的信号。经过系统的处理，可以根据输入信号自动地切换模拟输入增益，而不会影响系统的总体性能，为了实时测量出次声电信号的小、大信号的输入，且不必等候系统的建立时间以及因延迟而产生的毛刺。

系统通过阀值来实现动态调整系统增益的功能，阀值的选择对最大化系统的模拟输入范围很重要，可确保在尽可能大的信号范围内使用G=100(G表示增益)模式，同时防止ADC输入过驱。本系统选择500和50000作为阀值。

在G=1时，使用0、500这两个阀值，如果上次ADC转换结果介于0～500之间，增益便切换到G=100模式，这样可确保ADC的模拟输入电压尽可能最大化。

在G=100时，使用50 000、65 535这两个阀值，如果上次ADC转换结果介于50 000～65 535之间，预测下次采样结果，增益切换到G=1模式，以防止ADC超量程。所以，本系统在输入信号在0～(3.3×500÷65535)=0.025 2 V 之间时，放大信号100倍后输入到ADC。

本系统的过采样部分软件设计基本流程为:(1)AD7610以上位机软件设定采样频率的256倍进行采样;(2)每采样256个数据进行一次求和，然后右移4位，作为最终的过采样结果;(3)将过采样结果通过串口上传至上位机，上位机将接受到的数据处理后作为最终结果进行显示和存储。

3 实验

3.1 实验条件

系统选用的ADC是一款16位电荷再分配逐次逼近型寄存器(SAR)架构的模数转换器AD7610。采样频率是上位机软件设定采样频率的256倍，按每提高4倍采样频率能提高一位分辨率来计算，ADC能提高4位分辨率，则最后能达到20位分辨率，完全满足对于次声信号1mV变化的检测。输入的次声信号通过AD7610过采样并进行模数转化，得到的采样值经单片机处理后上传到上位机。STM32作为数据采集系统的核心微控制器，接收上位机关于采样频率的命令，对整体系统的时钟进行控制，主要包括对AD7610采样时钟的控制。

3.2 实验结果分析

本文通过两种方法检测次声信号来比较测量结果:方法1直接以1 Hz的速率采样;方法2利用本系统以1 Hz的速率采样。实验结果如图3和图4所示。

图3和图4分别给出了两种方法得到的次声信号波形。相比直接采样的信号而言，图4中的信号细节部分更明显，在原有的信号基础上引入了0.1 V左右的细节信息。很明显，使用本次声信号采集系统采集到的次声信号对细节的还原度更高，精度也更高。

图3 利用方法1采集的次声信号波形图

图4 利用方法2采集的次声信号波形图

4 结论

本文通过可编程放大器动态调节增益，克服了对于微弱次声信号过采样失效的缺点，采用ADC结合过采样技术，成功地提高了系统分辨率，实现了对次声电信号高精度的采集。由于过采样算法简单，可以通过系统的数字处理能力巧妙实现，相对于传统的采集系统，本采集系统更加经济可靠。在实际应用中，本系统可以满足目前对次声信号研究的需求，具有很高的应用前景。

［1］张新刚，王泽忠.基于过采样技术提高数据采集精度的新方法.电力系统自动化，2004，28(14):58 －62.

［2］李刚，张丽君，林凌，等.利用过采样技术提高ADC测量微弱信号时的分辨率.纳米技术与精密工程，2009，7(1):71－75

［3］吴家平，沈建华.基于STM32微控制器的过采样技术研究与实现.计算机技术与发展，2010，20(2):209 －212.

［4］李刚，张丽君，林凌，等.基于过采样技术的生物电信号检测.电子学报，2008，36(7):1465 －1467.

［5］林琳，杨亦春.大气中一种低频次声波观测研究.声学学报，2010，35(2):200－207.

［6］ABDULLAH MARDINA，HAL J.STRANGEWAYS，DAVID M.A.Walsh.Effects of ionospheric horizontal gradients on differential GPS.Acta Geophysica，2007，55(4):509 －523.

［7］阮双喜.基于ARM的气象数据采集系统的研制.吉林大学学报，2006，24(2):222 －223.

［8］MAZZAFERRI J，LEDESMA S.Wavelet Coefficients Thresholding Method Applied to the Correlation of Noisy Scenes.Processing of SPIE，2004，5622:617 －621.