运用“三法”巧解数学问题
陆晓兰
解决问题作为综合与实践的重要组成部分,在小学数学知识结构中占举足轻重的地位。它是以一类问题为载体、以学生自主参与为主的学习活动。在教师的适当指导下,学生能够在面对问题时,有效整合自己已有的知识、技能和经验,并通过合理的运用和转化,达到未知目标的过程,在这一过程中,学生的情感、态度、价值观均得到了发展,数学的意识和创造性思维也有所提高。本文就小学阶段的几道典型数学问题进行探讨,以此展示如何创新性巧解问题,希望对一线的教师有所帮助。
一、运用“假设法”巧答定义问题
假设法是数学解题的重要方法之一。通过假设可以使复杂的问题简单化,使所求的问题明朗化,帮助学生很快地找到解决问题的突破口,从而使问题化难为易。
在小学数学教学中,笔者发现学生在学习除法时,容易产生这样一个疑问:“为什么在数学运算的过程中,0不能作除数?如果现在回过头来看乘法和除法,它们之间存在着一个互为逆运算的关系。即若有a×b=c,则有c÷a=b(a≠0)。现在假设a=0时也成立,此时有:
当a×1=0,则0÷a=1;
当a×2=0,则0÷a=2;
当a×3=0,则0÷a=3;
当a×4=0,则0÷a=4;
当a×n=0,则0÷a=n(n为非零自然数)。
显然,当a×n=0无限进行下去时,此时0÷a的商不唯一,这就与商的唯一性相矛盾。这就解释了为什么0不能作除数的原因。像数学中的很多重要的定理、定义,都可以采用“假设法”的方式,向学生解释其逻辑性和严密性,从而让学生知其然,也知其所以然。
二、运用“作图法”巧解土地问题
作图法是把应用题的数量关系表示出来,使题意形象具体,一目了然,以便较快地找到解决问题的途径,它对解答条件隐蔽、复杂疑难的应用题,能起到化难为易的作用。
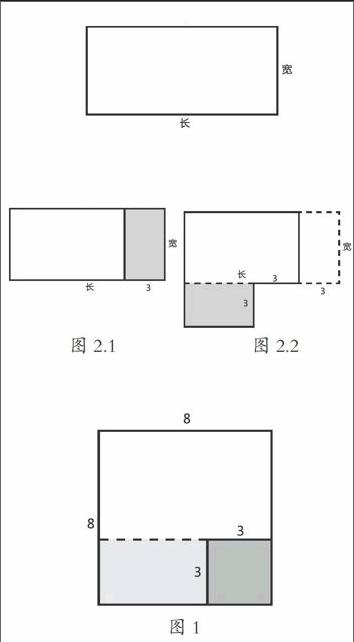
笔者在数学教学过程中,遇到了这样一个问题:有一块长方形菜地,面积为55平方米。长比宽多6米。问长和宽分别有多少米?显然,对于此类问题,以小学阶段的数学知识,是无法解决这一问题。但在古巴比伦的数学中,就涉及了通过作图来解决这一二元一次方程问题:
第一步:按照要求画一个长比宽多6米的长方形(如图1);
第四步:重组的正方形面积为55+9=64(平方米),故边长为8米。因此原来长方形的长为8+3=11(米),宽为8-3=5(米)。
通过作图,这道题目立马显得简单明了,可见作图法的作用非常强大。由于小学生正处在直观形象思维阶段,将抽象的数学与直观的图形巧妙的结合在一起,能够让学生更直观地发现数量关系,这不仅有利于提高学生的学习兴趣,激发学生的思维,同时也开阔了学生的解题的思路,提高解题能力。
三、运用“转化法”巧解生活问题
转化法指将未解决的或待解决的问题,通过某种途径转化为已解决的或易解决的问题,最终使原问题获得解决的一种方法原则。笔者在教学苏教版四年级数学上册《整数四则混合运算》中的“求两积之和(差)的实际问题”时,设计了这样一道题:一个旅游团去公园游玩,成人18人,儿童14人。成人票每张25元,儿童票半价,旅游团购买门票应付多少元?
本题通常的做法是先明确数量关系:成人总票价+儿童总票价=应付的钱,根据条件分别表示出成人总票价和儿童总票价两个量即可解答。成人票总价是25×18,但儿童票的单价是以成人票单价的一半出现,那么儿童票单价为25÷2=?显然四年级学生以现有知识是无法解决这个问题,思考顿时陷入了瓶颈。经过几分钟的思考后,学生会发现有以下几种解决方案:
①把25元化成了250角后再求儿童票单价;
②儿童票是成人票价的一半,故可以把14个儿童转化看作7个成人。即可以列算式25×(18+14÷2);
③先把14个儿童看成14个成人,求出票价后再除以2就得到14个儿童的票价了,算式是18×25+14×25÷2。
通过运用转化的方法,将未知的转化为已知,并以一题多解的形式,既可以让学生在多种解法中比较,从中选出最快最好的解法,同时也给了学生今后解题时探寻最优化解题方法做了深透。经常组织学生进行这样的训练,有利于学生自主建构知识之间的联系,发展学生在解题时的思维敏捷性创造,培养学生的发散性思维能力,鼓励学生积极主动地参与到数学活动中去,让他们觉得数学简单有趣。
以上的三类解决问题的方法,是笔者在数学教学学习过程中所接触到的。在解题的过程中,由于学生已储备了相关的知识经验,形成了一定程度上的思维惯性。当学生在调用原有经验来解决新问题时,发现在计算上出现问题,使得原有的知识系统受到干扰,一时间如果他们无法独立对新、旧知识进行沟通和整合,就会出现对问题质疑的现象。此时,教师必须就要学会对学生在课堂中发出的声音“把脉”,做到适时地介入与科学地处置,从而开启学生思维的盲点,“焊接”学生思维的断层,有效克服学生的思维惯性,从而提升学生创新能力和解决问题的能力[1]。合理恰当地运用上述方法和技巧来解决数学问题,可以收到良好的效果。
【作者单位: 昆山市陆家中心小学校 江苏】

