响应面法在试验设计与优化中的应用

李 莉， 张 赛， 何 强， 胡学斌

(重庆大学三峡库区生态环境教育部重点实验室，重庆 400045)

0 引言

响应面法(Response Surface Methodology，RSM)是由Box等提出的一种试验设计方法［1］，是一种综合试验设计和数学建模的优化方法，通过对具有代表性的局部各点进行试验，回归拟合全局范围内因素与结果间的函数关系，并且取得各因素最优水平值［2］。最初用于物理试验的拟合，近年来已成为国际上新发展的一种优化理论方法，广泛应用于化工、农业、制药、环境和机械工程等领域，国内外许多学者和研究人员对此进行了大量研究［3-7］。与目前广泛使用的正交试验设计法相比较，正交试验不能在指定的整个区域获得试验因素和响应目标之间的明确函数表达式，从而无法获得设计变量的最优组合和响应目标的最优值。而且当试验因素具有较多水平数时，采用正交设计方法仍然需要做大量的试验，实施起来比较困难。响应面法具有试验次数少、试验周期短、精密度高、求得回归方程精度高、预测性能好，能研究几种因素间交互作用等优点［8］，目前已在众多领域得到广泛应用。

1 响应面法的原理及特点

响应面法通过对指定设计空间内的样本点的集合进行有限的试验设计，拟合出输出变量(系统响应)的全局逼近来代替真实响应面。在工程优化设计中，应用响应面法不仅可以得到响应目标与设计变量之间的变化关系，而且可以得到优化方案，即设计变量的最优组合，使目标函数达到最优［9］。

构建响应面近似模型之前应该明确设计变量与分析目标之间的关系，选择合适的函数形式描述当前设计变量与分析目标之间的关系。目前构造响应面的方法主要有多项式、指数函数和对数函数拟合，以及神经网络等近似方法。根据Weierstress多项式最佳逼近定理，许多类型的函数都可以用多项式去逼近，多项式近似模型可以处理相当广泛的非线性问题，因此在实际应用中，不论设计变量和目标函数的关系如何，总可以采用多项式近似模型进行分析［10-12］。

回归模型是用不同阶次的多项式来近似表达响应目标和设计变量之间的关系，具有数学表达式较为简单、计算量小、收敛速度快等特点，并且可以显式表达，是目前研究最深入、应用最广泛的一种方法。

一般地，系统响应Y与设计变量x之间满足:

式中:(x)是未知函数的近似函数，x=［x1，x2，…，xn］为n维独立设计变量;δ为总误差，包含随机误差、建模误差和系统误差等。

如果采用多项式响应面来近似表示系统输入与响应目标两者之间的关系，则有:

式中:φi(x)是基函数;βi是基函数系数;k为基函数φi(x)的个数。

在实际应用中，可根据工程经验确定多项式响应面模型的形式，通常在设计变量的某个范围内采用低阶多项式近似，如用线性函数或二阶模型来拟合。一阶与二阶多项式近似模型的基函数分别为:

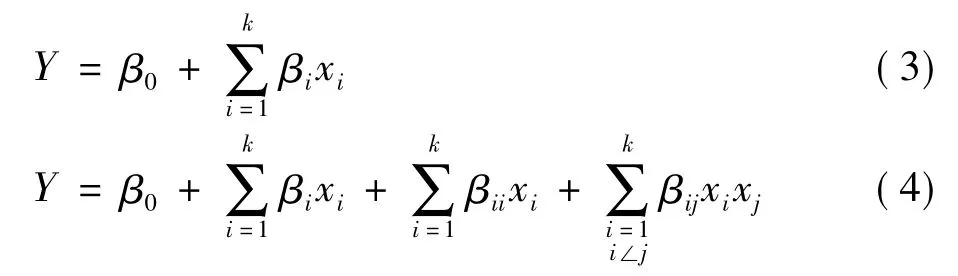
式中:β为未知系数;k为设计变量的数量;Y表示预测响应值;β0、βi、βii分别是偏移项、线性偏移和二阶偏移系数;βij是交互作用系数。

几乎所有的RSM问题都可用以上两个模型中的一个或两个解决。当然，一个多项式模型不可能在自变量的整个空间上都是真实函数关系的合理近似式，但在一个相对小的区域内通常做的很好。最小二乘方法可用来估计近似多项式的参数，然后在拟合曲面上做响应曲面分析。如果拟合曲面是真实响应函数的一个合理的近似式，则拟合曲面的分析就近似地等价于实际系统的分析。如果能恰当地利用试验设计来收集数据，就能够最有效地估计模型参数。

2 响应面法试验设计方法

下面以响应面法优化磷酸铵镁沉淀法(MAP法)去除垃圾渗滤液中的氨氮为例，介绍响应面法利用Design-Expert软件在试验设计与优化中的应用［13］。

2.1 试验因素的选取和单因素最优值范围的确定

确定响应面试验设计因素和水平的方法有多种，常用的方法有:利用已有相关文献结果、单因素试验、爬坡试验、两水平因子设计试验等方法［14-16］。通过相关文献结果、单因素试验确定磷酸铵镁沉淀法去除垃圾渗滤液氨氮的影响因素主要取决于反应pH值、n(Mg)∶n(N)摩尔比、n(P)∶n(N)摩尔比，3 个因素的选取综合考虑氨氮去除效果以及经济因素，取值范围分别为8.0 ～11.0、0.8 ～1.6、0.8 ～1.3。

2.2 响应面试验设计

响应面试验设计方法有多种，较为常用的有Box-Behnken Design(BBD)和Central Composite Design(CCD)。试验设计中实验点分为中心点、立方点和轴向点，示意图见图1。

BBD是响应面优化法常用的试验设计方法，适用于2～5个因素的优化实验。Box-Behnken设计法每个因素取3个水平，以(－1，0，1)编码。其设计表安排以0为中心点，+1，－1分别是立方点相对应的高值和低值。BBD设计的实验点分布情况见图2(以三因素为例)。

CCD有时也称为星点设计。其设计表是在两水平析因设计的立方点基础上加上轴向点和中心点构成的，CCD法每个因素取5个水平，以(0，±1，±α)编码，0为中心点，α为轴向点对应的极值(α=2k/4(k为因素数))。

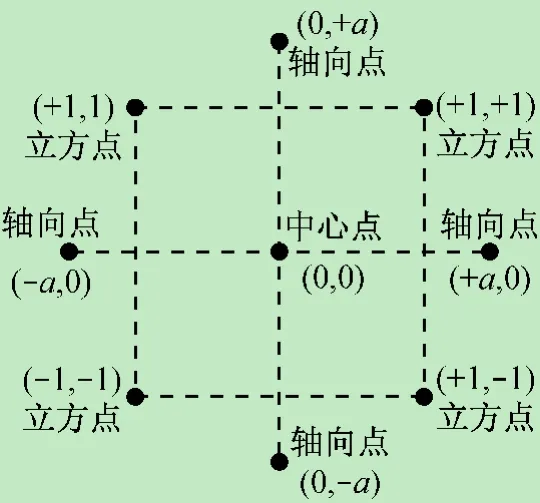
图1 试验设计中的立方点、轴向点、中心点

图2 BBD试验设计实验点分布情况

在因素相同时，由于不存在轴向点，BOXBenhnken设计的试验次数少而更经济，优化求解出的最优工艺水平值不会超出最高值范围，对某些有特殊需要或安全要求的试验尤为适用。根据确定的试验因素和水平。采用 Design-Export软件中的 BOXBenhnken组合设计法确定MAP法去除渗滤液中氨氮的试验设计方案。以各试验单因素最优取值点为中心，上下区域各取1个水平值作为响应面试验设计水平。各设计因素水平值与编码值对应见表1。

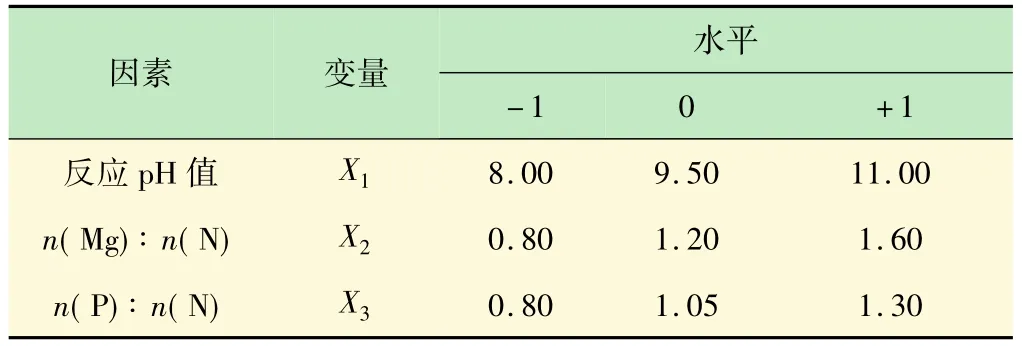
表1 设计因素编码与水平

将各因素及其水平值依次输入系统，则生成试验方案表，见表2，按照该方案进行试验，记录每组因素组合的试验结果，并将试验结果填入对应列。

2.3 构建模型及检验

采用Design-Expert软件对试验结果进行分析，首先点击Analysis按钮，对线性函数，2FI模型、二阶模型、三阶模型进行显著性检验，并通过对模型显著性检测、失拟项检测、相关性检验的数据进行对比，推荐适合的模型。本试验方案结果推荐采用二阶模型。然后(点击ANOVA按钮)根据选择的模型进行方差分析以及显著性检验。方差分析中会对影响二次方程模型的常数项、一次项、二次项(交互作用项)、平方项(曲面作用)的显著性进行检验，如表3所示。

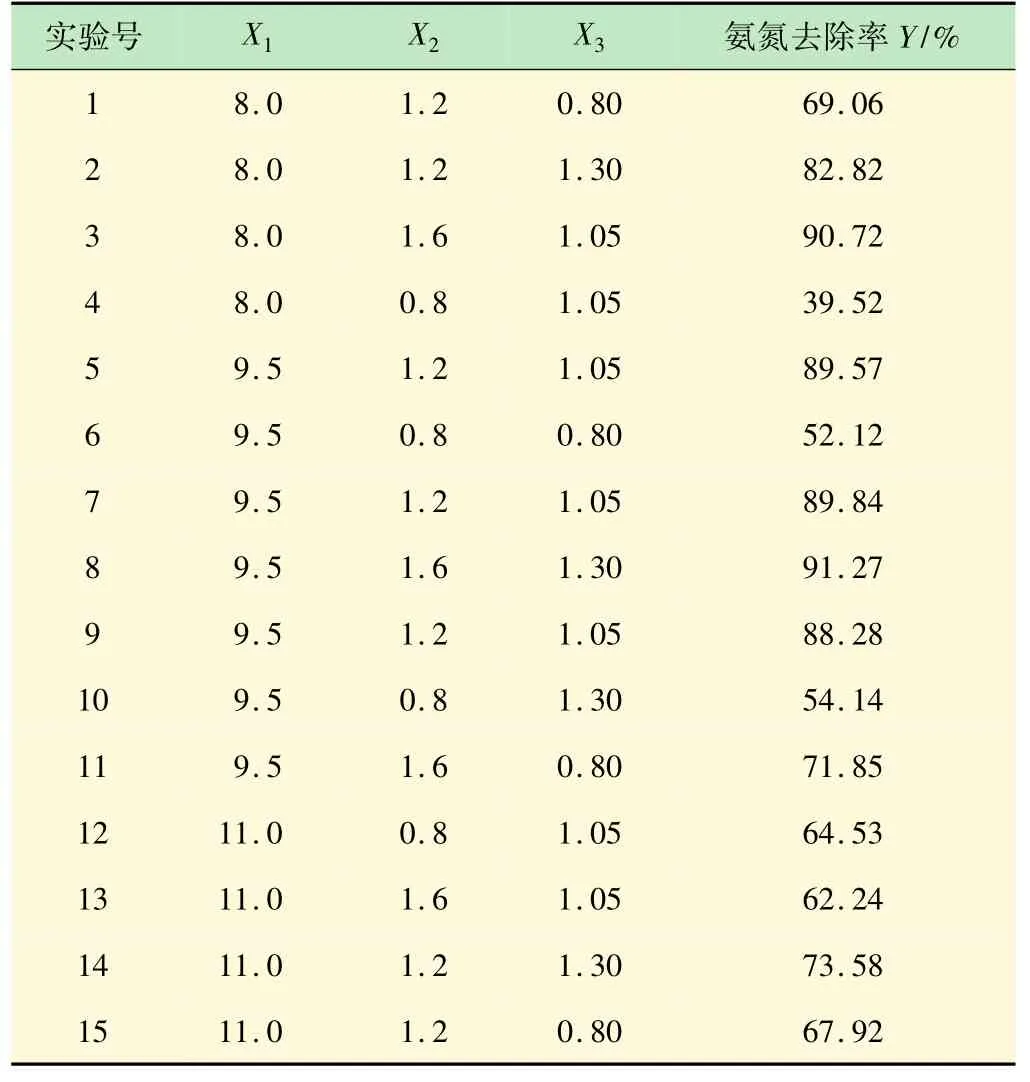
表2 响应面试验设计和结果

表3 回归方程的方差分析表

拟合回归方程为:

进一步对拟合出的回归方程进行误差统计分析，Design-Expert软件对精密度、多元相关系数、可信度、精确度进行了计算，见表4。

大的F值和小的P值代表相关系数的显著性［18］。通过方差分析模型的Pr＞F值＜0.05视为模型是显著的，拟合精度好可以利用该响应面近似模型进行后续的优化设计;失拟项Pr＞F值＞0.05表明不显著，即该模型在被研究的整个回归区域内拟合较好;多元相关系数R2越大，说明相关性越好;Adj R-Squared和Pred R-Squared(RAdj2－RPred2＜0.2)这两个值高且接近，则回归模型能充分说明工艺过程;不高则说明对工艺解释不充分，需考虑是否存在其他显著的影响因子。CV＜10%，表明实验的可信度和精确度高;精密度(Adeq Precision)是有效信号与噪声的比值，大于4视为合理。从表4可以看出，拟合的回归方程符合以上检验原则，适应性较好。

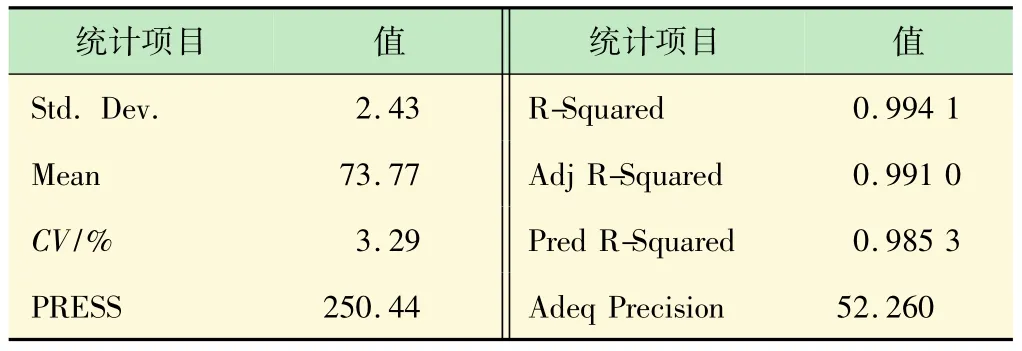
表4 回归方程误差统计分析

Design-Export软件还给出了残差的正态概率分布图、残差与预测值分布图、预测值与实际值分布图。若模型适应性好，则残差的正态概率分布应在一条直线上;残差与预测值分布无规律;残差与预测值分布图尽可能在一条直线上。从图3～5可以看出，利用响应面法拟合MAP法去除渗滤液中氨氮的模型适应性较好。

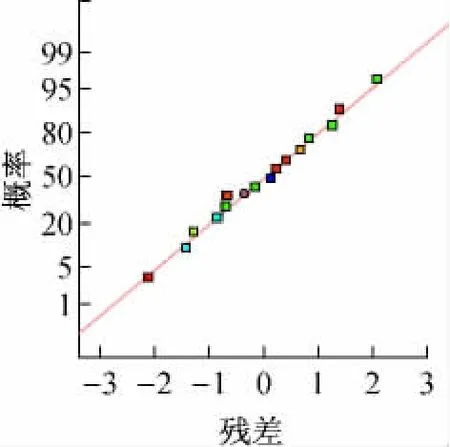
图3 残差的正态概率分布图

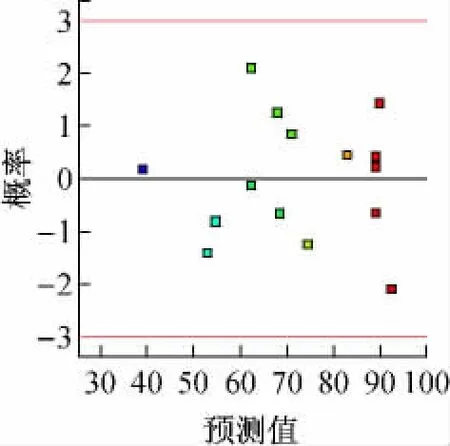
图4 残差与预测值分布图

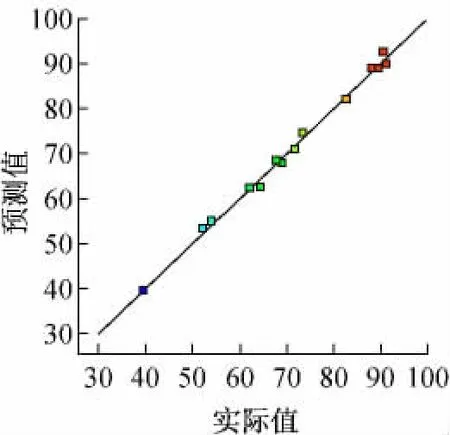
图5 预测值与实际值分布图

2.4 响应曲面和等高线图

响应面法还克服了正交试验不能给出直观图形的缺陷，根据二次方程模型分别做出试验因素间交互作用的三维立体响应曲面和等高线图，考察在某个因素固定在中心值不变的情况下，其他两个因素的交互作用对氨氮去除率的影响，见图6～图8。

图6 n(Mg)∶n(N)和反应pH对氨氮去除率的交互影响

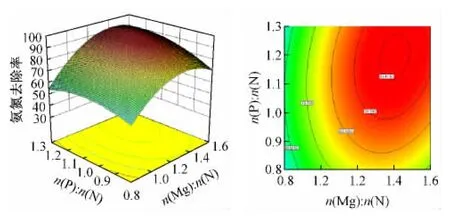
图7 n(P)∶n(N)和n(Mg)∶n(N)对氨氮去除率的交互影响

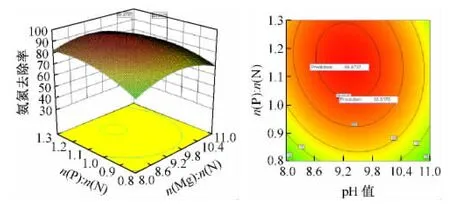
图8 n(P)∶n(N)和反应pH对氨氮去除率的交互影响

等高线的形状为椭圆形表示因素的交互作用显著，圆形则表示交互作用不显著［18］。从图6的等高线图可以直观地看出，pH值与n(Mg)∶n(N)交互作用显著。从三维立体图中可看出，氨氮去除率在合适的反应pH值和n(Mg)∶n(N)摩尔比下，具有最大值，该极大值出现在较低的反应pH值(8.00～8.75)，较高的n(Mg)∶n(N)摩尔比(1.40 ～1.60)范围内。

从图7的等高线图可以看出，在pH值不变条件下，n(Mg)∶n(N)与n(P)∶n(N)摩尔比交互作用显著，三维立体图中可看出，增大n(Mg)∶n(N)与n(P)∶n(N)摩尔比有助于提高氨氮去除率，氨氮去除率存在极大点。该极点出现在n(Mg)∶n(N)摩尔比范围为1.4 ～1.6、n(P)∶n(N) 摩尔比范围为 1.18 ～1.3。

从图8的等高线图可以看出，n(Mg)∶n(N)不变的情况下，pH值与n(P)∶n(N)摩尔比两者交互作用不显著。由三维立体图可见，氨氮去除率存在极大点，pH从8.0提高至8.3时，氨氮去除率增加。当pH继续升高时，氨氮去除率下降，说明氨氮去除率的极点出现在pH为8.4条件下。因两者交互作用不显著，n(P)∶n(N)摩尔比仍应保持在较高的水平1.18～1.30。

3 模型求解及验证

通过对响应面曲线和等高线图进行分析，可以直观看出模型存在极值点，以及对应最佳工艺参数的范围。因此可以采用软件优化功能或者利用二次方程模型分别对参数Xi求导，联解求导所得的方程，即可得到最佳试验条件:X1= －0.81、X2=0.89、X3=0.83，即最佳条件为:pH 8.3，n(Mg)∶n(N)摩尔比 1.55，n(P)∶n(N)摩尔比1.25，此时预测的氨氮去除率响应值为97.94%。

也可以采用软件优化功能，在Design-Expert软件中点击Optimization按钮，然后点击Numerical，在试验因素取值范围内选择响应值最大值(maximum)，可优化最佳条件。在反应过程中不进行酸碱调节，反应pH值可稳定在9.5左右。为了操作方便，控制pH 9.5左右，通过软件优化功能，n(Mg)∶n(N)、n(P)∶n(N)摩尔比最优解分别为1.40，1.19时，氨氮去除率最大响应值为94.03%。

为了检验响应面法的可靠性，一般需要对优化所得的理论最佳条件进行验证。分别选择在pH 8.3，n(Mg)∶n(N)=1.55，n(P) ∶n(N)=1.25;pH 9.5，n(Mg)∶n(N)=1.40，n(P)∶n(N)=1.19 条件下进行三组试验，平均值分别为94.2%、92.2%，与对应条件下氨氮去除率与模型预测值进行对比，相对误差分别约为3.74%、1.83%。说明响应面分析法提供的模型较真实地拟合了实际情况，证明应用响应面法对MAP法去除垃圾渗滤液中氨氮的工艺参数进行优化，不仅科学合理，而且快速有效。

4 结语

响应面法是一种综合试验设计和数学建模的优化方法，可有效减少试验次数，给出直观等高线图和三维立体图，并可考察影响因素之间的交互作用。响应面法不仅建立了预测模型，并对模型适应性、模型和系数显著性和失拟项进行检验，进一步进行方差分析、模型诊断。通过响应面法能有效指导工艺参数的优化，有利于提高生产效益。但是构造能够满足实际工程优化设计的响应面近似模型是一个比较复杂的过程，还需要反复进行试验数据的收集、近似模型的拟合及响应面精度检验。当然，响应面优化法也有其局限性。响应面优化的前提是:设计的实验点应包括最佳的实验条件，如果实验点的选取不当，使用响应面优化法是不能得到很好的优化结果的。因而在使用响应面优化法之前，应当确立合理的实验影响因素与水平。

［1］Box G，Wilson K B.On the experimental attainment of optimum conditions［J］.Journal of the Royal Statistical Society Series B:Statistical Methodology，1951(1):1-45.

［2］Mason R L ，Gunst R F，Hess J L.Statistical design and analysis of experiments with applications to engineering and science［M］.The United States of America:John Wiley and Sons Publication，2003.

［3］Muthukumar V，Rajesh N，Venkatasamy R，et al.Mathematical Modeling for Radial Overcut on Electrical Discharge Machining of Incoloy 800 by Response Surface Methodology［J］. Procedia Materials Science，2014，6:1674-1682.

［4］Ruqayyaha T I D，Jamala P，Alama M Z，et al.Application of response surface methodology for protein enrichment of cassava peel as animal feed by the white-rot fungus Panus tigrinus M609RQY［J］.Food Hydrocolloids，2014，42:298-303.

［5］Yang P，Fang M，Liu Y W.Optimization of a Phase Adjuster in a Thermo-acoustic Stirling Engine Using Response Surface Methodology［J］.Energy Procedia，2014，61:1772-1775.

［6］Wang G J，Wang Y L.Optimization of additives of intumescent fire resistant coating for steel structure by response surface methodology［J］.CIESC Journal，2012，63(3):978-984.

［7］李 莉，张 智，张 赛，等.响应面法优化MAP法处理垃圾渗滤液工艺的研究［J］.环境工程学报，2009，4(6):1289-1295.

［8］秦俊哲，吕嘉枥.食用菌栽培［M］.西安:西北农林科技大学出版社，2002.

［9］周 萍.基于响应面法的车内结构噪声控制研究［D］.长沙:湖南大学，2011.

［10］郭勤涛，张令弥，费庆国.用于确定性计算仿真的响应面法及其试验设计研究［J］.航空学报，2005，26(1):55-61.

［11］王延克，丁渭平，杜飞龙，等.基于响应面法的悬架结构改进及优化设计［J］.机械科学与技术，2009，28(1):10-14.

［12］Ren W X，Chen H B.Finite element model updating in structural dynamics by using the response surface method［J］.Engineering Structures，2010，32:2455-2465.

［13］徐仁崇，刘君秀，曾冲盛，等.采用Design-Expert软件优化透水混凝土配合比设计［J］.新型建筑材料，2010(7):17-20.

［14］顾艳丽，张 慧，刘赛男，等.响应面优化产碱性蛋白酶菌株的产酶条件［J］.大连工业大学学报，2011，30(1):5-9.

［15］欧祖军.部分因析设计的最优折叠反转及相关问题的研究［D］.武汉:华中师范大学，2011.

［16］顾 骏.叶蕊芳，郑 黎.他克莫司发酵培养基的响应面优化设计［J］.工业微生物，2008，38(2):60-63.

［17］Yoshino M，Yao M，Tsuno H，et al.Removal and recovery of phosphate and ammonium as struvite from supernatant in anaerobic digestion［J］.Water Science and Technology，2003，48(2):171-178.

［18］Montgomery D C.Design and Analysis of Experiments［M］.London:John Wiley and Sons Inc，1991.