基于Adams虚拟样机的转向管柱硬点优化设计

胡 伟，曾 志，林成杰

（广州汽车集团股份有限公司汽车工程研究院，广东广州 510640）

0 前言

随着CAE技术的飞速发展，在产品的设计，开发和制造中，虚拟样机技术在解决和改善产品质量，降低开发周期和成本，提高工作效率提供有力支撑。依据设计工作的需要，建立准确的虚拟样机模型，设置合理的设计目标，利用CAE的优化设计手段，实现具体开发工作的优化设计，达到仿真与设计互相促进的目的[1]。

转向管柱硬点由方向盘中心点，上万向节点，下万向节点和小齿轮啮合中心点组成，空间布置的万向节不可避免存在力矩波动[2]，管柱硬点确定涉及到整车的人机工程，周边布置空间，转向器的硬点等约束条件，使用目标分析的方法，通过设定一系列优化参数，提交优化软件计算得出满足条件的结构参数，然后再验证分析，能够大大提高设计效率，并且在保证性能的同时保证约束条件的符合性，本文应用尺寸优化的设计方法，将管柱硬点作为优化参数，得到优化结果后，结合约束条件，并进一步验证、改进设计，最终实现了设计优化目标。

图1 转向管柱模型

1 建立优化模型

1.1 确定设计变量

转向管柱模型示意如图1所示，小齿轮啮合中心点P1和方向盘中心点P4可以作为已知量，其中P1点由底盘硬点决定，P4点由人机硬点决定，产品定型后不能随意变动。寻找合适的空间点上万向节点P3和下万向节点P2，并定义正确的万向节相位角θ，成为转向管柱布置主要课题，为此引入如下矩阵形式的设计变量：

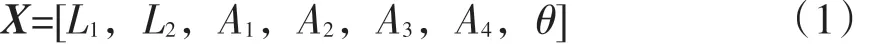
其中L1，L2分别表示P1，P2和P3，P4之间的距离，A1，A2分别表示P1P2和P3P4与Z轴的空间夹角，

A3，A4分别表示P1P2和P3P4在XY平面的投影与X轴的夹角，θ表示上下万向节之间形成的相位角[3]。

定义的已知量和设计变量坐标可以如表1所示。

表1 硬点坐标

1.2 确定目标函数

由于双万向节可等效为单万向节传动，同时万向节传动具有周期性波动的特点，在满足人机和硬点要求的条件下，寻找力矩波动的最小的空间布置，因此定义输出轴和输入轴的角速度的比值与1的差值的最大值定义为力矩波动Wt，并以力矩波动优化的目标函数，设计目标要求小于5%[4]。

其中ω1，ω2为管柱上下两端轴P3P4，P1P2转动角速度

1.3 约束条件

转向管柱的长度，布置角度，相位角由于人机硬点和底盘悬架硬点的限制，取值都在一定的范围之内，结合乘用车车辆的安装布置特点，定义本次优化约束条件如下：

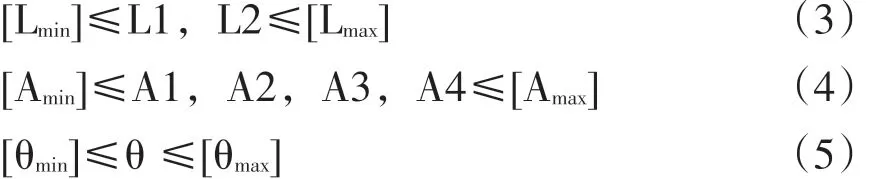
其中[Lmin]，[Lmax]分别为管柱上轴，管柱下轴允许的极限长度，[Amin]，[Amax]分别为管柱上轴，管柱下轴允许的极限空间夹角，[θmin]，[θmax]为上下万向节允许的相位角范围[5]。结合车型的功能需要，设计变量取值范围定义如表2所示。

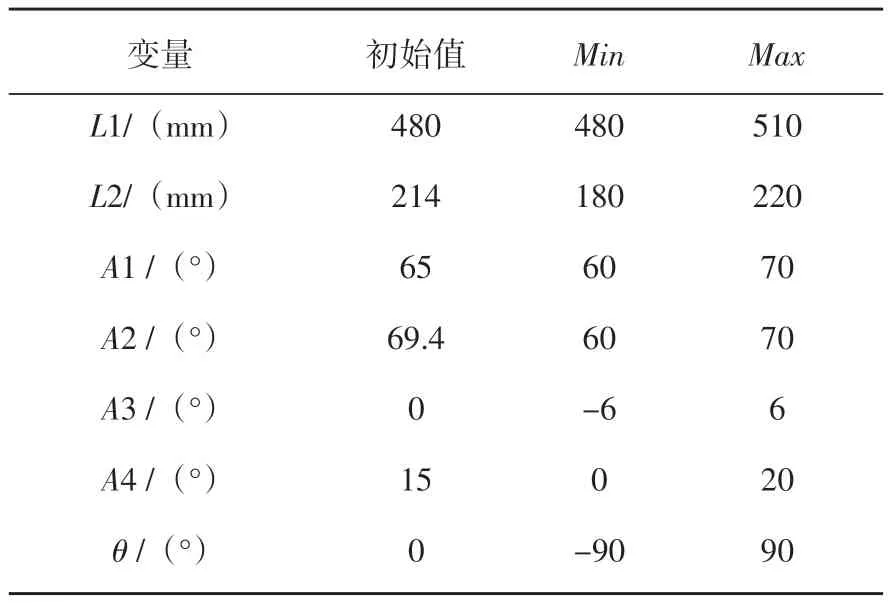
表2 设计变量

1.4 优化数学模型

由式（1）～（5）构造一个具有约束的最优化问题的数学模型[6]。

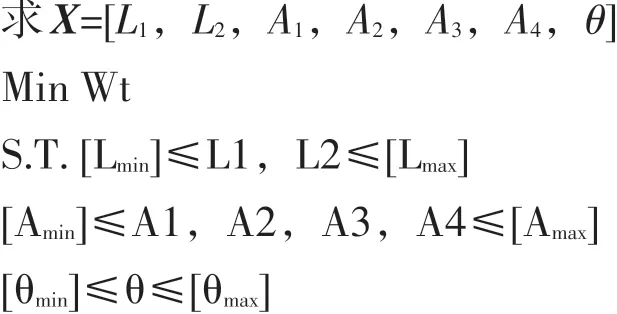
2 波动优化与结果分析

2.1 力矩波动优化流程

Adams是美国MSC公司开发的应用最广泛的机械系统自动化动力学仿真软件。View虚拟样机模块在统一的环境下建立模型、仿真模型和检查结果[7]。

本文采用Adams/View虚拟样机模块，通过目标优化模块进行优化分析。在优化结束之后，还需要将优化后的布置重新进行分析，比较优化前后的尺寸参数是否符合整车布置条件，如果符合则完成优化过程，否则需要将模型和参数等进行再优化[8]。具体的流程如图2所示。

根据1.4提出的数学模型，在View虚拟样机模块中定义设计变量，设计模拟，设计约束和设计目标等优化参数，提交软件进行优化目标的评估。

2.2 优化结果分析

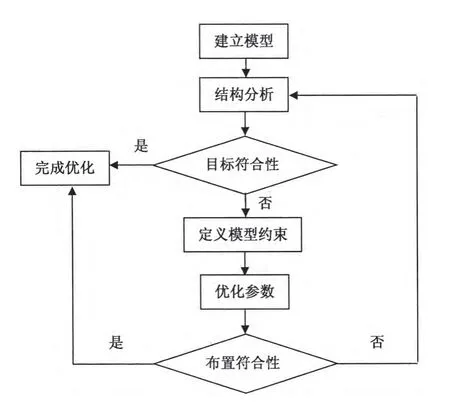
图2 设计优化流程图

根据2.1的优化设计流程，进行尺寸优化分析，得到最终的优化结果，结合设计变量的取值范围并结合产品实际布置情况进行尺寸优化分析。

初始情况下力矩波动分析结果见图3，图4，此时相位角取值为20.13°时，力矩波动为19.6%，不满足设计目标要求。

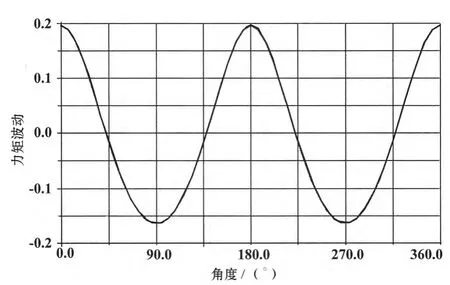
图3 初始Wt值

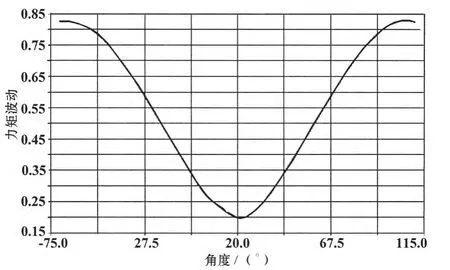
图4 初始Phase_angle

结合约束条件进行优化，通过调整P1P2，P3P4的空间夹角A1，A2，A3，A4来进行角度优化，对长度L1，L2进行尺寸优化，计算结果见图5，图6，当A1=65°，A2=65°，A3=6°，A2=0°，L1=510 mm和L2=180 mm时此时相位角取值为39.36°时，力矩波动为0.5%，满足优化目标要求。

图5 第一次优化数据图

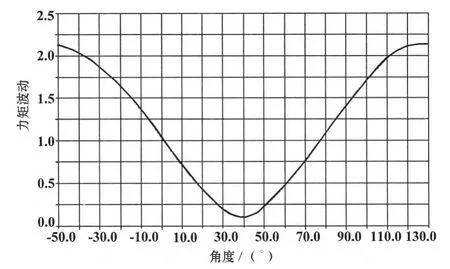
图6 第一次优化Phase_angle

图7 第二次优化数据图

结合优化结果进行实车布置确认，其中A3=6°，A2=0°时转向管柱与周边件有干涉，不满足布置要求，为此在保证布置要求的前提下，并微调P4点坐标为（879，-365，608），计算结果见图7，图8。此时设计变量A1=69°，A2=70°，A3=0°，A2=6°，L1=510 mm和L2=180 mm，相位角取值为84.1°时，力矩波动为1.5%。

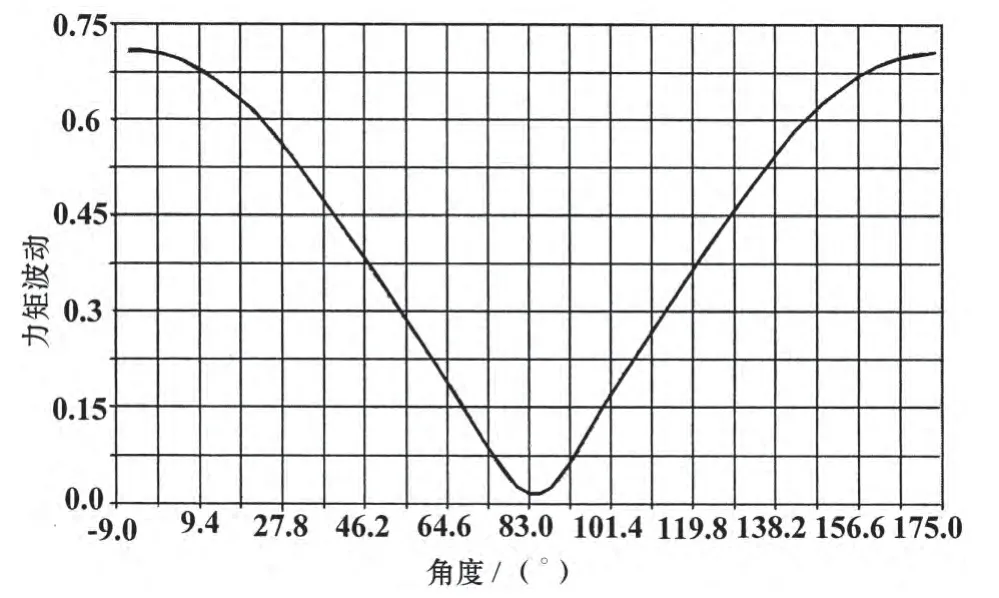
图8 第二次优化Phase_angle

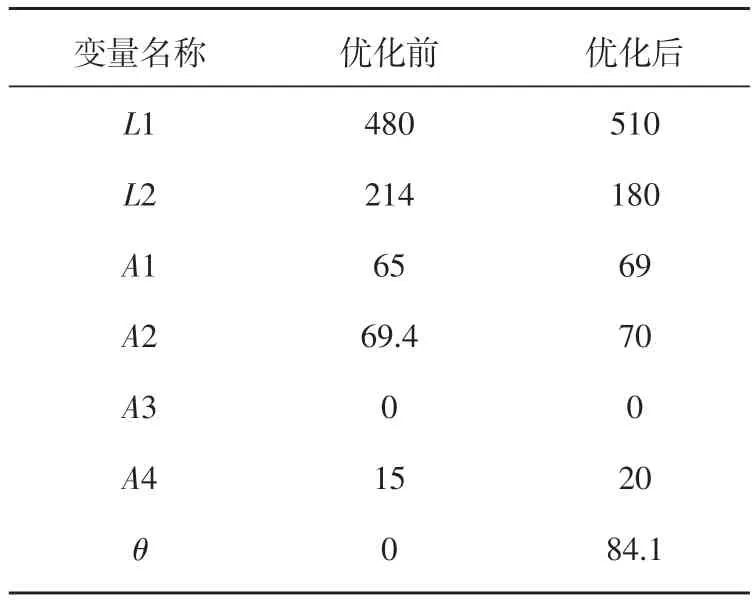
表3 设计变量前后值

经过优化后，最终优化的力矩波动为1.5%，原始布置力矩波动最大值为19.6%，远低于通常5%的目标要求，同时转向管柱硬点满足整车布置要求，设计变量的前后值见表3。

3 结论

（1）本文提出一种转向管柱硬点优化方法，该方法能有效解决转向管柱万向节引起力矩波动问题；

（2）以转向管柱万向节力矩波动作为优化目标，优化的布置参数满足整车布置及力矩波动低于5%的要求；

（3）对整车人机布置和底盘硬点作为已知量，后续会研究人机布置和底盘硬点对波动优化的影响。

［1］郑建荣.adams虚拟样机技术入门与提高［M］.北京：机械工业出版社，2001.

［2］王望予，张建文.汽车设计：4版［M］.北京：机械工业出版社，2008.

［3］潘金坤，罗绍新.汽车转向系统双十字轴式万向节传动优化设计［J］.机械传动，2011（12）：49-52.

［4］林成杰，谷玉川.基于CATIA知识工程对汽车转向系统的力矩波动分析［C］.“广汽丰田杯”广东省汽车行业第七期学术会议论文集，2013.

［5］ 冯振东.空间多万向节传动的转角差和当量夹角的计算［J］.汽车技术，1982（5）：24-30.

［6］刘惟信.机械最优化设计［M］.北京：清华大学出版社，1994.

［7］ADAMS/View Training Guide［Z］.

［8］黄桥，游祥军.基于ADAMS转向系统硬点优化［J］.汽车零部件，2013（12）：47-50.