渐开线齿廓曲线数学模型研究

成建群

（苏州健雄职业技术学院机电工程系，江苏太仓 215411）

1 研究前提

首先说明一下范成法渐开线齿轮(不作特别说明，这里提到的齿轮均是指渐开线齿轮)切削加工。范成法是利用一对齿轮互相啮合传动时其两轮的齿廓互为包络线的原理来加工齿轮的，其刀具和轮坯之间的对滚运动与一对互相啮合的齿轮的运动完全相同，所以这种方法加工的齿轮都能正确的啮合[1]。用这种方法加工时，若刀具的齿顶线或齿顶圆与啮合线的交点超过被切齿轮的极限点，则刀具的齿顶将被切齿轮之齿根的渐开线齿廓切去了一部分，这种现象称为根切现象。如果将根切去的材料补充全，实际应用中齿轮就可能卡死，造成齿轮不能工作。其中刀具的齿顶圆愈平直，愈易超出轮坯的根切极限点，所以齿条刀具最易发生根切现象，同时也就是说，用齿条刀具加工的齿轮不会出现卡死想象[2]。

为了达到减少根切量、调整齿轮中心距、改善齿轮磨损和强度等要求常采用变位齿轮，当变位量为零时，可以认为是标准齿轮[3]。也就是说标准齿轮是变位齿轮的特例。

现对圆柱渐开线齿轮（模数m、压力角a、齿顶高系数ha、齿根高系数hf、齿数z、变位系数x、分度圆齿厚s、齿间宽e），求齿廓曲线。（压力角计算时要转化为弧度）。

不妨首先求出其中一个齿面的轮廓曲线。默认直角坐标系原点为齿轮轴心（不作特别说明，插图中O点均是指这一点）[4]。

2 求解轮廓曲线

2.1 不发生根切时

条件：

其中ha1为刀具的齿顶高系数。显然ha1=hf。

2.1.1 当齿根圆不小于基圆时

参数举例：模数m=1.5、压力角a=20°、齿顶高系数ha=0.8、齿根高系数hf=1.25、齿数z=45、变位系数x=-0.45、分度圆齿厚s=2.356 194 45、齿根倒角半径rfr=0.5、齿顶倒角半径rar=0.5。

此时可以假设齿廓曲线依次有如下几部分组成：齿根圆弧、齿根过度圆弧、渐开线、齿顶圆弧过度、齿顶圆弧。

2.1.1.1 齿根倒角

如图1，设齿根倒角半径为rfr，计算过程如下，

设齿根倒角圆心O(x0，y0)，则∶

结论：

设齿根圆弧（x，y），则0≤t≤a9时，

设倒角圆弧（x，y），则0≤t≤a7时，

设渐开线（x，y）（以压力角为参数建立参数方程、b2由齿顶倒角给出），则a2≤t≤b2时，

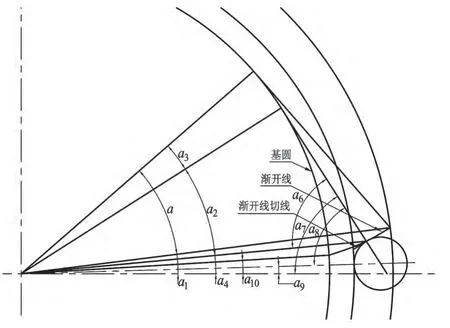
图1 齿根倒角

2.1.1.2 齿顶倒角

如图2，设齿顶倒角半径为rar，计算过程如下，

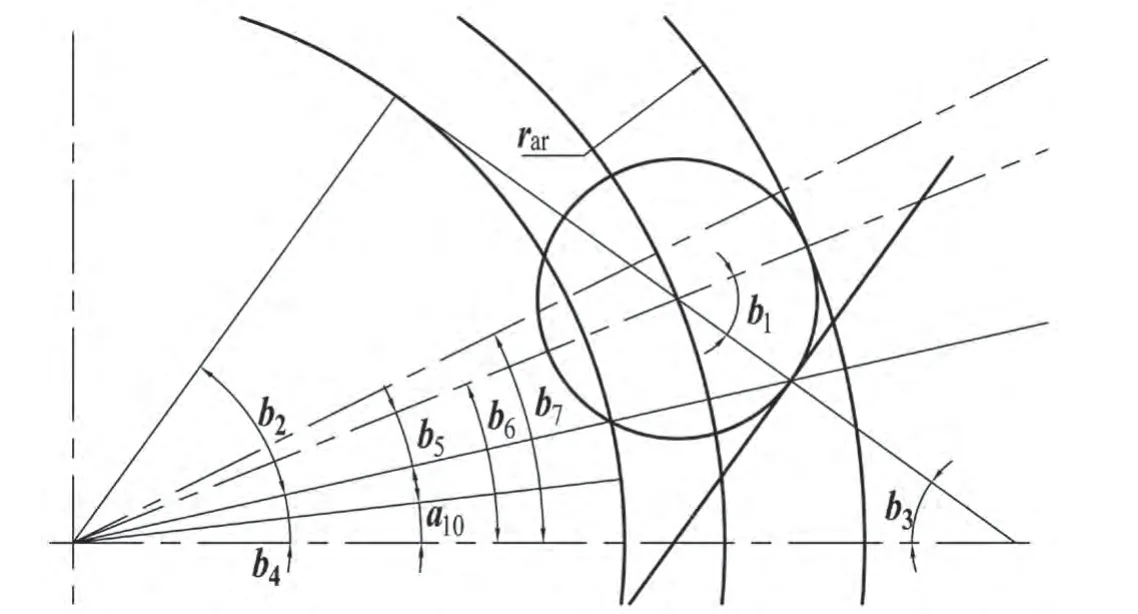
图2 齿顶倒角

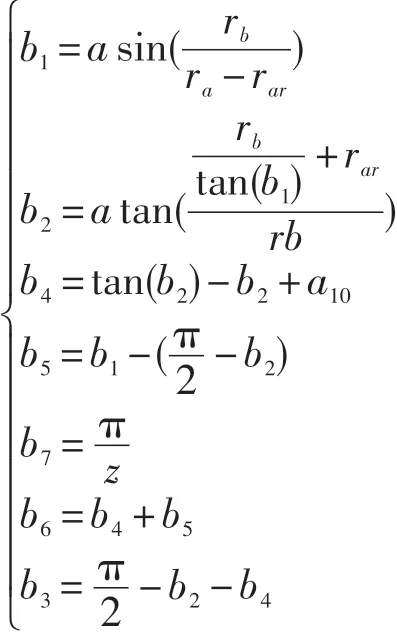
齿顶倒角圆心o(x0，y0)

结论：

设齿顶倒角圆弧（x，y），则0≤t≤b1时，

设齿顶圆弧（x，y），则b6≤t≤b7时，

2.1.2 当齿根圆小于基圆时

条件：

即：

参数举例：模数m=1.5、压力角a=20°、齿顶高系数ha=0.8、齿根高系数hf=1.25、齿数z=27、变位系数x=0、分度圆齿厚s=2.356 194 45、齿根倒角半径rfr=0.5、齿顶倒角半径rar=0.5。

如图3，由于在基圆内没有渐开线，不妨用渐开线起点切线延长渐开线，设齿根依旧有倒角，此时有个临界情况，即倒角刚好切于渐开线起点A，此时倒角半径为rt[5]。

图3 齿根圆小于基圆

不难看出，

可得，

当rt≤rfr时，可以按照基圆小于齿底圆情况处理。

当rfr≤rt时，齿廓曲线依次由如下几部分组成：齿根圆弧、齿根过度圆弧、直线段、渐开线、齿顶圆弧过度、齿顶圆弧，其中齿顶圆弧过度、齿顶圆弧与基圆小于齿底圆情况相同。

计算过程如下，

设o2(x0，y0)，则：

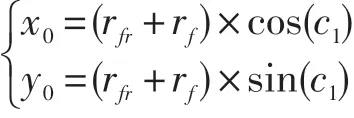
结论：

设齿根圆弧（x，y），则0≤t≤c1时，

设倒角圆弧（x，y），则0≤t≤c3时，

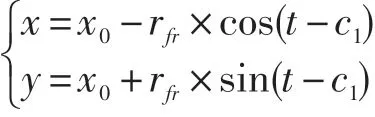
设线段DA，其中D（xD，yD），A(xA，yA)，则，

设渐开线（x，y）(以压力角为参数建立参数方程)，则0≤t≤b2时，

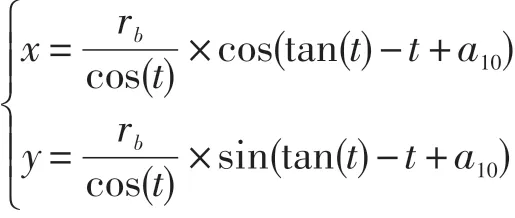
2.2 发生根切时

条件：

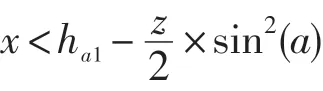
其中ha1为刀具的齿顶高系数。显然ha1=hf。

如图4，啮合点在PB2上移动，N点、N1点分别为不同时刻渐开线的起点，M1点的变化就构成了根切。M1点很显然是从M点开始进入根切，从B2点出根切，设OM1=t，以齿根中轴线OX建立相对坐标系，M点的轨迹就构成了根切曲线。

图4 根切

计算过程如下，

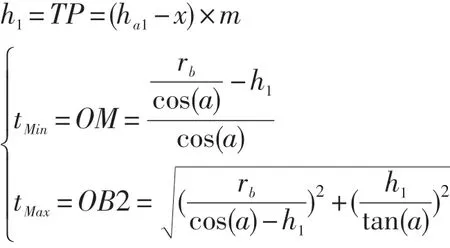
t的范围是[tMin，tMax]

这里不难看出，当发生根切现象时，齿根圆一定小于基圆。（齿根圆由M点决定，基圆由N点决定，当M低于N点时，不会发生根切。）首先不考虑根切问题，按照前面2.1.2当齿根圆小于基圆时的情况产生曲线，然后根据这里的结论产生曲线，比较如图5，粗线部分为根切曲线，B2左边一段细实线为直线，B2右边一段细直线为渐开线[6-7]。

如图6，根切部分（MB2段）在整个齿廓上位置如下：

图5 根切曲线

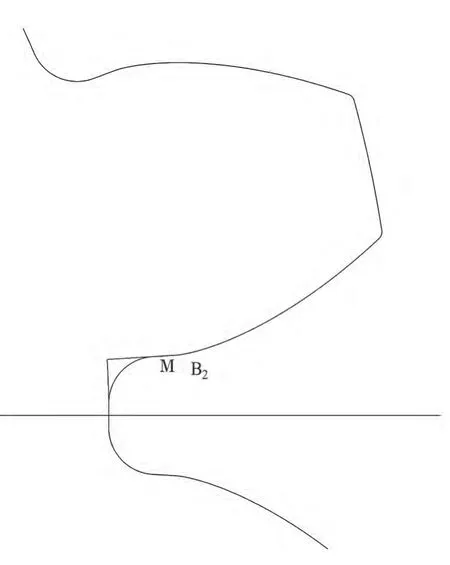
图6 根切位置

为了曲线间平滑过渡，要利用导数方程，计算如下：

根切曲线M1（x，y）

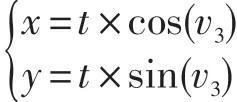
根切曲线斜率：

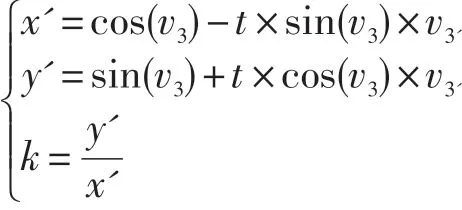
为了简单起见，这里不考虑圆弧过渡。

如图3所示，M点在BA线段上，B2点在由A开始的渐开线上，构成了由B、M、A、B2四点组成D的取值范围：

（1）当D在BM上时，曲线依次为齿根圆弧、齿根倒角、直线段、根切曲线、渐开线、齿顶倒角、齿顶圆弧；

（2）当D在MA上时，曲线依次为齿根圆弧、齿根倒角、根切曲线、渐开线、齿顶倒角、齿顶圆弧；

（3）当D在AB2上时，曲线依次为齿根圆弧、齿根倒角、根切曲线、渐开线、齿顶倒角、齿顶圆弧；

（4）当D在AB2外时，曲线依次为齿根圆弧、齿根倒角、渐开线、齿顶倒角、齿顶圆弧。

为了体现根切特征，进一步简化问题，在后面三种情况下，均认为D点重合于M点。

结论：当D在BM上时，曲线依次为齿根圆弧、齿根倒角、直线段、根切曲线、渐开线、齿顶倒角、齿顶圆弧。

此外，曲线依次为齿根圆弧、齿根倒角、根切曲线、渐开线、齿顶倒角、齿顶圆弧。(其中倒角半径决定于M点，设为rm。)

与求rt的方法一样，可得：

2.2.1 D在BM上时

条件：rfr＜rm

参数举例：模数m=1.5、压力角a=20°、齿顶高系数ha=0.8、齿根高系数hf=1.25、齿数z=15、变位系数x=0.3、分度圆齿厚s=3、齿根倒角半径rfr=0.5、齿顶倒角半径rar=0.1。

曲线依次为齿根圆弧、齿根倒角、直线段、根切曲线、渐开线、齿顶倒角、齿顶圆弧。

结论：

设齿根圆弧（x，y），则0≤t≤c1时，

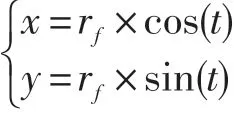
设倒角圆弧（x，y），则0≤t≤c3时，

设线段DM（其中D（xD，yD），M(xM，yM)），则，

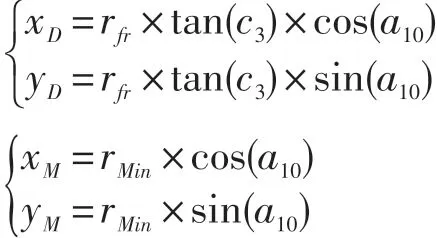
根切曲线如上。

设渐开线（x，y），v5为B2处压力角，则

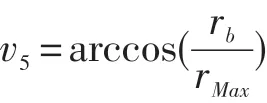
则v5≤t≤b2时，

齿顶倒角、齿顶圆弧曲线和没有根切时一样。

2.2.2 D在BM外时

条件：rfr＞=rm

参数举例：模数m=1.5、压力角a=20°、齿顶高系数ha=0.8、齿根高系数hf=1.25、齿数z=10、变位系数x=0.3、分度圆齿厚s=3、齿根倒角半径rfr=0.8、齿顶倒角半径rar=0.1。

曲线依次为齿根圆弧、齿根倒角、根切曲线、渐开线、齿顶倒角、齿顶圆弧。计算和求c1、c2、c3、o2一样，只是此时令rfr=rm，于是：

设o2（x0，y0），则：

表示如下：

设齿根圆弧（x，y），则0≤t≤c1时，

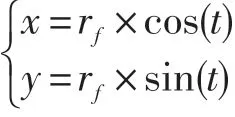
设倒角圆弧（x，y），则0≤t≤c3时，

根切曲线如上。

设渐开线（x，y），v5为B2处压力角，则，

则v5≤t≤b2时，

齿顶倒角、齿顶圆弧曲线和没有根切时一样。

3 参数有效性讨论

对于齿轮参数模数m、压力角a、齿顶高系数ha、齿根高系数hf、齿数z、变位系数x、分度圆齿厚s、齿间宽e，均应该符合实际情况。如x可取正负值，z为正整数，其余为正数，一般而言，模数m=1.5、压力角a=20°、齿顶高系数ha=0.8、齿根高系数hf=1.25、齿数z＞=17、变位系数|x|＜0.5、分度圆齿厚s=2.356 194 45(依赖于变位系数)[8]。

在求各个中间参数时，有的函数对自变量有取值范围的要求，否则求解没有意义，造成模型错误，所以应该适当讨论。如∶

4 结束语

建立渐开线齿廓曲线模型还需要利用曲线对称数学模型、曲线旋转数学模型、三角形外接圆圆心与圆心角数学模型（这些模型相对简单，不用累述）。

可利用Autodesk公司Autolisp编程实现模型结果。对于内齿轮，将会出现顶切的问题而且内齿轮的齿顶圆必须不小于基圆[10]。分别可以表示如下：

数学模型是软件开发的基础，它的正确与否直接关系到软件的正确性。有了渐开线齿廓曲线数学模型，渐开线齿轮的CAD/CAM软件开发易如反掌。它是齿轮CAD/CAM的核心技术。

本模理论上正确，层次清楚，数学形式简单，经过实践检验完全符合渐开线啮合原理。

［1］邹慧君，张春林，李杞仪.机械原理［M］.北京：高等教育出版社，2006.

［2］岳大鑫，王忠.机械设计基础［M］.西安：西安电子科技大学出版社，2008.

［3］邱印辉.机械原理与设计［M］.大连：大连理工大学出版社，2006.

［4］LITVIN F L.Gear geometry and applied theory［M］.N J：Prentice-Hall，1994.

［5］Di Francesco G，MARINIS.Structural analysis o f a sym⁃metrical teeth：reduction of size and weight［J］.Gear Technology，1997，14（5）：47-51.

［6］樊智敏，张汝琦.双渐开线齿轮传动的啮合分析［J］.机械科学与技术，2003，22（5）：779-781.

［7］周志峰，刘伟，王婧.渐开线直齿轮修形的有限元分析与研究［J］.机电工程，2013（12）：1490-1493.

［8］张光辉，许洪斌，龙慧，等.分阶式双渐开线齿轮［J］.机械工程学报，1995，31（6）：47-52.

［9］朱旭辉.基于ADAMS的非对称渐开线齿轮动力学仿真［J］.机电工程技术，2014（8）：107-110.

［10］孙士保.AutoCAD2008中文版应用教程［M］.北京：机械工业出版社，2009.