基于FANUC-0i系统数控铣削非圆曲线零件宏程序的编制

吴 凯，张柳清

（茂名技师学院，广东茂名 525011）

0 引言

在机械制造业中，各类CAD/CAM软件越来越多地应用在数控曲面加工中，CAD/CAM软件中生成刀具路径就是在允许的误差值范围内沿每条路径用直线去逼近曲线曲面的过程，CAD/CAM软件生成的程序庞大无比，占用空间大，对于要求高的精密的曲线轮廓零件，降低了零件的尺寸精度和轮廓形状精度，而对于这些非圆曲线方程类轮廓零件保证其轮廓精度对使用性能至关重要。宏程序编制的程序与CAD/CAM软件生成的程序相比，程序大大简化，输入与调试方便快捷，解决CAD/CAM软件编程计算坐标值繁琐、程序庞大、程序难修改等难点问题。宏程序是手工编程的最高级形式，同时也是手工编程的一个难点，本文结合宏程序编程的特点，通过建立数学模型、列变量处理表、画程序流程图和仿真验证四大步骤快速高效地编制非圆二次曲线零件加工通用的宏程序模板，大大扩展了数控机床的应用范围。

1 FANUC-0i系统用户宏程序简介及其编程特点

1.1 宏程序简介

程序中具有变量、并利用变量进行赋值和表达式来进行逻辑运算的程序称为宏程序。平常所说的宏程序就是用户宏程序。宏程序是数控系统所具有的特殊编程功能，FANUC-0i系统宏程序结构是基于BASIC语言建立的，常用B类宏程序，它借助IF、WHILE语句可以控制宏程序的流向，常用的转移和循环语句有三种[1-2]：

（1）无条件转移指令（GO TO语句）

GO TO目标程序段号

无条件转移指令用于无条件转移到指定程序段号开始执行。

（2）条件转移指令（IF语句）

①IF[条件表达式]GO TO n

当条件满足时，转移到指定程序段，如果条件不满足时则执行下一程序段。

②IF[条件表达式]THEN宏语句

当条件表达式满足时执行预先决定的宏语句。

循环指令（WHILE语句）

WHILE[条件表达式]DO m（m=1，2，3）

‥‥

END m

当条件表达式满足时，就循环执行DO与END之间的程序段，条件表达式不满足时，则执行END后的下一个程序段。

1.2 宏程序编程特点

宏程序中通过对变量进行算术、逻辑和函数运算，应用更灵活、方便。其编程特点如下。

（1）宏程序具有灵活性、通用性和智能性特点[3]。若程序中某数据需要更改，只需将相应变量重新赋值即可，这样使宏程序有着广泛的通用性。

（2）宏程序编程最体现模块化思维[3]。编程人员只需要根据零件几何信息和不同的数学模型可完成相应的模块化加工程序设计。对于相似零件的重复性加工或有规律性地重复一个动作，宏程序只要改变变量的值，即可完成不同的加工或操作。

（3）宏程序逻辑严密，可读性强，占用机床数控系统空间小[3]。宏程序天生短小精悍。一般常见的数控系统完全容纳得下任何复杂的宏程序，数控机床执行宏程序时数控系统的计算机可以直接进行插补运算，而且运算速度极快加工效率高。通俗地说，宏程序就是小程序解决大问题[1]。

（4）宏程序加工精度高[3-4]。CAD/CAM软件编程时，在建模、刀具轨迹生成、后置处理环节都存在一定的误差，在不同建模软件CAD图档转换也会产生一定的精度误差，宏程序可以有效地避免CAD/CAM软件编程产生的误差，加工精度高。

2 非圆二次曲线类零件编程的数学分析

2.1 非圆二次曲线编程数学处理

工程上处理用数学方程描述的平面非圆曲线轮廓图形常采用相互连接的直线逼近法和圆弧逼近法[4]。

（1）直线逼近法。一般来说，由于直线法的插补节点均在曲线轮廓上，容易计算，编程也简便些，所以常用直线法来逼近非圆曲线，其缺点是插补误差较大。

（2）圆弧逼近法。曲线的圆弧逼近有曲率圆法、三点圆周法和相切圆周法等方法，这些方法须先用直线逼近法求各节点再求各圆周，其计算较繁琐。

2.2 编制非圆二次曲线加工宏程序的步骤

宏程序对可以用函数公式描述的工件轮廓或曲面进行数控加工，是现代数控系统的一个重要功能，数控加工公式曲线宏程序编制具有一定的规律性。可按以下步骤进行：（1）建立数学模型，确定自变量和因变量；（2）列变量处理表，通过表格形式，清楚条理地把数学模型表达式转化成宏变量表达式；（3）画流程图，按流程图写出程序；（4）仿真模拟加工验证

3 非圆二次曲线类零件宏程序的编制实例

图1 椭圆宏程序流程图

椭圆零件是典型的非圆二次曲线零件，下面以椭圆零件为例论述此类零件一般宏程序的编制步骤。

例 数控铣削加工图1所示椭圆零件外形轮廓，试编制其加工宏程序（FANUC-0i系统）。

解：分别选择标准方程和参数方程编制该椭圆外轮廓的精加工程序，走刀路线为：A→B→C→D→C→E→A。见图2所示。

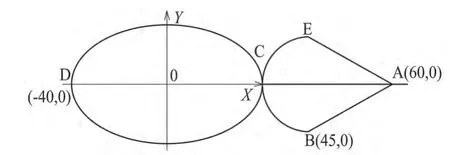
图2 椭圆宏程序流程图

3.1 标准方程加工椭圆

（1）标准方程加工椭圆要建立数学模型，其表达式及曲线变量处理表见表1所示。

表1 标准方程加工椭圆曲线变量处理表[5]

表2 参数方程加工椭圆曲线变量处理表[5]

（2）宏程序如下：

O1018

G54 G00 G90 X60.0 Y0.； 定位到A点。

M03 S1200； 主轴正转。

G01 Z-5.0 F200； 切深5 mm

G42 G01 X45.0 Y-5.0 D01 M08； 右刀补进刀到B点。

G02 X40.0 Y0.0 R5.0； 圆弧切向进刀到C点。

#20=40.0； 椭圆长半轴赋初值。

WHILE[#20GT-40.0]DO1； 当X值大于-40.0时执行循环1。

#20=#20-0.15； X值递减0.15mm。

#21=25.0*SQRT[1-#20*#20/[40.*40.]]；计算第一、二象限的Y坐标值

G01 X#20 Y#21 F150； 直线插补运算逼近椭圆曲线。

END 1； 循环1结束。

WHILE[#20LT40.0]DO2； 当X值小于40.0时执行循环2。

#20=#20+0.15； X值递增0.15 mm。

#21=-25.0*SQRT[1-#20*#20/[40.0*40.0]]；计算第三、四象限的Y坐标值。

G01 X#20 Y#21 F150； 直线插补运算逼近椭圆曲线。

END 2； 循环2结束。

G02 X40.0 Y5.0 R5.0； 圆弧切向退刀到E点。

G00 G40 X60.0 Y0.0 M09；取消右刀补，退刀到A点。

M05； 主轴停。

M30； 程序结束。

3.2 参数方程加工椭圆

（1）首先建立椭圆参数方程的数学模型，其表达式及椭圆曲线变量处理表见表2所示。

（2）画程序流程图

程序流程图是计算机高级语言编程中常用的工具，它全面描述系统逻辑、反映信息在系统中的流动、处理情况。它通过图框形式指示程序流程，控制程序的走向，具有直观易读和易理解的特点，使编程思路清晰、流畅、条理性强，宏程序可借用流程图的形式，编程前先按逻辑顺序画出流程图，然后按流程图就容易编写程序。参数方程编程先根据思路画出流程图，见图3所示。

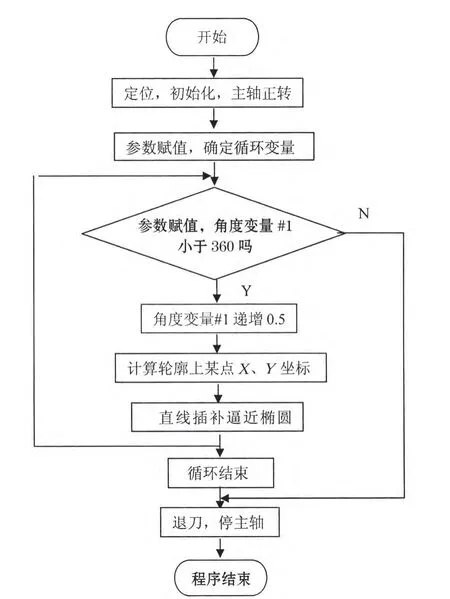
图3 椭圆宏程序流程图

（3）根据流程图写出其加工程序

O1809

G54 G90 G00 X60.0 Y0.0； 定位到A点。

M03 S1200； 主轴正转。

G01 Z-5.0 F200： 切深5mm

G01 G42 X45.0 Y-5.0 DO1 M08； 右刀补进刀到B点。

G02 X40.0 Y0.0 R5.0 F150； 圆弧切向进刀到C点。

#1=0.0； 角度变量赋初值0。

WHILE[#1LE360.0]DO 1； 当#1≤360O时执行循环1。

#1=#1+0.5； 角度变量#1递增0.5O。

#20=40.0*COS[#1]； 计算X坐标值。

#21=25.0*SIN[#1]； 计算Y坐标值。

G01 X#20 Y#21 F150； 直线插补运算逼近椭圆曲线。

END 1； 循环1结束。

G00 G40 X60.0 Y0.0 M09； 取消右刀补，退刀到A点。

M05； 主轴停。

M30； 程序结束。

（4）仿真模拟加工验证

为了验证程序的正确性，避免由于程序的原因对机床造成的损伤，下面用CAXA制造工程师编程助手软件仿真加工过程，CAXA制造工程师编程助手支持自动导入代码和手工编写代码，其中包括宏程序代码的轨迹仿真，能有效验证代码的正确性[6]。

1）打开CAXA制造工程师2008的编程助手，进入软件界面。

2）在程序代码框中录入O1809的宏程序。

3）代码录入完成后，进行仿真加工，选择[仿真]→[加工仿真]，弹出对话框，选择步长5，前进方向选择[前进]，单击[开始]按钮。见图4。

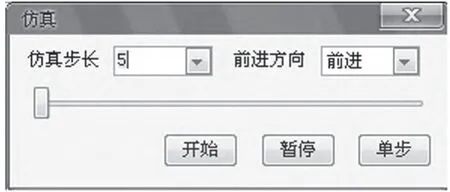
图4 仿真加工对话框

仿真结束图见图5，当宏程序中有代码错误或格式不对时软件会提示，根据提示进行修改。

3.3 模块化程序转化

该例是编制椭圆类零件加工的典型程序。可作为一个编程模板使用，需要时通过调用指令M98或G65等调用，程序中可通过修改自变量#20及椭圆长短半轴参数实现各类不同大小的椭圆零件的加工。另外，通过修改刀具半径D01的值及角度增量值的大小可实现椭圆的粗加工、半精加工、精加工，而其它数据不用改变，增强程序的通用性，大大地缩短了编程周期和工作量，从而提高生产效率和经济利益，起到事半功倍的效果。

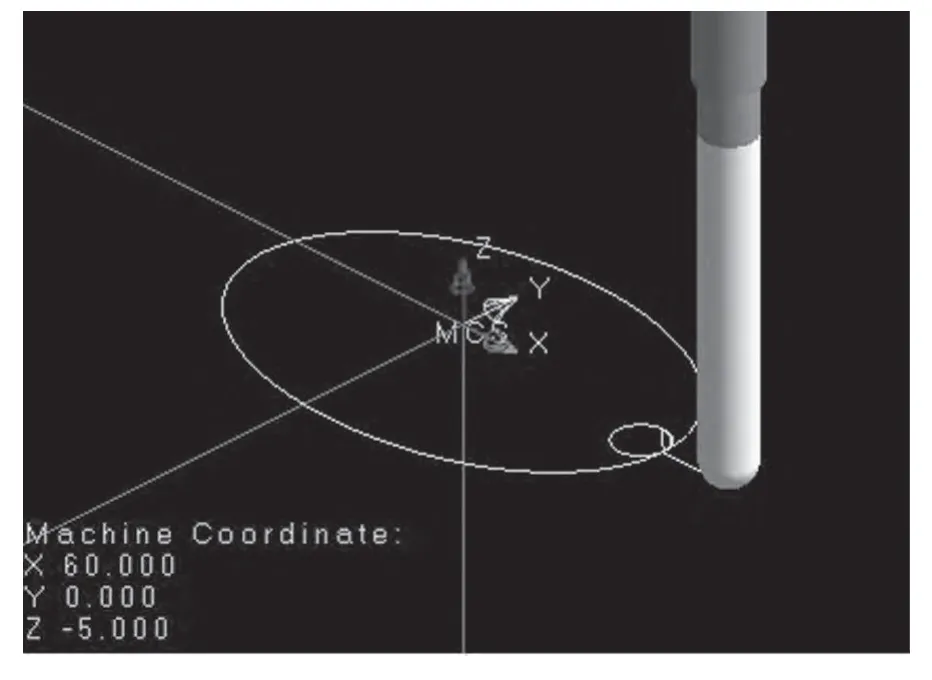
图5 仿真加工轨迹线

4 结束语

编制宏程序关键是建立好数学模型，确定好自变量及取值范围，列出变量表，然后画出流程图，理清思路就容易编制了。宏程序并非深不可测，它显著的特点是用变量进行赋值，很方便实现复杂的算术和逻辑运算，免去了大量的手工计算，让数控系统自动计算判别，减少自动编程每次都要画图的麻烦，宏程序特别适用于各种公式曲线零件编程，当加工条件改变时宏程序可以随时更改加工参数，以适应新的加工需求，宏程序充分体现模块化思维，一次编程多次受益，各种实例证明，宏程序加工非圆二次曲线类零件是一种高精度、高效率的加工方法。

［1］张喜江.加工中心宏程序应用案例［M］.北京：金盾出版社，2013.

［2］杨志红.浅谈宏程序的编程原理及应用［J］.机电工程技术，2010（12）：54-58.

［3］张宁菊.基于宏程序的内外螺纹的数控铣削加工［J］.机电工程技术，2013（1）：25-27.

［4］陈海舟.数控铣削加工宏程序及应用实例［M］.北京：机械工业出版社，2006.

［5］杜军.FANUC宏程序编程技巧与实例精解［M］.北京：化学工业出版社，2011.

［6］范文利，姜洪奎，张蔚波.CAXA2008制造工程师行业应用实例［M］.北京：机械工业出版社，2010.